Bài 9.44 trang 111 Toán 8 Tập 2 | Kết nối tri thức Giải Toán 8

❮ Bài trước Bài sau ❯

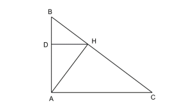
Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 4 cm. Gọi AH, HD lần lượt là các đường cao kẻ từ đỉnh A của tam giác ABC và đỉnh H của tam giác HAB.

Giải Toán 8 Bài tập cuối chương 9 (trang 110, 111) - Kết nối tri thức

Bài 9.44 trang 111 Toán 8 Tập 2: Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 4 cm. Gọi AH, HD lần lượt là các đường cao kẻ từ đỉnh A của tam giác ABC và đỉnh H của tam giác HAB.

a) Chứng minh rằng ΔHDA ∽ ΔAHC .

b) Tính độ dài các đoạn thẳng HA, HB, HC, HD.

Lời giải:

Bài 9.44 trang 110 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

a) Ta có $\hat{D A H} + \hat{H A C} = \hat{B A C} = 90 °$ $\hat{A C H} + \hat{H A C} = 90 °$ (do tam giác ACH vuông ở H).

Suy ra $\hat{D A H} = \hat{A C H}$ (cùng phụ với $\hat{H A C}$ ).

Tam giác HDA vuông tại D và tam giác AHC vuông tại H có $\hat{\hat{D A H} = \hat{A C H}}$ nên ΔHDA ∽ ΔAHC .

b) Áp dụng định lí Pythagore cho tam giác vuông ABC, ta có

BC² = AB² + AC² = 4² + 5² = 41.

Suy ra $B C = \sqrt{41}$ cm.

Diện tích tam giác ABC là: $S_{A B C} = \frac{A B \cdot A C}{2} = \frac{4 \cdot 5}{2} = 10$ (cm²).

Lại có $S_{A B C} = \frac{A H \cdot B C}{2}$ , do đó AH ∙ BC = 2 . 10 = 20, suy ra AH = $\frac{20}{B C}$ = $\frac{20}{\sqrt{41}}$ (cm).

Áp dụng định lí Pythagore cho tam giác ACH ta có AC² = AH² + CH².

Do đó, CH² = AC² – AH² = 4² – ${(\frac{20}{\sqrt{41}})}^{2} = \frac{256}{41}$ .

Suy ra $C H = \frac{16}{\sqrt{41}}$ (cm).

Vì ΔHDA ∽ ΔAHC nên $\frac{H D}{A H} = \frac{H A}{A C} \Rightarrow H D = \frac{A H^{2}}{A C} = \frac{\frac{400}{41}}{4} = \frac{100}{41}$ (cm).

Ta có BH = BC – HC = $\sqrt{41} - \frac{16}{\sqrt{41}} = \frac{25}{\sqrt{41}}$ (cm).

Lời giải bài tập Toán 8 Bài tập cuối chương 9 (trang 110, 111) hay, chi tiết khác:

Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯