Bài 9.45 trang 111 Toán 8 Tập 2 | Kết nối tri thức Giải Toán 8

❮ Bài trước Bài sau ❯

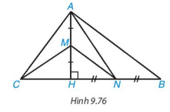
Cho tam giác ABC có đường cao AH. Biết AH = 12 cm, CH = 9 cm, BH = 16 cm. Lấy M, N lần lượt là trung điểm của AH, BH (H.9.76).

Giải Toán 8 Bài tập cuối chương 9 (trang 110, 111) - Kết nối tri thức

Bài 9.45 trang 111 Toán 8 Tập 2: Cho tam giác ABC có đường cao AH. Biết AH = 12 cm, CH = 9 cm, BH = 16 cm. Lấy M, N lần lượt là trung điểm của AH, BH (H.9.76).

a) Chứng minh rằng ABC là tam giác vuông tại A.

b) Chứng minh rằng MN ⊥ AC và CM ⊥ AN.

c) Tính diện tích tam giác AMN.

Bài 9.45 trang 110 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Lời giải:

a) Xét tam giác AHB vuông tại H, có:

AH² + HB² = AB² (định lý Pythagore)

Suy ra AB² = 12² + 16² = 400.

Suy ra AB = 20 cm.

Tương tự, có: AC² = AH² + CH² (áp dụng định lý Pythagore trong tam giác vuông AHC).

Suy ra AC² = 12² + 9² = 225.

Suy ra AC = 15 cm.

Có BC = CH + BH = 9 + 16 = 25 cm.

Trong tam giác ABC, nhận thấy AB² + AC² = BC² (do 20² + 15² = 25² = 625).

Suy ra tam giác ABC vuông tại A (định lí Pythagore đảo).

b) Xét tam giác AHB có:

M là trung điểm của AH

N là trung điểm của BH

Suy ra MN là đường trung bình của tam giác AHB.

Do đó, MN // AB. Mà AB ⊥ AC (vì tam giác ABC vuông tại A).

Suy ra MN ⊥ AC.

Xét ΔACN có AH ⊥ CN (gt), MN ⊥ AC (cmt), AH ∩ MN = {M}.

Vậy M là trực tâm của ΔACN, do đó CM ⊥ AN

c) Ta có S_AMN = $\frac{A M \cdot H N}{2} = \frac{\frac{A H}{2} \cdot \frac{B H}{2}}{2} = \frac{A H \cdot B H}{8} = \frac{12 \cdot 16}{8} = 24$ (cm²).

Lời giải bài tập Toán 8 Bài tập cuối chương 9 (trang 110, 111) hay, chi tiết khác:

Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯