Bài 6 trang 89 Toán 9 Tập 1 Chân trời sáng tạo

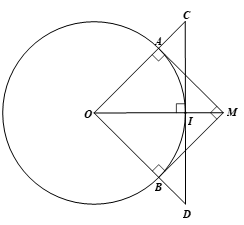
Cho đường tròn (O; 5 cm) điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A, B là hai tiếp điểm) vuông góc với nhau tại M.

Giải Toán 9 Bài 2: Tiếp tuyến của đường tròn - Chân trời sáng tạo

Bài 6 trang 89 Toán 9 Tập 1: Cho đường tròn (O; 5 cm) điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A, B là hai tiếp điểm) vuông góc với nhau tại M.

a) Tính độ dài của MA và MB.

b) Qua giao điểm I của đoạn thẳng MO và đường tròn (O), vẽ một tiếp tuyến cắt OA, OB lần lượt tại C, D. Tính độ dài của CD.

Lời giải:

Vì MA, MB lần lượt là hai tiếp tuyến của đường tròn (O) tại A, B nên MA ⊥ OA và MB ⊥ OB hay $\widehat{OAM}=90°;\widehat{OBM}=90°.$

Xét tứ giác OAMB có: $\widehat{OAM}=90°;\widehat{OBM}=90°;\widehat{AMB}=90°$(do MA ⊥ MB).

Do đó tứ giác OAMB là hình chữ nhật.

Lại có OA = OB = 5 cm (do A, B nằm trên đường tròn (O; 5 cm)).

Suy ra hình chữ nhật OAMB là hình vuông, nên MA = MB = OA = OB = 5 cm.

b) Vì OAMB là hình vuông nên $\widehat{AOB}=90°$ và OM là tia phân giác của góc AOB.

Do đó $\widehat{AOM}=\widehat{BOM}=\frac{1}{2}\widehat{AOB}=\frac{1}{2}\cdot 90°=45°.$

Vì CD là tiếp tuyến của đường tròn (O) tại I nên CD ⊥ OI.

Xét ∆OCI vuông tại I, ta có: $CI=OI\cdot \tan \widehat{COI}=5\cdot \tan 45°=5\text{ (cm).}$

Xét ∆ODI vuông tại I, ta có: $DI=OI\cdot \tan \widehat{CDOI}=5\cdot \tan 45°=5\text{ (cm).}$

Vậy CD = CI + DI = 5 + 5 = 10 (cm).

Lời giải bài tập Toán 9 Bài 2: Tiếp tuyến của đường tròn hay, chi tiết khác:

• Khởi động trang 83 Toán 9 Tập 1: Hãy mô tả các vị trí của Mặt Trời so với đường chân trời ở các thời điểm Mặt Trời lặn ....

• Khám phá 1 trang 83 Toán 9 Tập 1: Nêu nhận xét về số điểm chung của đường thẳng a và đường tròn (O) trong mỗi hình sau ....

• Thực hành 1 trang 85 Toán 9 Tập 1: Cho đường tròn (J; 5 cm) và đường thẳng c. Gọi K là chân đường vuông góc vẽ từ J xuống c ....

• Vận dụng 1 trang 85 Toán 9 Tập 1: Một diễn viên xiếc đi xe đạp một bánh trên sợi dây cáp căng được cố định ở hai đầu dây ....

• Khám phá 2 trang 85 Toán 9 Tập 1: Cho điểm A nằm trên đường tròn (O; R), đường thẳng d đi qua A và vuông góc với OA ....

• Thực hành 2 trang 86 Toán 9 Tập 1: Cho tam giác ABC có đường cao AH (Hình 8). Tìm tiếp tuyến của đường tròn (A; AH) tại H ....

• Vận dụng 2 trang 86 Toán 9 Tập 1: Một diễn viên xiếc đi xe đạp trên một sợi dây cáp căng (Hình 9). Ta coi sợi dây là tiếp tuyến của mỗi bánh xe ....

• Khám phá 3 trang 87 Toán 9 Tập 1: Cho đường tròn (O) và hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại điểm A (Hình 10) ....

• Thực hành 3 trang 87 Toán 9 Tập 1: Cho điểm M nằm ngoài đường tròn (I; 6 cm) và ME, MF là hai tiếp tuyến của đường tròn này tại E và F ....

• Thực hành 4 trang 88 Toán 9 Tập 1: Tìm giá trị của x trong Hình 12 ....

• Vận dụng 3 trang 88 Toán 9 Tập 1: Bánh đà của một động cơ được thiết kế có dạng là một đường tròn tâm O, bán kính 15 cm được kéo bởi một dây curoa ....

• Bài 1 trang 88 Toán 9 Tập 1: Trong Hình 14, MB, MC lần lượt là tiếp tuyến của đường tròn (O) tại B, C; $\widehat{\text{COB}}=130°.$ ....

• Bài 2 trang 88 Toán 9 Tập 1: Quan sát Hình 15. Biết AB, AC lần lượt là tiếp tuyến của đường tròn (O) tại B, C. Tính giá trị của x ....

• Bài 3 trang 89 Toán 9 Tập 1: Trong Hình 16, AB = 9, BC = 12, AC = 15 và BC là đường kính của đường tròn (O) ....

• Bài 4 trang 89 Toán 9 Tập 1: Cho tam giác ABC có đường tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác ....

• Bài 5 trang 89 Toán 9 Tập 1: Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho AC = R. Gọi I là trung điểm của dây AC ....

• Bài 7 trang 89 Toán 9 Tập 1: Cho đường tròn (O), điểm M nằm ngoài (O) sao cho MA và MB là hai tiếp tuyến ....

• Bài 8 trang 89 Toán 9 Tập 1: Trong Hình 18, AB là tiếp tuyến của đường tròn (O) tại B ....