Vận dụng 3 trang 88 Toán 9 Tập 1 Chân trời sáng tạo

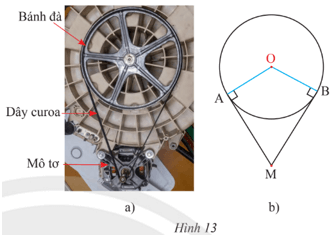
Bánh đà của một động cơ được thiết kế có dạng là một đường tròn tâm O, bán kính 15 cm được kéo bởi một dây curoa. Trục của mô tơ truyền lực được biểu diễn bởi điểm M (Hình 13). Cho biết khoảng cách OM là 35 cm.

Giải Toán 9 Bài 2: Tiếp tuyến của đường tròn - Chân trời sáng tạo

Vận dụng 3 trang 88 Toán 9 Tập 1: Bánh đà của một động cơ được thiết kế có dạng là một đường tròn tâm O, bán kính 15 cm được kéo bởi một dây curoa. Trục của mô tơ truyền lực được biểu diễn bởi điểm M (Hình 13). Cho biết khoảng cách OM là 35 cm.

a) Tính độ dài của hai đoạn dây curoa MA và MB (kết quả làm tròn đến hàng phần mười).

b) Tính số đo $\widehat{\text{AMB}}$ tạo bởi hai tiếp tuyến AM, BM và số đo $\widehat{\text{AOB}}$ (kết quả làm tròn đến phút).

Lời giải:

a) Ta có MA, MB lần lượt là hai tiếp tuyến của đường tròn (O; 15 cm) tại A, B và cắt nhau tại M nên MA ⊥ OA, MB ⊥ OB và MA = MB.

Xét ∆OAM vuông tại A, theo định lí Pythagore ta có: OM² = OA² + MA².

Suy ra MA² = OM² – OA² = 35² – 15² = 1 000.

Do đó $MA=\sqrt{1000}\approx \mathrm{31,6}\text{ (cm).}$

Vậy MA = MB ≈ 31,6 cm.

b) Xét ∆OAM vuông tại A, ta có: $\sin \widehat{AMO}=\frac{OA}{OM}=\frac{15}{35}=\frac{3}{7}.$

Suy ra $\widehat{AMO}\approx 25°{23}^{\text{'}}.$

Vì MA, MB là hai tiếp tuyến của đường tròn (O; 15 cm) cắt nhau tại M nên MA là tia phân giác của góc AMB.

Do đó $\widehat{AMB}=2\widehat{AMO}\approx 2\cdot 25°{23}^{\text{'}}=50°{46}^{\text{'}}.$

Xét tứ giác OAMB có: $\widehat{OAM}+\widehat{AMB}+\widehat{OBM}+\widehat{AOB}=360°$(tổng các góc của một tứ giác).

Suy ra $\widehat{AOB}=360°-\left(\widehat{OAM}+\widehat{AMB}+\widehat{OBM}\right)$

Do đó $\widehat{AOB}\approx 360°-\left(90°+50°{46}^{\text{'}}+90°\right)=360°-230°{46}^{\text{'}}=129°{14}^{\text{'}}.$

Lời giải bài tập Toán 9 Bài 2: Tiếp tuyến của đường tròn hay, chi tiết khác:

• Khởi động trang 83 Toán 9 Tập 1: Hãy mô tả các vị trí của Mặt Trời so với đường chân trời ở các thời điểm Mặt Trời lặn ....

• Khám phá 1 trang 83 Toán 9 Tập 1: Nêu nhận xét về số điểm chung của đường thẳng a và đường tròn (O) trong mỗi hình sau ....

• Thực hành 1 trang 85 Toán 9 Tập 1: Cho đường tròn (J; 5 cm) và đường thẳng c. Gọi K là chân đường vuông góc vẽ từ J xuống c ....

• Vận dụng 1 trang 85 Toán 9 Tập 1: Một diễn viên xiếc đi xe đạp một bánh trên sợi dây cáp căng được cố định ở hai đầu dây ....

• Khám phá 2 trang 85 Toán 9 Tập 1: Cho điểm A nằm trên đường tròn (O; R), đường thẳng d đi qua A và vuông góc với OA ....

• Thực hành 2 trang 86 Toán 9 Tập 1: Cho tam giác ABC có đường cao AH (Hình 8). Tìm tiếp tuyến của đường tròn (A; AH) tại H ....

• Vận dụng 2 trang 86 Toán 9 Tập 1: Một diễn viên xiếc đi xe đạp trên một sợi dây cáp căng (Hình 9). Ta coi sợi dây là tiếp tuyến của mỗi bánh xe ....

• Khám phá 3 trang 87 Toán 9 Tập 1: Cho đường tròn (O) và hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại điểm A (Hình 10) ....

• Thực hành 3 trang 87 Toán 9 Tập 1: Cho điểm M nằm ngoài đường tròn (I; 6 cm) và ME, MF là hai tiếp tuyến của đường tròn này tại E và F ....

• Thực hành 4 trang 88 Toán 9 Tập 1: Tìm giá trị của x trong Hình 12 ....

• Bài 1 trang 88 Toán 9 Tập 1: Trong Hình 14, MB, MC lần lượt là tiếp tuyến của đường tròn (O) tại B, C; $\widehat{\text{COB}}=130°.$ ....

• Bài 2 trang 88 Toán 9 Tập 1: Quan sát Hình 15. Biết AB, AC lần lượt là tiếp tuyến của đường tròn (O) tại B, C. Tính giá trị của x ....

• Bài 3 trang 89 Toán 9 Tập 1: Trong Hình 16, AB = 9, BC = 12, AC = 15 và BC là đường kính của đường tròn (O) ....

• Bài 4 trang 89 Toán 9 Tập 1: Cho tam giác ABC có đường tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác ....

• Bài 5 trang 89 Toán 9 Tập 1: Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho AC = R. Gọi I là trung điểm của dây AC ....

• Bài 6 trang 89 Toán 9 Tập 1: Cho đường tròn (O; 5 cm) điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB ....

• Bài 7 trang 89 Toán 9 Tập 1: Cho đường tròn (O), điểm M nằm ngoài (O) sao cho MA và MB là hai tiếp tuyến ....

• Bài 8 trang 89 Toán 9 Tập 1: Trong Hình 18, AB là tiếp tuyến của đường tròn (O) tại B ....