Bài 7 trang 56 Toán 9 Tập 1 Chân trời sáng tạo

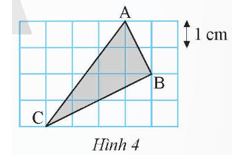
Tam giác ABC được vẽ trên lưới ô vuông như Hình 4. Tính diện tích và chu vi của tam giác ABC.

Giải Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

Bài 7 trang 56 Toán 9 Tập 1: Tam giác ABC được vẽ trên lưới ô vuông như Hình 4. Tính diện tích và chu vi của tam giác ABC.

Lời giải:

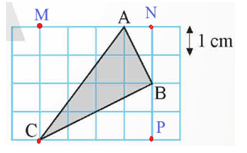
Gọi các điểm M, N, P như hình vẽ.

Bài 7 trang 56 Toán 9 Tập 1 Chân trời sáng tạo

Độ dài mỗi cạnh của lưới ô vuông bằng 1 cm.

Hình vuông MNPC chứa tam giác ABC có độ dài mỗi cạnh bằng 4 cm.

Diện tích hình vuông MNPC là: S_MNPC = 4² = 16 (cm²).

• Xét tam giác AMC có AM = 3 cm, CM = 4 cm.

Áp dụng định lí Pythagore, ta có: AC²= AM² + CM² = 3² + 4² = 25.

Suy ra AC = 5 cm.

Diện tích tam giác AMC là: $S_{A M C} = \frac{1}{2} . 3 . 4 = 6 (c m^{2})$ .

• Xét tam giác ABN có AN = 1 cm, BN = 2 cm.

Áp dụng định lí Pythagore, ta có: AB²= AN² + BN² = 1² + 2² = 5.

Suy ra $A B = \sqrt{5} c m$

Diện tích tam giác ABN là: $S_{A B N} = \frac{1}{2} . 1 . 2 = 1 (c m^{2})$ .

• Xét tam giác BCP có NP = 2 cm, CP = 4 cm.

Áp dụng định lí Pythagore, ta có: BC²= NP² + CP² = 2² + 4² = 20.

Suy ra $B C = \sqrt{20} = 2 \sqrt{5} (c m)$

Diện tích tam giác BCP là: $S_{B C P} = \frac{1}{2} . 2 . 4 = 4 (c m^{2})$ .

Khi đó, chu vi tam giác ABC là: AB + BC + AC = $\sqrt{5} + 2 \sqrt{5} + 5 = 5 + 3 \sqrt{5}$

Diện tích tam giác ABC là:

S_ABC = S_MNPC – S_AMC– S_ABN– S_BCP= 16 – 6 – 1 – 4 = 5 (cm²).

Vậy chu vi tam giác ABC là $5 + 3 \sqrt{5} (c m)$ và diện tích tam giác ABC là 5 cm².

Lời giải bài tập Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai hay, chi tiết khác: