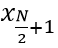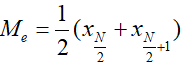Các dạng bài tập Thống kê chọn lọc có lời giải - Toán lớp 10

---

Các dạng bài tập Thống kê chọn lọc có lời giải

Với Các dạng bài tập Thống kê chọn lọc có lời giải Toán lớp 10 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Thống kê từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

Tổng hợp lý thuyết chương Thống kê

• Lý thuyết Bảng phân bố tần số và tần suất Xem chi tiết
• Lý thuyết Biểu đồ Xem chi tiết
• Lý thuyết Số trung bình cộng. Số trung vị. Mốt Xem chi tiết
• Lý thuyết Phương sai và độ lệch chuẩn Xem chi tiết
• Lý thuyết Tổng hợp chương Thống kê Xem chi tiết

Lý thuyết Biểu đồ

1.Biểu đồ tần suất hình cột:

Cách vẽ:

• Vẽ hai đường thẳng vuông góc. Trên đường thẳng nằm ngang (dùng làm trục số) ta đánh dáu các khoảng xác định lớp.

• Tại mỗi khoảng ta dựng lên một hình cột chữ nhật, với đáy là khoảng đó, còn chiều cao bằng tần suất của lớp mà khoảng đó xác định

2. Đường gấp khúc tần suất

Cách vẽ: Ta vẽ hai đường thẳng vuông góc ( như hình vễ biểu đồ hình cột). Trên mặt phẳng tọa độ xác định các điểm (c_i+1; f_i+1), i = 1, 2, 3,…, n sau đó vẽ các đoạn thẳng nối các điểm (ci, fi) với các điểm (c_i+1; f_i+1), i = 1, 2, 3,…, n ta thu được một đường gấp khúc. Đường gấp khúc này gọi là đường gấp khúc tần suất.

3. Biểu đồ hình quạt:

Cách vẽ: vẽ hình tròn, chia hình tròn thành những hình quạt, mỗi lớp tương ứng với một hình quạt mà diện tích của nó tỉ lệ với tần suất của lớp đó.

4. Ví dụ

Dạng 1: Vẽ biểu đồ tần suất hình cột

Phương pháp:

- Vẽ hai đường thẳng vuông góc

- Trên đường thẳng nằm ngang ( dùng làm trục số) ta đánh dấu các khoảng xác định lớp

- Tại mỗi khoảng ta dựng một cột hình chữ nhật với đáy là khoảng đó còn chiều cao bằng tần số hoặc tần suất của lớp mà khoảng đó xác định

- Hình thu được là biểu đồ hình cột tần số hoặc tần suất

Bài tập 1: thống kê điểm toán của 40 học sinh của một lớp người ta thu được mẫu số liệu ban đầu như sau:

5	6	6	5	7	1	2	4	6	9
4	5	7	5	6	8	10	5	5	7
2	1	3	3	6	4	6	5	5	9
8	7	2	1	8	6	4	4	6	5

a) Hãy lập bảng phân bố tần số - tần suất ghép lớp với các lớp như sau:

[1; 2]; [3; 4]; [5; 6]; [7; 8]; [9; 10]

b) Vẽ biểu đồ hình cột tần số

Lời giải

a) Bảng phân bố tần số - tần suất

Điểm toán	Tần số	Tần suất %
[1; 2]	6	15
[3; 4]	7	17.5
[5; 6]	17	42.5
[7; 8]	7	17.5
[9; 10]	3	7.5
	N = 40	100%

Biểu đồ:

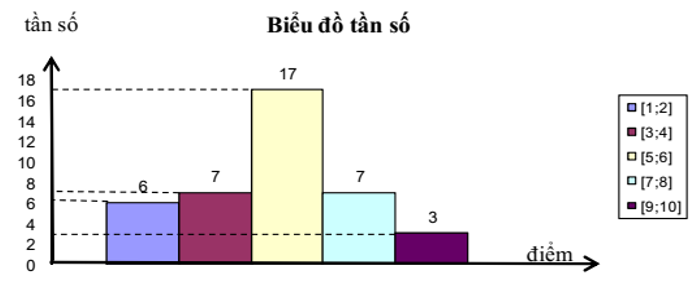
Dạng 2: Vẽ biểu đồ đường gấp khúc tần số - tần suất ghép lớp

Phương pháp:

- Vẽ hai đường thẳng vuông góc làm hai trục

- Trên trục nằm ngang ta đánh dấu các điểm A₁, A₂,…, A_m, với A_i là trung điểm, của nửa khoảng xác định lớp thứ I ( i=1; 2; 3;…; m)

- Tại mỗi điểm Ai ta dựng đoạn thẳng A_iM_i vuông góc với trục nằm ngang và có tốc độ dài bằng tần số thứ I ( tức ni)

- Vẽ các đoạn thẳng M₁M₂, M₂M₃, M₃M₄,…, M_m-1M ta được đường gấp khúc tần số

- Nếu độ dài các đoạn thẳng AiMi được lấy bằng tần suất của lớp thứ I ( tức fi) thì khi vẽ các đoạn thẳng M₁M₂, M₂M₃, M₃M₄,…, M_m-1M ta được đường gấp khúc tần suất

Bài tập 2: thống kê điểm toán của 40 học sinh của một lớp người ta thu được mẫu số liệu ban đầu như sau:

5	6	6	5	7	1	2	4	6	9
4	5	7	5	6	8	10	5	5	7
2	1	3	3	6	4	6	5	5	9
8	7	2	1	8	6	4	4	6	5

a) Hãy lập bảng phân bố tần số - tần suất ghép lớp với các lớp như sau:

[1; 2]; [3; 4]; [5; 6]; [7; 8]; [9; 10]

b) Vẽ biểu đồ đường gấp khúc tần suất

Lời giải

a) Bảng phân bố tần số - tần suất

Điểm toán	Tần số	Tần suất %
[1; 2]	6	15
[3; 4]	7	17.5
[5; 6]	17	42.5
[7; 8]	7	17.5
[9; 10]	3	7.5
	N=40	100%

b) Biểu đồ đường gấp khúc

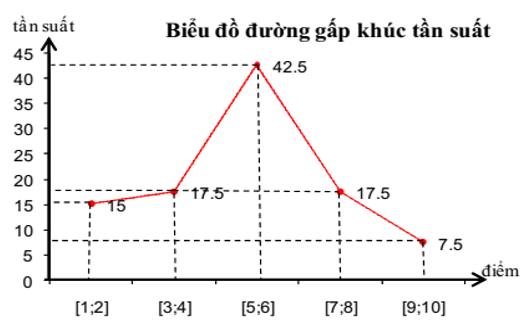Dạng 3: Vẽ biểu đồ hình quạt

Phương pháp:

- Vẽ hình tròn

- Chia hình tròn thành các hình quạt ứng với các lớp. mỗi lớp được vẽ tương ứng với một hình quạt mà diện tích của nó tỉ lệ với tần suất của lớp đó, hoặc tỉ lệ với tỉ số phần trăm của cơ cấu của mỗi thành phần

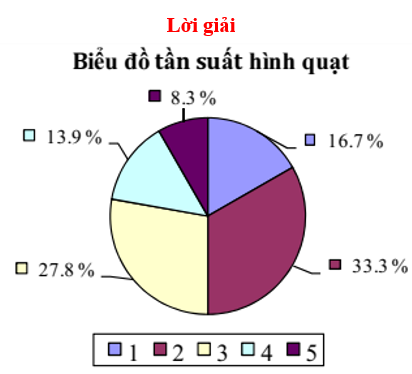
Bài tập 3: vẽ biểu đồ hình quạt thống kê chiều cao của 36 học sinh( đv:cm) nam của một trường trung học phổ thông được cho bởi bảng phân bố tần số - tần suất sau:

Nhóm	Lớp	Tần số	Tần suất
1	[160; 162]	6	16.7
2	[163; 165]	12	33.3
3	[166; 168]	10	27.8
4	[169; 171]	5	13.9
5	[172; 174]	3	8.3
		N=36	100%

Lý thuyết Số trung bình cộng. Số trung vị. Mốt

Để thu được thông tin quan trọng từ các số liệu thống kê, người ta sử dụng những số đặc trưng như: số trung bình cộng, số trung vị, mốt, phương sai, dộ lệch chuẩn. Các số đạc trưng này phản ánh những khía cạnh khác nhau của dấu hiệu điều tra.

1. Số trung bình cộng : Kí hiệu: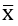

Bảng phân bố tần suất và tần số

Tên dữ liệu	Tần số	Tần suất (%)
x1 x2 . xk	n1 n2 . nk	f1 f2 . fk
Cộng	n = n1 + … + nk	100%

Trung bình cộng của các số liệu thống kê được tính theo công thức:

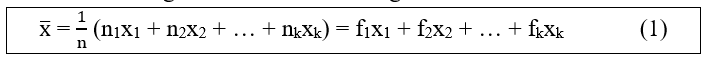
Trường hợp Bảng phân bố tần suất và tần số ghép lớp

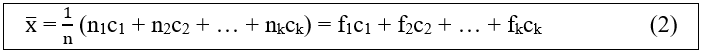
c_i, f_i, n_i là giá trị đại diện của lớp thứ i.

Ý nghĩa của số trung bình:

Số trung bình của mẫu số liệu được dùng làm đại diện cho các số liệu của mẫu. Nó là một số đặc trưng quan trọng của mẫu số liệu.

Ví dụ 1: Một nhà thực vật học đo chiều dài của 74 chiếc lá cây và thu được số liệu sau ( đơn vị mm)

Lớp	Giá trị đại diện	Tần số
[5,45 ; 5,85) [5,85 ; 6,25) [6,25 ; 6,65) [6,65 ; 7,05) [7,05 ; 7,45) [7,45 ; 7,85) [7,85 ; 8,25)	5,65 6,05 6,45 6,85 7,25 7,65 8,05	5 9 15 19 16 8 2
		N = 74

Khi đó chiều dài trung bình của 74 chiếc lá này là :

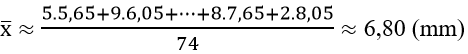
Ví dụ 2: Một nhóm 11 học sinh tham gia một kì thi. Số điểm thi của 11 học sinh đó được sắp xếp từ thấp đến cao như sau: (thang điểm 100): 0 ; 0 ; 63 ; 65 ; 69 ; 70 ; 72 ; 78 ; 81 ; 85 ; 89.

Điểm trung bình là:

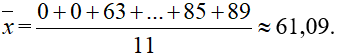
Quan sát dãy điểm trên, ta thấy hầu hết (9 em) trong nhóm có số điểm vượt điểm trung bình. Như vậy, điểm trung bình này không phản ứng đúng trình độ trung bình của nhóm.

2. Số trung vị:Kí hiệu: M_e

Khi các số liệu trong mẫu có sự chênh lệnh rất lớn đối với nhau thì số trung bình khó có thể đại diện cho các số liệu trong mẫu. Có một chỉ số khác thích hợp hơn trong trường hợp này. Đó là số trung vị.

Định nghĩa: Giả sử ta có dãy n số liệu được sắp xếp thành dãy không giảm (hoặc không tăng). Khi đó, số trung vị (của các số liệu thống kê đã cho) kí hiệu là M_e là :

+ Số đứng giữa dãy nếu số phần tử N lẻ: M_e =

+ Trung bình cộng của hai số đứng giữa dãy nếu số phần tử N chẵn:

Ví dụ 1: Điểm thi toán của 9 học sinh như sau: 1; 1; 3; 6; 7; 8; 8; 9; 10

Ta có M_e = 7

Ví dụ 2: Số điểm thi toán của 4 học sinh như sau: 1; 2,5; 8; 9,5

Ta có M_e = 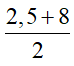= 5,25

3. Mốt: Kí hiệu: M_o

Mốt của bảng phân bố tần số là giá trị (x_i) có tần số (n_i ) lớn nhất và được kí hiệu là M_o.

Chú ý: Có hai giá trị tần số bằng nhau và lớn hơn tần số các giá trị khác thì ta nói trường hợp này có hai Mốt, kí hiệu M_o¹,M_o² .

Ví dụ :Một cửa hàng bán 6 loại quạt với giá tiền là 100, 150, 300, 350, 400, 500 (nghìn đồng). Số quạt cửa hàng bán ra trong mùa hè vừa qua được thống kê trong bảng tần số sau:

Giá tiền	100	150	300	350	400	500
Số quạt bán được	256	353	534	300	534	175

Mốt M_o = 300

4. Chọn đại diện cho các số liệu thống kê:

a) Trường hợp các số liệu thông kê cùng loại và số lượng thống kê đủ lớn (n ≥ 30) thì ta ưu tiên chọn số trung bình làm đại diện cho các số liệu thống kê ( về quy mô và độ lớn).

b) Trường hợp không tính được giá trị trung bình thì ta chọn số trung vị hoặc mốt làm đại diện cho các số liệu thống kê ( về quy mô và độ lớn).

c) Không nên dùng số trung bình để đại diện cho các số liệu thống kê trong các trường hợp sau (có thể dùng số trung vị hoặc mốt):

+ Số các số liệu thống kê quá ít (n ≤ 10).

+ Giữa các số liệu thống kê có sự chênh lệc quá lớn.

+ Đường gấp khúc tần suất không đối xứng, (và nhiều trường hợp khác)