Các dạng bài tập Tích vô hướng của hai vectơ chọn lọc có lời giải - Toán lớp 10

---

Các dạng bài tập Tích vô hướng của hai vectơ chọn lọc có lời giải

Với Các dạng bài tập Tích vô hướng của hai vectơ chọn lọc có lời giải Toán lớp 10 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tích vô hướng của hai vectơ từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

Tổng hợp lý thuyết chương Tích vô hướng của hai vectơ và ứng dụng

• Lý thuyết Giá trị lượng giác của một góc bất kì từ 0^o đến 180^o Xem chi tiết
• Lý thuyết Tích vô hướng của hai vectơ Xem chi tiết
• Lý thuyết Các hệ thức lượng trong tam giác và giải tam giác Xem chi tiết
• Lý thuyết Tổng hợp chương Tích vô hướng của hai vectơ và ứng dụng Xem chi tiết

Các dạng bài tập chương Tích vô hướng và ứng dụng

• Cách tính độ dài vecto, khoảng cách giữa hai điểm trong hệ tọa độ cực hay, chi tiết Xem chi tiết
• Công thức, cách tính góc giữa hai vecto cực hay, chi tiết Xem chi tiết
• Cách chứng minh Hai vecto vuông góc cực hay, chi tiết Xem chi tiết
• Tìm m để góc giữa hai vecto bằng một số cho trước cực hay (45 độ, góc nhọn, góc tù) Xem chi tiết
• Cách giải bài tập về Định lí Cô-sin trong tam giác cực hay, chi tiết Xem chi tiết
• Cách giải bài tập về Định lí Sin trong tam giác cực hay, chi tiết Xem chi tiết
• Công thức, cách tính độ dài đường trung tuyến cực hay, chi tiết Xem chi tiết
• Công thức, cách tính Diện tích tam giác cực hay, chi tiết Xem chi tiết
• Bài tập Công thức Heron tính diện tích tam giác cực hay, chi tiết Xem chi tiết
• Cách làm bài tập Giải tam giác lớp 10 cực hay, chi tiết Xem chi tiết
• Cách tính bán kính đường tròn ngoại tiếp tam giác cực hay, chi tiết Xem chi tiết
• Cách tính bán kính đường tròn nội tiếp tam giác cực hay, chi tiết Xem chi tiết

Cách chứng minh Hai vecto vuông góc

A. Phương pháp giải

Phương pháp 1: Sử dụng định nghĩa

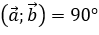
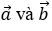
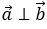
Nếu thì hai vectơ vuông góc với nhau, kí hiệu .

Phương pháp 2: Sử dụng tính chất của tích vô hướng và áp dụng trong hệ tọa độ

Cho .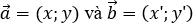

Khi đó:

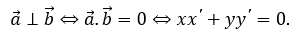
B. Ví dụ minh họa

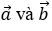
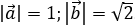
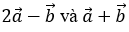
Ví dụ 1: Cho hai vectơ vuông góc với nhau và . Chứng minh hai vectơ vuông góc với nhau.

Hướng dẫn giải:

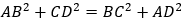
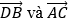
Ví dụ 2: Cho tứ giác ABCD có . Chứng minh hai vectơ vuông góc.

Hướng dẫn giải:

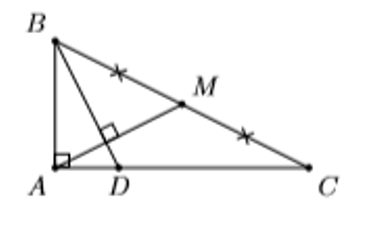
Ví dụ 3: Cho tam giác ABC vuông tại A có AB = a, AC = 2a. Gọi M là trung điểm của BC và điểm D bất kỳ thuộc cạnh AC. Tính AD theo a để BD ⊥ AM.

Hướng dẫn giải:

Tìm m để góc giữa hai vecto bằng một số cho trước (45 độ, góc nhọn, góc tù)

A. Phương pháp giải

Các bước làm bài

B. Ví dụ minh họa

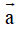
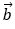
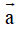
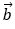
Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho hai vectơ = (3;m) và = (1;7). Xác định m để góc giữa hai vectơ và là 45°.

Hướng dẫn giải:

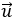
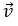
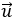
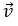
Ví dụ 2: Trong mặt phẳng tọa độ Oxy, cho hai vectơ = (-1;1) và = (m;⁡2). Tìm m để góc giữa hai vectơ và là 135°.

Hướng dẫn giải:

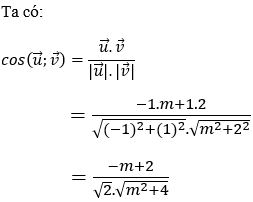
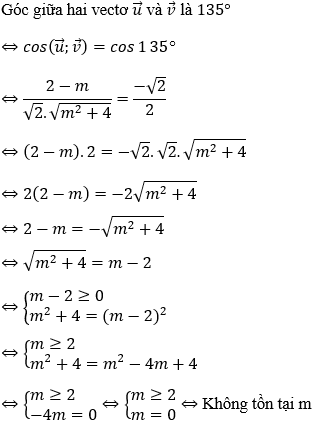
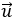
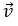
Vậy không tồn tại m để góc giữa hai vectơ và là 135°.

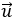
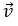
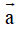
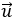
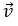
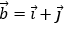
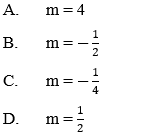
Ví dụ 3: Trong mặt phẳng tọa độ Oxy cho hai vectơ = (4;1) và vectơ = (1;4). Tìm m để vectơ =m. + tạo với vectơ một góc 45°.

Hướng dẫn giải:

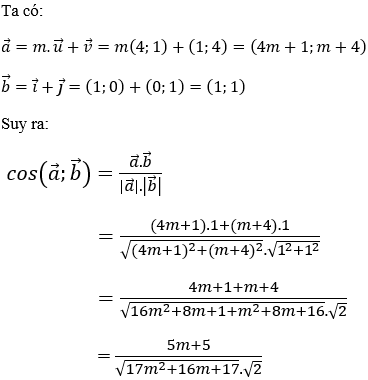
Đáp án C

Công thức, cách tính độ dài đường trung tuyến

A. Phương pháp giải

Áp dụng công thức tính độ dài đường trung tuyến:

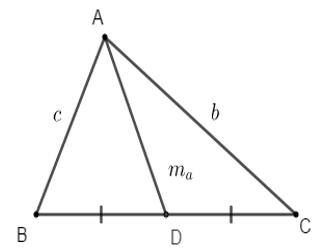
Cho tam giác ABC có các cạnh BC = a, CA = b và AB = c. Gọi m_a; m_b; m_c là độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B và C của tam giác. Khi đó

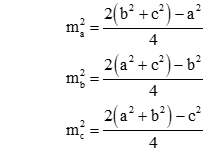
B. Ví dụ minh họa

Ví dụ 1: Cho tam giác ABC có BC = a = 10 cm, CA = b = 8 cm, AB = c = 7 cm. Tính độ dài các đường trung tuyến của tam giác ABC.

Hướng dẫn giải:

Gọi độ dài trung tuyến từ các đỉnh A, B, C của tam giác ABC lần lượt là m_a; m_b; m_c.

Áp dụng công thức trung tuyến ta có:

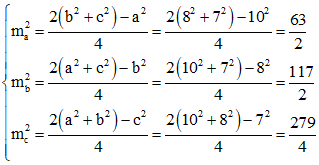
Vì độ dài các đường trung tuyến (là độ dài đoạn thẳng) nên nó luôn dương, do đó:

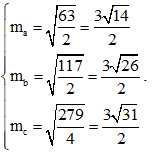
Ví dụ 2: Cho tam giác ABC, có BC = a, CA = b và AB = c. Chứng minh rằng nếu b² + c² = 5a² thì hai trung tuyến kẻ từ B và C của tam giác vuông góc với nhau.

Hướng dẫn giải:

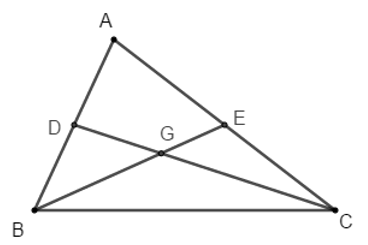
Gọi D và E lần lượt là trung điểm của AB và AC, G là trọng tâm tam giác ABC.

Đặt BE = m_b, CD = m_c

Áp dụng công thức trung tuyến trong tam giác ABC ta có:

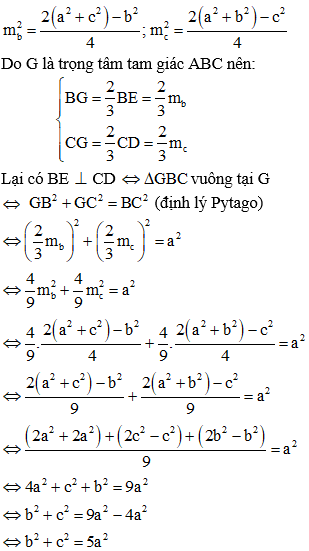
Vậy b² + c² = 5a² thì hai trung tuyến kẻ từ B và C của tam giác vuông góc với nhau. (đpcm)

Ví dụ 3: Cho tam giác ABC có AB = 3, BC = 5 và độ dài đường trung tuyến 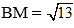. Độ dài AC là:

Hướng dẫn giải:

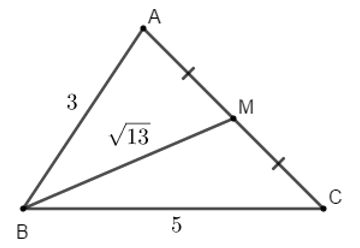
BM là trung tuyến của tam giác ABC, áp dụng công thức trung tuyến ta có:

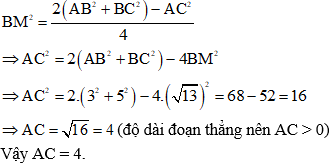
Đáp án B