Các dạng bài tập Phương pháp tọa độ trong mặt phẳng chọn lọc có lời giải - Toán lớp 10

Các dạng bài tập Phương pháp tọa độ trong mặt phẳng chọn lọc có lời giải

Với Các dạng bài tập Phương pháp tọa độ trong mặt phẳng chọn lọc có lời giải Toán lớp 10 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Phương pháp tọa độ trong mặt phẳng từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

Các dạng bài tập Phương pháp tọa độ trong mặt phẳng chọn lọc có lời giải

Tổng hợp lý thuyết chương Phương pháp tọa độ trong mặt phẳng

Chủ đề: Phương trình đường thẳng

Chủ đề: Phương trình đường tròn

Chủ đề: Phương trình đường elip

Cách tìm vecto pháp tuyến của đường thẳng

A. Phương pháp giải

Cho đường thẳng d: ax + by + c= 0. Khi đó, một vecto pháp tuyến của đường thẳng d là n→( a;b).

Một điểm M(x₀; y₀) thuộc đường thẳng d nếu: ax₀ + by₀ + c = 0.

B. Ví dụ minh họa

Ví dụ 1: Vectơ pháp tuyến của đường thẳng 2x- 3y+ 7= 0 là :

A. n₄→ = (2; -3) B. n₂→ = (2; 3) C. n₃→ = (3; 2) D. n₁→ = (-3; 2)

Lời giải

Cho đường thẳng d: ax + by + c= 0. Khi đó; đường thẳng d nhận vecto ( a; b) làm VTPT.

⇒ đường thẳng d nhận vecto n→( 2;-3) là VTPT.

Chọn A.

Ví dụ 2. Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng song song với trục Ox?

A. n→( 1; 1) B. n→( 0; -1) C. n→(1; 0) D. n→( -1; 1)

Lời giải

Đường thẳng song song với Ox có phương trình là : y + m= 0 ( với m ≠ 0) .

Đường thẳng này nhận vecto n→( 0; 1) làm VTPT.

Suy ra vecto n'→( 0; -1 ) cũng là VTPT của đường thẳng( hai vecto n→ và n'→ là cùng phương) .

Chọn B.

Ví dụ 3: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng song song với trục Oy?

A. n→( 1; 1) B. n→( 0; -1) C. n→(2; 0) D. n→( -1; 1)

Lời giải

Đường thẳng song song với Oy có phương trình là : x + m= 0 ( với m ≠ 0) .

Đường thẳng này nhận vecto n→(1;0) làm VTPT.

Suy ra vecto n'→( 2; 0 ) cũng là VTPT của đường thẳng( hai vecto n→ và n'→ là cùng phương) .

Chọn D.

Cách viết phương trình tổng quát của đường thẳng

A. Phương pháp giải

* Để viết phương trình tổng quát của đường thẳng d ta cần xác định :

- Điểm A(x₀; y₀) thuộc d

- Một vectơ pháp tuyến n→( a; b) của d

Khi đó phương trình tổng quát của d là: a(x-x₀) + b(y-y₀) = 0

* Cho đường thẳng d: ax+ by+ c= 0 nếu đường thẳng d// ∆ thì đường thẳng ∆ có dạng: ax + by + c’ = 0 (c’ ≠ c) .

B. Ví dụ minh họa

Ví dụ 1: Đường thẳng đi qua A(1; -2) , nhận n→ = (1; -2) làm véc tơ pháp tuyến có phương trình là:

A. x - 2y + 1 = 0. B. 2x + y = 0 C. x - 2y - 5 = 0 D. x - 2y + 5 = 0

Lời giải

Gọi (d) là đường thẳng đi qua A và nhận n→ = (1; -2) làm VTPT

=> Phương trình đường thẳng (d) : 1(x - 1) - 2(y + 2) = 0 hay x - 2y – 5 = 0

Chọn C.

Ví dụ 2: Viết phương trình tổng quát của đường thẳng ∆ đi qua M(1; -3) và nhận vectơ n→(1; 2) làm vectơ pháp tuyến.

A. ∆: x + 2y + 5 = 0 B. ∆: x + 2y – 5 = 0 C. ∆: 2x + y + 1 = 0 D. Đáp án khác

Lời giải

Đường thẳng ∆: qua M( 1; -3) và VTPT n→(1; 2)

Vậy phương trình tổng quát của đường thẳng ∆ là 1(x - 1) + 2(y + 3) = 0

Hay x + 2y + 5 = 0

Chọn A.

Ví dụ 3: Cho đường thẳng (d): x-2y + 1= 0 . Nếu đường thẳng (∆) đi qua M(1; -1) và song song với d thì ∆ có phương trình

A. x - 2y - 3 = 0 B. x - 2y + 5 = 0 C. x - 2y +3 = 0 D. x + 2y + 1 = 0

Lời giải

Do đường thẳng ∆// d nên đường thẳng ∆ có dạng x - 2y + c = 0 (c ≠ 1)

Ta lại có M(1; -1) ∈ (∆) ⇒ 1 - 2(-1) + c = 0 ⇔ c = -3

Vậy phương trình ∆: x - 2y - 3 = 0

Chọn A

Viết phương trình đường tròn đi qua 3 điểm

A. Phương pháp giải

Cho đường tròn ( C) đi qua ba điểm A; B và C. Lập phương trình đường tròn đi qua ba điểm :

+ Bước 1: Gọi phương trình đường tròn là ( C): x² + y² - 2ax - 2by + c = 0 (*)

( với điều kiện a² + b² - c > 0).

+Bước 2: Do điểm A; B và C thuộc đường tròn nên thay tọa độ điểm A; B và C vào (*) ta được phương trình ba phương trình ẩn a; b; c.

+ Bước 3: giải hệ phương trình ba ẩn a; b; c ta được phương trình đường tròn.

B. Ví dụ minh họa

Ví dụ 1: Tâm của đường tròn qua ba điểm A( 2; 1) ; B( 2; 5) và C( -2; 1) thuộc đường thẳng có phương trình

A. x - y + 3 = 0. B. x + y - 3 = 0 C. x - y - 3 = 0 D. x + y + 3 = 0

Hướng dẫn giải

Phương trình đường tròn (C) có dạng:

x² + y² - 2ax – 2by + c = 0 ( a² + b² – c > 0)

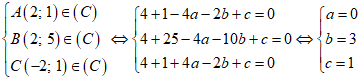
Viết phương trình đường tròn đi qua 3 điểm (đường tròn ngoại tiếp tam giác) - Toán lớp 10 ⇒ I( 0; 3)

Vậy tâm đường tròn là I( 0; 3) .

Lần lượt thay tọa độ I vào các phương trình đường thẳng thì chỉ có đường thẳng

x - y + 3 = 0 thỏa mãn.

Chọn A.

Ví dụ 2. Tìm tọa độ tâm đường tròn đi qua 3 điểm A( 0; 4); B( 2; 4) và C( 4; 0)

A. (0; 0) B. (1; 0) C. (3; 2) D. (1; 1)

Hướng dẫn giải

Phương trình đường tròn (C) có dạng:

x² + y² - 2ax – 2by + c = 0 ( a² + b² –c > 0)

Do 3 điểm A; B; C thuộc (C) nên 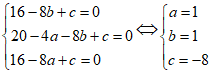Viết phương trình đường tròn đi qua 3 điểm (đường tròn ngoại tiếp tam giác) - Toán lớp 10

Vậy tâm I( 1; 1)

Chọn D.

Ví dụ 3. Tìm bán kính đường tròn đi qua 3 điểm A(0; 4); B(3; 4); C(3; 0).

A. 5 B. 3 C. √6,25 D. √8

Hướng dẫn giải

Phương trình đường tròn (C) có dạng:

x² + y² - 2ax – 2by + c = 0 ( a² + b² – c > 0)

Do 3 điểm A; B; C thuộc (C) nên 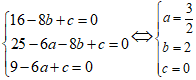Viết phương trình đường tròn đi qua 3 điểm (đường tròn ngoại tiếp tam giác) - Toán lớp 10

Vậy bán kính R = 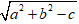Viết phương trình đường tròn đi qua 3 điểm (đường tròn ngoại tiếp tam giác) - Toán lớp 10 = √6,25.

Chọn C.

Xem thêm các dạng bài tập Toán lớp 10 chọn lọc, có đáp án hay khác:

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 10

Các dạng bài tập Phương pháp tọa độ trong mặt phẳng chọn lọc có lời giải - Toán lớp 10