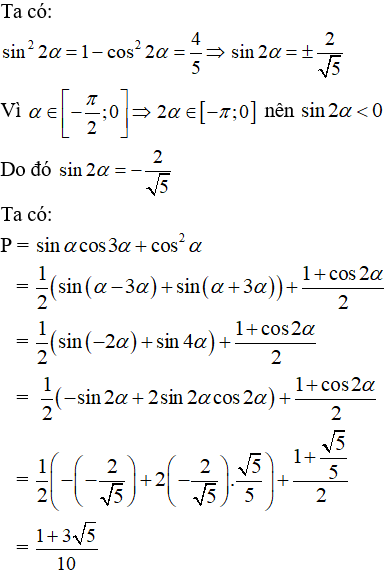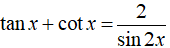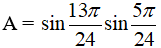Các dạng bài tập Cung và góc lượng giác, Công thức lượng giác chọn lọc có lời giải - Toán lớp 10

---

Các dạng bài tập Cung và góc lượng giác, Công thức lượng giác chọn lọc có lời giải

Với Các dạng bài tập Cung và góc lượng giác, Công thức lượng giác chọn lọc có lời giải Toán lớp 10 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Cung và góc lượng giác, Công thức lượng giác từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

Tổng hợp lý thuyết chương Cung và góc lượng giác. Công thức lượng giác

• Lý thuyết Cung và góc lượng giác Xem chi tiết
• Lý thuyết Giá trị lượng giác của một cung Xem chi tiết
• Lý thuyết Công thức lượng giác Xem chi tiết
• Lý thuyết Tổng hợp chương Cung và góc lượng giác. Công thức lượng giác Xem chi tiết

Các dạng bài tập chương Cung và góc lượng giác

• Cách đổi độ sang radian và radian sang độ cực hay, chi tiết Xem chi tiết
• Cách tính độ dài cung tròn cực hay, chi tiết Xem chi tiết
• Cách tính giá trị lượng giác của một góc, của một cung cực hay, chi tiết Xem chi tiết
• Công thức lượng giác cơ bản cực hay, chi tiết Xem chi tiết
• Giá trị lượng giác của các cung có liên quan đặc biệt cực hay, chi tiết Xem chi tiết
• Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại cực hay, chi tiết Xem chi tiết
• Cách làm bài tập Công thức cộng lượng giác cực hay, chi tiết Xem chi tiết
• Cách giải bài tập Công thức nhân đôi lượng giác cực hay, chi tiết Xem chi tiết
• Cách giải bài tập Công thức biến đổi tích thành tổng cực hay, chi tiết Xem chi tiết
• Cách giải bài tập Công thức biến đổi tổng thành tích cực hay, chi tiết Xem chi tiết

Cách làm bài tập Công thức cộng lượng giác

A. Phương pháp giải

Nhắc lại công thức cộng lượng giác:

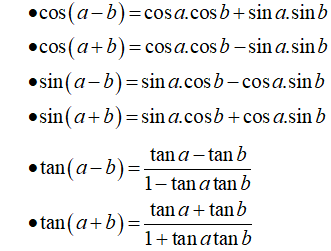
Phương pháp giải: Áp dụng các công thức biến đổi trên.

B. Ví dụ minh họa

Ví dụ 1: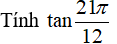

Hướng dẫn giải:

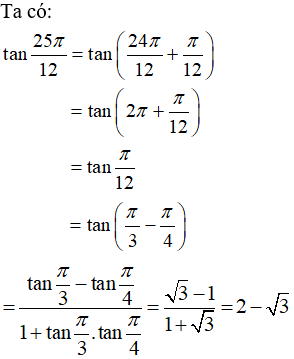
Ví dụ 2: Tính giá trị các biểu thức

a, A = cos⁡32^ocos⁡28^o - sin⁡32^osin⁡28^o

b, B = cos⁡74^ocos⁡29^o + sin⁡74^osin⁡29^o

c, C = sin⁡23^ocos⁡7^o + sin⁡7^ocos⁡23^o

d, D = sin⁡59^ocos⁡14^o - sin⁡14^ocos⁡59^o

Hướng dẫn giải:

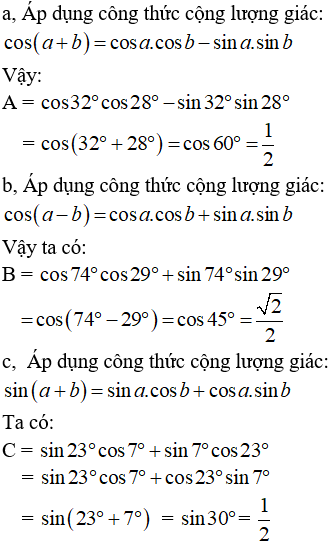
Ví dụ 3: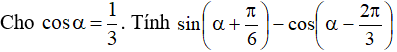

Hướng dẫn giải:

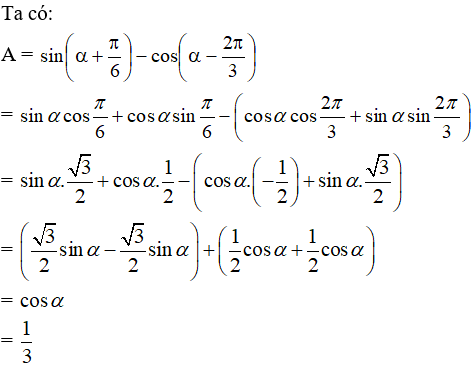
Cách giải bài tập Công thức nhân đôi lượng giác

A. Phương pháp giải

Để làm bài tập dạng này, ta cần nắm vững các công thức lượng giác đã học và công thức nhân đôi, công thức hạ bậc như sau:

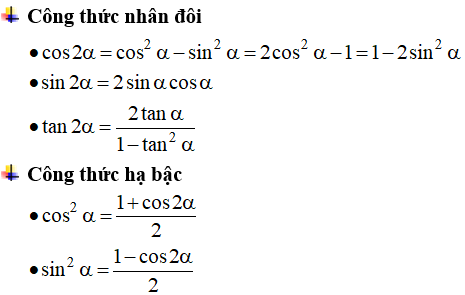
B. Ví dụ minh họa

Ví dụ 1: Tính các giá trị lượng giác của cung 2α trong các trường hợp sau:

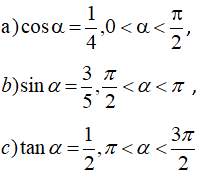
Hướng dẫn giải:

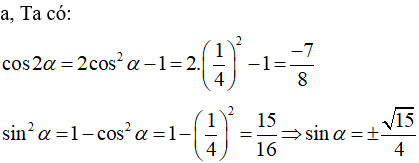
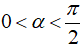
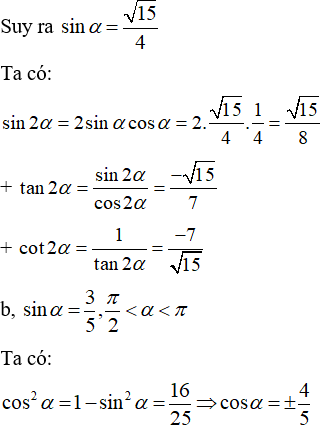
Vì nên điểm cuối của cung α thuộc góc phần tư thứ I, do đó sin⁡α > 0

Vì nên điểm cuối của cung α thuộc góc phần tư thứ II, do đó cos⁡α < 0

Vì nên điểm cuối của cung α thuộc góc phần tư thứ III, do đó cos⁡α < 0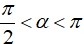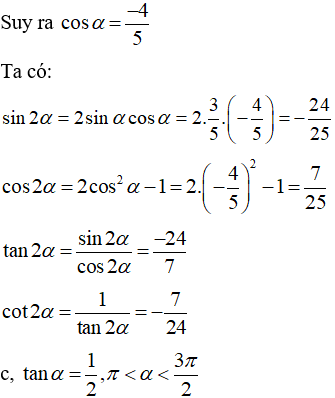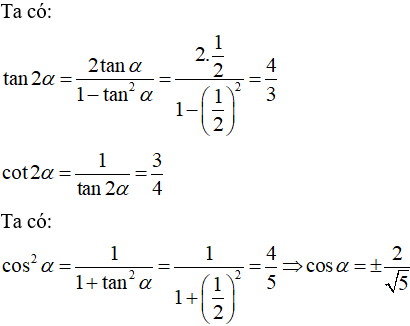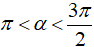

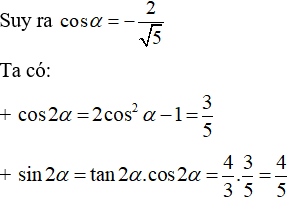
Ví dụ 2: Chứng minh đẳng thức:

Hướng dẫn giải:

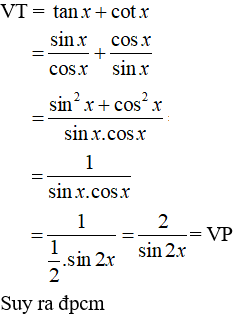
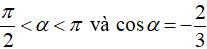
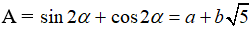
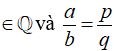
Ví dụ 3: Cho . Biết với a, b là phân số tối giản. Tính p – q.

A. 3

B. 1

C. –3

D. –1

Hướng dẫn giải:

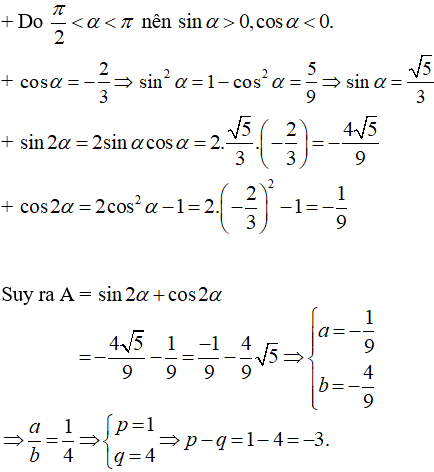
Đáp án C

Cách giải bài tập Công thức biến đổi tích thành tổng

A. Phương pháp giải

Để làm bài tập dạng này, ta phải nắm vững công thức biến đổi tích thành tổng và áp dụng để biến đổi.

Công thức biến đổi tích thành tổng:

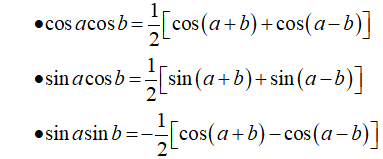
B. Ví dụ minh họa

Ví dụ 1: Tính giá trị của biểu thức

Hướng dẫn giải:

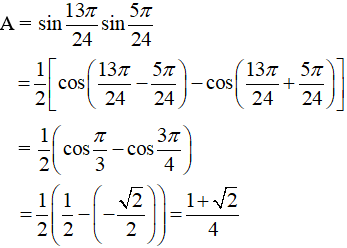
Ví dụ 2: Biến đổi thành tổng: A = 2 sin⁡x.sin⁡2x.sin⁡3x

Hướng dẫn giải:

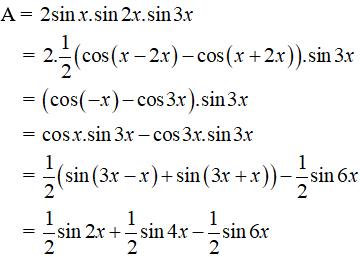
Ví dụ 3: Cho 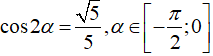. Tính P = sin⁡α.cos⁡3α + cos²⁡α

Hướng dẫn giải: