Đề thi Giữa học kì 1 Toán lớp 9 Đà Nẵng năm 2023 (7 đề)
Đề thi Giữa học kì 1 Toán lớp 9 Đà Nẵng năm 2023 (7 đề)
Haylamdo biên soạn và sưu tầm Đề thi Giữa học kì 1 Toán lớp 9 Đà Nẵng năm 2023 (7 đề) được tổng hợp chọn lọc từ đề thi môn Toán 9 của các trường trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong các bài thi Toán lớp 9.
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa Học kì 1 Đà Nẵng
Năm học 2023
Bài thi môn: Toán lớp 9
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 1)
Câu 1. (2 điểm)
a) Tìm x để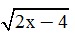 
có nghĩa.
b) Rút gọn biểu thức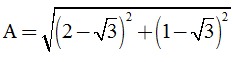 
.
Câu 2. (2 điểm)
Cho biểu thức: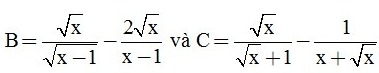 
với x > 0, x ≠ 1.
a) Rút gọn biểu thức B và C.
b) Tìm x để B.C =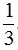 
c) Chứng minh rằng với x > 0, x ≠ 1 thì tích B.C không thể nhận giá trị nguyên.
Câu 3. (2 điểm) Giải phương trình:
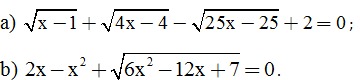
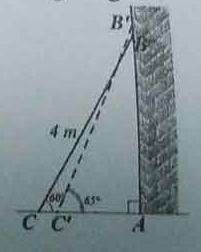
Câu 4. (1 điểm) Ở một cái thang dài 4m người ta ghi: “ Để đảm bảo an toàn khi dùng thang, phải đặt thang này tạo với mặt đất một góc có độ lớn từ 600 đến 650”. Đo góc thì khó hơn đo độ dài. Vậy hãy cho biết: Khi dùng thang đó, chân thang phải cách tường một khoảng bao nhiêu mét để đảm bảo an toàn (tham khảo hình vẽ bên)?
Câu 5. (3 điểm) Cho hình thang ABCD, ∠A = ∠D = 90o , hai đường chéo AC và BD vuông góc với nhau tại O.
a) Chứng minh rằng AD là trung bình nhân của hai đáy.
b) Cho biết AB = 18, CD = 32 . Tính OA, OB, OC, OD.
c) Chứng minh rằng các độ dài AC, BD, AB + CD là độ dài ba cạnh của một tam giác vuông.
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa Học kì 1 Đà Nẵng
Năm học 2023
Bài thi môn: Toán lớp 9
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 2)
Câu 1. (1 điểm) Tính giá trị biểu thức:
(√2019 - √2020)(√2019 + √2020).
Câu 2. (3 điểm) Giải phương trình:
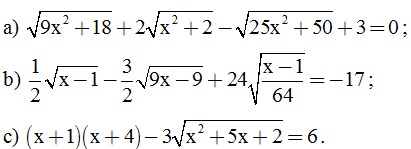
Câu 3. (2 điểm) Cho biểu thức:
.
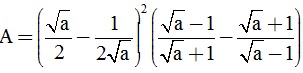a) Rút gọn A.
b) Tìm a để A < 0 .
c) Tìm a để A = -2 .
Câu 4. (3 điểm) Cho tam giác ABC vuông tại A, đường cao AH và đường phân giác AD. Cho biết DB = 51, DC = 85 .
a) Tính tỉ số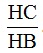 
.
b) Tính các độ dài HB, HC.
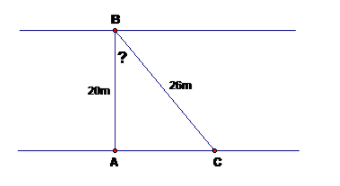
Câu 5. (1 điểm) Một khúc sông rộng 20m. Một chiếc thuyền qua sông bị dòng nước đẩy xiên nên phải chèo 26m mới sang được bờ bên kia. Hỏi dòng nước đã đẩy chiếc thuyền lệch đi một góc bao nhiêu? (góc làm tròn đến độ).
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa Học kì 1 Đà Nẵng
Năm học 2023
Bài thi môn: Toán lớp 9
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 3)
Câu 1. (2,5 điểm) Tính và rút gọn các biểu thức sau:
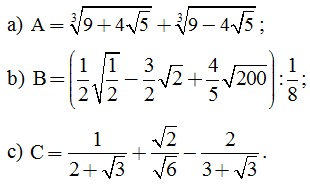
Câu 2. (2,5 điểm) Giải các phương trình sau:
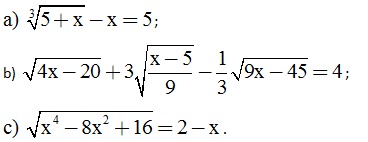
Câu 3. (2 điểm) Cho biểu thức: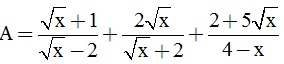 
.
a) Tìm x để biểu thức A có nghĩa.
b) Rút gọn biểu thức A.
c) Tìm x để A = 2 .
Câu 4. (1 điểm) Một cây cao 3 m. Ở một thời điểm vào ban ngày mặt trời chiếu tạo thành bóng dài 2 m. Hỏi lúc đó góc tạo bởi tia sáng mặt trời và mặt đất là bao nhiêu ? (làm tròn số đo góc tới độ).
Câu 5. (2 điểm) Cho hình thang ABCD có AB || CD và ∠C + ∠D = 90o . Biết AD = 4cm, BC = 7cm.
a) Tính số đo của góc C và góc D.
b) Cho biết thêm CD = 13cm . Tính diện tích hình thang ABCD.
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa Học kì 1 Đà Nẵng
Năm học 2023
Bài thi môn: Toán lớp 9
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 4)
Câu 1. (2 điểm)
a) Tìm điều kiện xác định của biểu thức: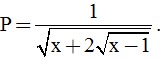 
b) So sánh: -3√5 và -5√3
Câu 2. (1,5 điểm) Thực hiện phép tính:
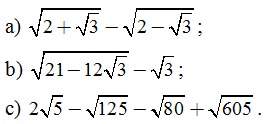
Câu 3. (2 điểm) Cho biểu thức:
.
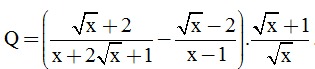a) Rút gọn Q.
b) Tìm số nguyên x để Q có giá trị nguyên.
Câu 4. (1 điểm) Tính chiều cao của một cây cổ thụ có bóng trên mặt đất dài 8m và có tia sáng từ đỉnh tạo với mặt đất một góc bằng 600.
Câu 5. (3,5 điểm) Cho ΔABC có AC = 16cm, AB = 12cm, BC = 20cm. Đường cao AH.
a) Chứng minh ΔABC vuông.
b) Tính AH, ∠B, ∠C .
c) Từ H kẻ HE, HF lần lượt vuông góc với AC, AB. Tính HE, HF.
d) So sánh: tan B và sin B (không dùng bảng và máy tính bỏ túi).
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa Học kì 1 Đà Nẵng
Năm học 2023
Bài thi môn: Toán lớp 9
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 5)
Câu 1. (2 điểm) Thực hiện phép tính:
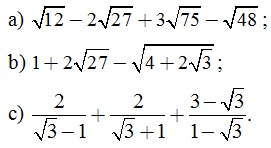
Câu 2. (2 điểm) Tìm x, biết:
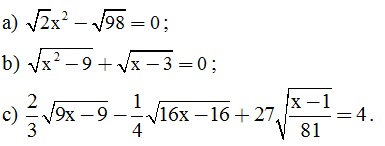
Câu 3. (2 điểm) Cho biểu thức:
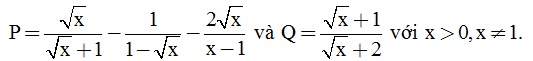
a) Tính giá trị Q tại x = 7 - 4√3 .
b) Rút gọn M = P.Q.
c) Tìm giá trị của x để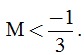 
Câu 4. (3,5 điểm)
1. Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Vẽ AH vuông góc với BC tại H.
a) Tính AH, HB, HC.
b) Gọi E, F lần lượt là hình chiếu của H trên AB, AC. Gọi O là giao điểm của AH và EF. Chứng minh 4 điểm A, E, F, H cùng thuộc một đường tròn và HB.HC = 4OE.OF.
c) Gọi M là trung điểm BC. Chứng minh SAEHF =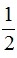 
SΔABC.
2. Một tòa nhà có chiều cao h(m). Khi tia nắng tạo với tòa nhà một góc 550 thì bóng của tòa nhà trên mặt đất dài 15m. Tính chiều cao tòa nhà.
Câu 5. (0,5 điểm) Giải phương trình: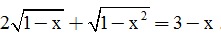
.
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa Học kì 1 Đà Nẵng
Năm học 2023
Bài thi môn: Toán lớp 9
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 6)
Bài 1. (1,5 điểm). Thực hiện phép tính.
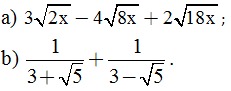
Bài 2. (2 điểm). Giải các phương trình sau:
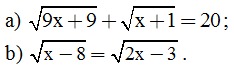
Bài 3. (2,0 điểm). Cho biểu thức:
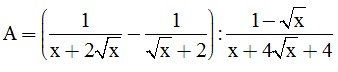
a) Tìm điều kiện xác định của A.
b) Rút gọn biểu thức A.
c) Tìm x để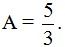 
Câu 4. (3,0 điểm) Cho ΔABC vuông tại A., đường cao AH. Biết BH = 1,8 cm; HC = 3,2 cm.
a) Tính độ dài AH ; AB; AC.
b) Tính số đo góc B và góc C.
c) Tia phân giác của góc B cắt AC tại D. Tính độ dài BD.
d) Chứng mimh rằng: tan ∠ABD =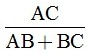 
(số đo góc làm tròn đến độ, độ dài đoạn thẳng làm tròn đến chữ số thập phân thứ ba).
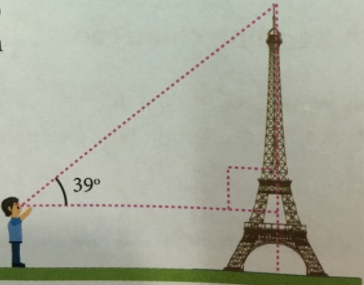
Câu 5. (1 điểm) Một người có mắt cách mặt đất 1,4m, đứng cách tháp Eiffel 400m nhìn thấy đỉnh tháp với góc nâng 39o. Tính chiều cao của tháp ( làm tròn đến mép ).
Câu 6. (0,5 điểm) Chứng minh đẳng thức sau: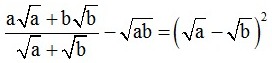 
với a > 0; b > 0
Phòng Giáo dục và Đào tạo .....
Đề thi Giữa Học kì 1 Đà Nẵng
Năm học 2023
Bài thi môn: Toán lớp 9
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 7)
Câu 1. (2 điểm) Thực hiện phép tính
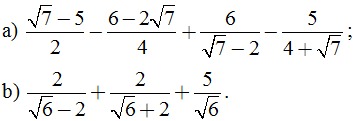
Câu 2. (2 điểm) Giải phương trình
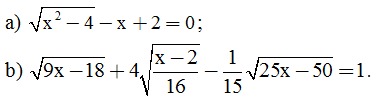
Câu 3. (2 điểm) Cho biểu thức:
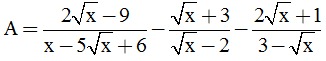
a) Tìm điều kiện xác định của A.
b) Rút gọn A.
c) Tính giá trị của A khi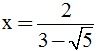 
.
d) Tìm x để A < 1.
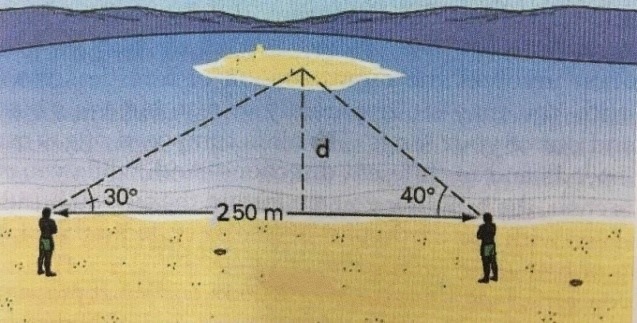
Câu 4. (1 điểm) Hai ngư dân đứng ở bên một bờ sông cách nhau 250m cùng nhìn thấy một cù lao trên sông với các góc nâng lần lượt là 30o và 40o. Tính khoảng cách d từ bờ sông đến cù lao.
Câu 5. (2,5 điểm) Cho hình thang ABCD, đáy nhỏ AB, AD ⊥ CD và AD = CD . Vẽ đường cao BH. Trên tia đối của tia DA lấy điểm K sao cho DK = CH. Gọi E là giao điểm của hai đường thẳng AD và BC. Chứng minh rằng:
a) BC ⊥ CK.
b) 
