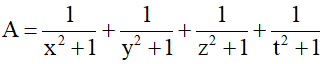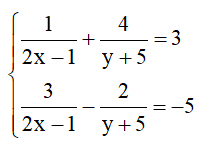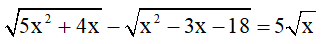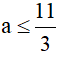Bộ đề thi Học kì 2 Toán lớp 9 năm 2023 (15 đề)
Bộ đề thi Học kì 2 Toán lớp 9 năm 2023 (15 đề)
Haylamdo biên soạn và sưu tầm Bộ đề thi Học kì 2 Toán lớp 9 năm 2023 (15 đề) được tổng hợp chọn lọc từ đề thi môn Toán 9 của các trường trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong các bài thi Toán lớp 9.
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Bài 1 (2,0 điểm) :
Cho các biểu thức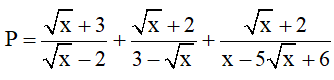 
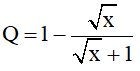
và 
với x ≥ 0, x ≠ 4, x ≠ 9
a) Tính giá trị của biểu thức Q khi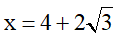 
b) Rút gọn biểu thức T = P : Q
c) Tìm x để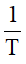 
có giá trị nguyên
Bài 2 (2,0 điểm) : Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình
Bạn An dự định thực hiện công việc quét sơn cho 40m2 tường trong một thời gian nhất định. Tuy nhiên, khi thực hiện mỗi giờ bạn An quét được ít hơn dự định là 2m2 , do đó bạn đã hoàn thành công việc chậm hơn so với kế hoạch là một giờ. Hỏi nếu đúng kế hoạch thì bạn An hoàn thành công việc trong bao lâu?
Bài 3 (2,5 điểm) :
1) Giải hệ phương trình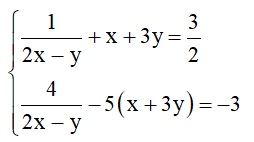 
2) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y = mx - 2m + 3 và parabol (P): y = x2
a) Tìm m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x1, x2 thỏa mãn x12x2 + x22x1 = 5 .
b) Tìm giá trị nguyên nhỏ nhất của m để (d) và (P) không có điểm chung.
Bài 4 (3,0 điểm) : Cho tam giác ABC nội tiếp đường tròn (O). Các đường cao BE và CF cắt nhau tại H.
1) Chứng minh tứ giác BFEC là tứ giác nội tiếp
2) Chứng minh
3) BE và CF lần lượt cắt (O) tại điểm thứ hai là M và N. Chứng minh EF // MN
4) Giả sử B và C cố định; A thay đổi. Tìm vị trị của A sao cho tam giác AEH có diện tích lớn nhất.
Bài 5 (0,5 điểm) : Với các số dương x, y, z, t thỏa mãn x + y + z + t = 4 Tìm giá trị nhỏ nhất của biểu thức 
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Bài 1 (2,0 điểm) : Cho hai biểu thức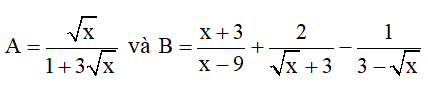 
với x ≥ 0, x ≠ 9
a) Tính giá trị của biểu thức A khi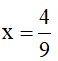 
b) Rút gọn biểu thức B
c) Cho P = A Tìm x để P < 3.
Bài 2 (2,0 điểm) : Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình
Hai công nhân cùng làm chung một công việc thì trong 8 giờ xong việc. Nếu mỗi người làm một mình, để hoàn thành công việc đó thì người thứ nhất cần nhiều hơn người thứ hai là 12 giờ. Hỏi nếu làm một mình thì mỗi người phải làm trong bao nhiêu giờ xong công việc đó?
Bài 3 (2,5 điểm) :
1) Giải hệ phương trình 
2) Cho phương trình x2 - 2(m + 1)x + 2m = 0 (1) (x là ẩn số, m là tham số)
Bài 4 (3,0 điểm) : Cho đường tròn (O) đường kính AB. Gọi H là điểm nằm giữa O và B. Kẻ dây CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E bất kỳ (E khác A và C). Kẻ CK vuông góc với AE tại K. Đường thẳng DE cắt CK tại F.
1) Chứng minh tứ giác AHCK là tứ giác nội tiếp
2) Chứng minh KH song song với ED và tam giác ACF là tam giác cân.
3) Tìm vị trí của điểm E để diện tích tam giác ADF lớn nhất.
Bài 5 (0,5 điểm) :
Giải phương trình 
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Học kì 2
Năm học 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Bài 1 (2,5 điểm) : Cho biểu thức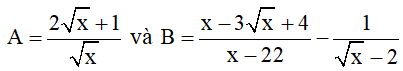 
với x > 0, x ≠ 4 .
a) Tính giá trị của A khi
b) Rút gọn biểu thức B
c) Cho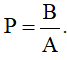 
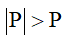
Tìm x để 
.
Bài 2 (2,0 điểm) : Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình
Một xí nghiệp theo kế hoạch phải sản xuất 75 sản phẩm trong một số ngày dự định. Trong thực tế, do cải tiến kĩ thuật nên mỗi ngày xí nghiệp làm vượt mức 5 sản phẩm, vì vậy không những họ đã làm được 80 sản phẩm mà còn hoàn thành sớm hơn kế hoạch 1 ngày. Hỏi theo kế hoạch, mỗi ngày xí nghiệp đó sản xuất bao nhiêu sản phẩm?
Bài 3 (2,5 điểm) : Cho parabol (P): y = x2 và đường thẳng (d): y = (2m + 1)x - 2m
a) Xác định tọa độ giao điểm của (d) và (P) khi m = 1
b) Tìm m để (d) và (P) cắt nhau tại hai điểm phân biệt M(x1;y1) và N(x2;y2) sao cho y1 + y2 - x1x2 = 1
Bài 4 (3,0 điểm) : Cho điểm M cố định nằm bên ngoài đường tròn (O; R). Qua M vẽ các tiếp tuyến MA, MB với đường tròn (O) (với A, B là các tiếp điểm). Gọi C là điểm bất kì trên cung nhỏ AB của đường tròn (O). Gọi D, E, F lần lượt là chân đường vuông góc kẻ từ C đến AB, MA, MB.
1) Chứng minh bốn điểm A, D, C, E cùng thuộc một đường tròn.
2) AC cắt DE tại P; BC cắt DF tại Q. Chứng minh ΔPAE ΔPDC suy ra PA.PC = PD.PE
3) Chứng minh AB // PQ
4) Khi điểm C di động trên cung nhỏ AB của đường tròn (O) thì trọng tâm G của tam giác ABC di chuyển trên đường nào?
Bài 5 (0,5 điểm) : Cho các số thực a, b, c thỏa mãn a + b + c = 7, ab + bc + ca = 15
Chứng minh rằng: 
