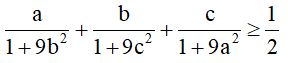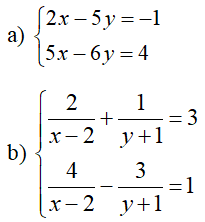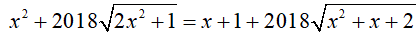Bộ đề thi Giữa kì 2 Toán lớp 9 năm 2023 (15 đề)
Bộ đề thi Giữa kì 2 Toán lớp 9 năm 2023 (15 đề)
Haylamdo biên soạn và sưu tầm Bộ đề thi Giữa kì 2 Toán lớp 9 năm 2023 (15 đề) được tổng hợp chọn lọc từ đề thi môn Toán 9 của các trường trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong các bài thi Toán lớp 9.
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa kì 2
Năm học 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Bài 1 (2,0 điểm) : Cho biểu thức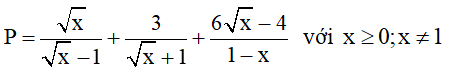 
a) Rút gọn P
b) Tìm giá trị của x để P = -1
c) So sánh P với 1
Bài 2 (2,0 điểm) : Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Một xe khách và một xe du lịch khởi hành đồng thời từ A đến B. Biết vận tốc của xe du lịch lớn hơn vận tốc của xe khách là 20km/h. Do đó nó đến B trước xe khách 50 phút. Tính vận tốc của mỗi xe, biết quãng đường AB dài 100km.
Bài 3 (2,0 điểm) : Cho hàm số y = ax2 với a ≠ 0 có đồ thị là parabol (P)
a) Xác định a biết parabol (P) đi qua điểm A(-1;1)
b) Vẽ đồ thị của hàm số y = ax2 với a vừa tìm được ở trên
c) Cho đường thẳng (d): y = 2x + 3 Tìm tọa độ giao điểm của (d) và (P) với hệ số a tìm được ở câu a.
d) Tính diện tích tam giác AOB với A và B là giao điểm của (P) và (d)
Bài 4 (3,5 điểm) : Cho đường thẳng d và đường tròn (O; R) không có điểm chung. Kẻ OH vuông góc với đường thẳng d tại H. Lấy điểm M bất kì thuộc d. Qua M kẻ hai tiếp tuyến MA, MB tới đường tròn (O; R). Nối AB cắt OH, OM lần lượt tại K và I.
a) Chứng minh 5 điểm M, H, A, O, B cùng thuộc một đường tròn
b) Chứng minh OK.OH = OI.OM
c) Chứng minh khi M di chuyển trên d thì đường thẳng AB đi qua một điểm cố định
d) Tìm vị trí của M để diện tích tam giác OIK đạt giá trị lớn nhất.
Bài 5 (0,5 điểm) : Tìm giá trị nhỏ nhất của biểu thức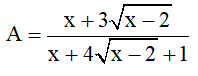 
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa kì 2
Năm học 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Bài 1 : Giải các hệ phương trình:
Bài 2 : Giải toán bằng cách lập phương trình hoặc hệ phương trình:
Theo kế hoạch hai tổ được giao sản xuât sản phẩm trong một thời gian đã định. Do cải tiến kỹ thuật nên tổ đã sản xuất vượt mức kế hoạch và tổ sản xuất vượt mức kế hoạch . Vì vậy trong cùng một thời gian quy định hai tổ đã hoàn thành vượt mức sản phẩm. Tính số sản phẩm được giao của mỗi tổ theo kế hoạch.
Bài 3 :
a) Vẽ parabol (P): y = 2x2 .
b) Viết phương trình đường thẳng (d) cắt parabol (P) tại hai điểm A và B có hoành độ lần lượt là -1 và 2 .
Bài 4 : Cho đường tròn (O;R) . Từ điểm A nằm ngoài đường tròn kẻ hai tiếp tuyến AB, AC với đường tròn ( B,C là hai tiếp điểm). Từ B kẻ đường thẳng song song với AC cắt O tại D (D khác B ), đường thẳng AD cắt O tại E ( E khác D ).
a) Chứng minh tứ giác ΔAOC nội tiếp.
b) Chứng minh: AE.AD = AB2
c) Chứng minh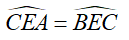 
d) Giả sử OA = 3R . Tính khoảng cách giữa hai đường thẳng AC và BD theo R .
Bài 5 : Giải phương trình:
Phòng Giáo dục và Đào tạo .....
Đề khảo sát chất lượng Giữa kì 2
Năm học 2023
Môn: Toán 9
Thời gian làm bài: 90 phút
Bài 1 (2,5 điểm) : Trong mặt phẳng tọa độ Oxy, cho Parabol (P): y = x2 và đường thẳng (d): y = -x + 2
a) Tìm tọa độ giao điểm của (P) và (Q)
b) Gọi A, B là hai giao điểm của (P) và (Q). Tính diện tích tam giác OAB.
Bài 2 (2,5 điểm) : Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Trong tháng đầu, hai tổ sản xuất được 860 chi tiết máy. Đến tháng thứ hai, tổ I vượt mức 15%, tổ II vượt mức 10%. Do đó, tháng thứ hai cả 2 tổ sản xuất được 964 chi tiết máy. Tính số chi tiết máy mỗi tổ đã sản xuất được trong tháng đầu.
Bài 3 (4,0 điểm) : Cho đường tròn tâm O đường kính AB. Dây CD vuông góc với AB tại E (E nằm giữa A và O; E không trùng A, không trùng O). Lấy điểm M thuộc cung nhỏ BC sao cho cung MB nhỏ hơn cung MC. Dây AM cắt CD tại F. Tia BM cắt đường thẳng CD tại K.
a) Chứng minh tứ giác BMFE nội tiếp
b) Chứng minh BF vuông góc với AK và
c) Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK = IF.
Bài 4 (1,0 điểm) : Với các số a, b, c > 0 và thỏa mãn a + b + c = 1
Chứng minh 
