Đề thi Học kì 1 Toán lớp 9 năm 2023 có ma trận (8 đề)
Đề thi Học kì 1 Toán lớp 9 năm 2023 có ma trận (8 đề)
Haylamdo biên soạn và sưu tầm Đề thi Học kì 1 Toán lớp 9 năm 2023 có ma trận (8 đề) được tổng hợp chọn lọc từ đề thi môn Toán 9 của các trường trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong các bài thi Toán lớp 9.
Ma trận đề thi HK1 Toán 9
|
Mức độ Chủ đề |
Nhận biết |
Thông hiểu |
Vận dụng |
Cộng |
|
Cấp độ thấp |
Cấp độ cao |
||||
|
|
|
|
||
1. Căn thức bậc hai |
Hiểu được khái niệm căn bậc 2 để giải toán tìm x |
Hiểu được hằng đẳng thức để thực hiện phép tính |
Vận dụng các phép biến đổi đơn giản để rút gọn biểu thức, tính giá trị biểu thức |
Vận dụng các phép biến đổi để rút gọn biểu thức phức tạp, giải phương trình vô tỷ |
|
|
Số câu: 2 Số điểm:1 |
Số câu: 2 Số điểm:1 |
Số câu: 2 Số điểm: 1,5. |
Số câu: 1 Số điểm:0,5 |
Số câu: 7 Số điểm: 4 |
|
2. Hàm số bậc nhất |
Nắm được các khái niệm cơ bản về hàm số như tính đồng biến nghịch biến, điểm thuộc hay không thuộc hàm số… |
Hiểu được hai đường thẳng song song, cắt nhau, giao điểm của hai đường thẳng. Vẽ được đồ thị hàm số. |
Tìm được điềm m thảo mãn điều kiện cho trước. |
||
|
Số câu:1 Số điểm: 0,5 |
Số câu: 2 Số điểm:1 |
Số câu:1 Số điểm:1 |
Số câu: 4 Số điểm: 2,5 |
||
3. Hệ thức lượng trong tam giác vuông. |
Vận dụng các hệ thức lượng trong tam giác vuông để giải toán |
||||
|
Số câu:1 Số điểm: 0,5 |
Số câu: 1 Số điểm:0,5 |
||||
4. Đường tròn |
Nhận biết được đường tròn |
Hiểu được tính chất đường tròn, hai tiếp tuyến cắt nhau để chứng minh |
Vận dụng khái niệm đường tròn và các tính chất đường tròn, hai tiếp tuyến cắt nhau của đường tròn để chứng minh |
||
|
Số câu: 1 Số điểm: 1 |
Số câu:1 Số điểm:1 |
Số câu:1 Số điểm 1 |
Số câu: 3 Số điểm: 3 |
||
Tổng |
Số câu: 4 Số điểm: 2,5 |
Số câu: 5 Số điểm: 3 |
Số câu: 5 Số điểm: 4,0 |
Số câu: 1 Số điểm: 0,5 |
Số câu: 15 Số điểm: 10 |
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 theo Thông tư 22
Năm học 2023
Bài thi môn: Toán lớp 9
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 1)
Câu 1 (1 điểm): Thực hiện phép tính
a)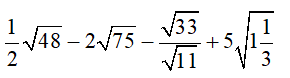 
b)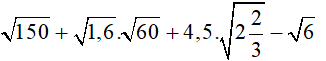 
Câu 2 (1 điểm): Tìm x
a)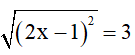 
b)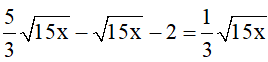 
Câu 3 (1,5 điểm): Cho biểu thức
B =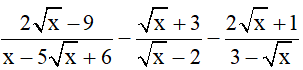 
a) Tìm điều kiện xác định và rút gọn B.
b) Tìm x nguyên để P nguyên.
Câu 4 (2,5 điểm): Cho đường thẳng d: y = mx + 1 (m ≠ 0).
a) Tìm m để hàm số đã cho đồng biến.
b) Tìm m để (d) song song với đường thẳng y = 2x + 5.
c) Biết d cắt hai trục Ox và Oy tại hai điểm A và B. Tìm m để diện tích tam giác OAB bằng 1.
Câu 5 (3,5 điểm):
1. Hai trụ điện có cùng chiều cao h được dựng thẳng đứng bên lề đối diện một đại lộ rộng 80 m. Từ một điểm M trên mặt đường nằm giữa hai trụ điện người ta nhìn thấy đỉnh hai trụ điện với góc nâng lần lượt 60' và 30'. Tính chiều cao trụ điện? (làm tròn đến chữ số thập phân thứ hai).
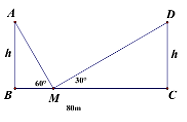
2. Cho đừng tròn (O; R) và đường thẳng d cố định không cắt đường tròn. Từ một điểm A bất kỳ trên đường thẳng d kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Từ B kẻ đường thẳng vuông góc với AO tại H, trên tia đối của tia HB lấy điểm C sao cho HC = HB.
a) Chứng minh C thuộc đường tròn (O; R) và AC là tiếp tuyến của đường tròn (O; R).
b) Từ điểm O kẻ đường thẳng vuông góc với đường thẳng d tại I, OI cắt BC tại K. Chứng minh: OH.OA = OI.OK = R2.
c) Chứng minh khi A thay đổi trên đường thẳng d thì đường thẳng BC luôn đi qua một điểm cố định.
Câu 6 (0,5 điểm): Giải phương trình: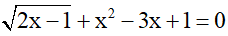 
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 theo Thông tư 22
Năm học 2023
Bài thi môn: Toán lớp 9
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 2)
Bài 1 (1 điểm): Thực hiện phép tính
a)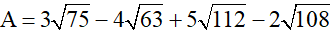 
b)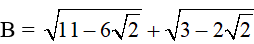 
Bài 2 (1 điểm): Tìm x
a)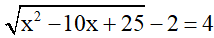 
b)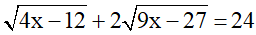 
Bài 3 (1,5 điểm): Cho biểu thức: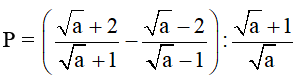
(với a > 0; a ≠ 1)
a) Rút gọn P
b) Tính giá trị của P khi a = 3 + 2√2.
Bài 4 (2,5 điểm): Cho hai đường thẳng (d): y = 3x – 1 và (d1) : y = x + 2
a) Vẽ đồ thị (d) và (d1)trên cùng một mặt phẳng tọa độ Oxy.
b) Xác định tọa độ giao điểm của hai đường thẳng (d) và (d1) bằng phương pháp tọa độ.
c) Viết phương trình đường thẳng : y = ax + b , biết song song với (d) và (d1) cắt trục hoành tại điểm có hoành độ bằng 1.
Bài 5 (3,5 điểm):
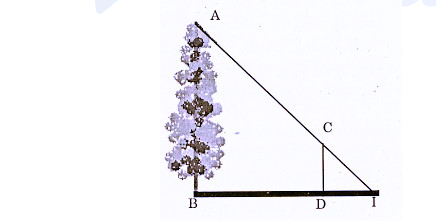
1. Để đo chiều cao của một cái cây bằng ánh nắng mặt trời, bạn An cắm một cọc CD thẳng đứng cách cây 24 mét khi bóng của cây trùng với bóng của cọc bạn An đánh dấu vị trí I. Đo khoảng cách ID được 1,6 mét. Hỏi chiều cao AB của cây? (Biết cọc có chiều cao 1,2 mét)
2. Cho đường tròn (O; 6cm), điểm A nằm bên ngoài đường tròn,
OA = 12cm. Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh BC vuông góc với OA.
b) Kẻ đường kính BD, chứng minh OA // CD.
c) Gọi K là giao điểm của AO với BC. Tính tích: OK.OA và số đo góc .
Bài 6 (0,5 điểm): Giải phương trình sau:
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 theo Thông tư 22
Năm học 2023
Bài thi môn: Toán lớp 9
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 3)
Bài 1 (1 điểm): Tìm x
a)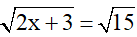 
b)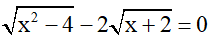 
Bài 2 (1 điểm): Thực hiện phép tính
a)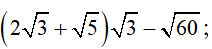
b)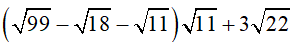 
Bài 3 (1,5 điểm): Cho biểu thức: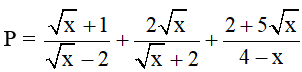 
a) Rút gọn P biết x ≥ 0, x ≠ 4.
b) Tìm x để P = 2.
Bài 4 (2,5 điểm):
a) Cho đường thẳng d1: y = (2m +1)x + 3m – 2. Tìm m để hàm số đã cho đi qua A(1; 2).
b) Vẽ đồ thị hàm số d: y = -4x + 3.
c) Cho đường thẳng d3: y = 3x + m – 1. Tìm m để khoảng cách từ O đến d bằng 2
Bài 5 (3,5 điểm):
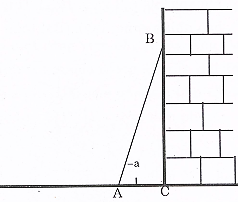
1. Một cái thang khi dựa vào tường thì góc a giữa thang và mặt đất trong khoảng từ 60o đến 65o thì an toàn. Hỏi một cái thang AB dài 3m dựng vào tường thì chân thang A cách chân tường C trong khoảng nào thì an toàn? (làm tròn 2 chữ số thập phân).
2. Từ điểm A nằm ngoài đường tròn (O; R), kẻ hai tiếp tuyến AB, AC đến đường tròn (O) (B, C là hai tiếp điểm). Gọi H là giao điểm của OA và BC.
a) Chứng minh: OA là đường trung trực của BC và OH.OA = R2.
b) Đoạn thẳng OA cắt đường tròn (O) tại M. Chứng minh: BM là tia phân giác của góc ABH.
c) Trên đoạn AH lấy điểm D sao cho HB = HD, qua D kẻ DE vuông góc với OA (E thuộc AB), gọi I là trung điểm OE. Tính số đo góc BHI và độ dài cạnh BE theo R.
Bài 6 (0,5 điểm): Giải phương trình:
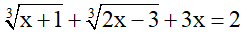
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 theo Thông tư 22
Năm học 2023
Bài thi môn: Toán lớp 9
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 4)
Bài 1 (1 điểm): Tìm x biết
a)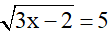 
b)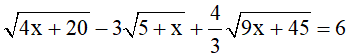 
Bài 2 (1 điểm):
a)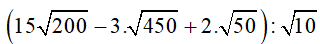
b)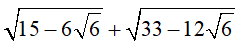
Bài 3 (1,5 điểm): Cho biểu thức: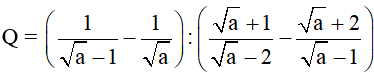 
với a > 0; a ≠ 4, a ≠ 1 .
a) Rút gọn Q
b) Tìm giá trị của a để Q dương.
Bài 4 (2,5 điểm): Cho đường thẳng (d): y = (1 – 4m)x + m – 2
a) Tìm m để (d) đi qua gốc tọa độ. Với m vừa tìm được, hãy vẽ đồ thị hàm số.
b) Chứng minh d luôn đi qua một điểm cố định, tìm điểm cố định đó.
Bài 5 (3,5 điểm):
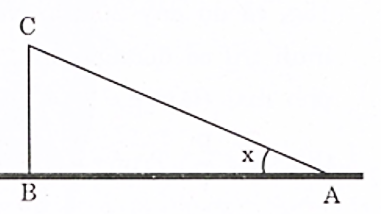
1. Một máy bay phản lực cất cánh từ vị trí A, bay lên với một góc x = 30o so với phương nằm ngang, sau một khoảng thời gian 30 giây máy bay đạt được cao độ là BC = 3000 mét. Tính vận tốc trung bình của máy bay (làm tròn đến hàng đơn vị).
2. Cho đường tròn tâm O đường kính AB. Một điểm M thuộc cung AB sao cho AM < BM. Gọi M’ là điểm đối xứng với M qua AB và S là giao điểm của hai tia BM và M’A. Gọi P là chân đường vuông góc hạ từ S xuống AB
a) Chứng minh 4 điểm A, M, S, P cùng nằm trên một đường tròn
b) Gọi S’ là giao điểm của hai tia MA và SP. Chứng minh tam giác PS’M cân
c) Chứng minh PM là tiếp tuyến của đường tròn (O)
Bài 6 (0,5 điểm): Giải phương trình:
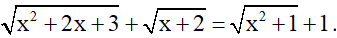
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 theo Thông tư 22
Năm học 2023
Bài thi môn: Toán lớp 9
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 5)
Bài 1 (1,5 điểm): Cho biểu thức C =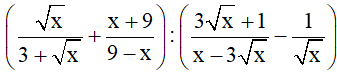 
Với x > 0 và x ≠ 9.
a) Rút gọn C;
b) Tìm x sao cho C < -1.
Bài 2 (1 điểm): Thực hiện phép tính
a) A =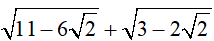 
b) B =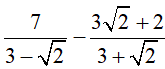 
Bài 3 (2,5 điểm): Cho đường thẳng d: y = -4x + 3
a) Vẽ đồ thị hàm số đã cho
b) Tính khoảng cách từ O đến d
c) Tính diện tích tam giác OAB với A, B là giao điểm của d với Ox, Oy
Bài 4 (1 điểm): Tìm x
a)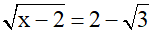 
b)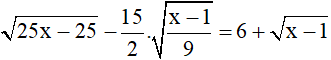 
Bài 5 (3, 5 điểm):
1. Hải đăng Trường Sa Lớn nằm trên đảo Trường Sa Lớn – “thủ phủ” quần đảo Trường Sa – có chiều cao bao nhiêu? Biết rằng tia nắng mặt trời chiếu qua đỉnh của ngọn hải đăng hợp với mặt đất 1 góc 35 độ và bóng của ngọn hải đăng trên mặt đất dài 20m.
2. Cho đường tròn (O), đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao điểm của AC và BM.
a) Chứng minh rằng NE vuông góc với AB.
b) Gọi F là điểm đối xứng với E qua M. Chứng minh rằng FA là tiếp tuyến của đường tròn (O).
c) Chứng minh FN là tiếp tuyến của đường tròn (B; BA).
Bài 6: (0,5 điểm): Giải phương trình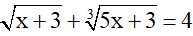 
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 theo Thông tư 22
Năm học 2023
Bài thi môn: Toán lớp 9
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 6)
Bài 1 (1 điểm): Thực hiện phép tính
a)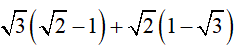 
b)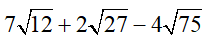 
Bài 2 (1 điểm): Tìm x
a)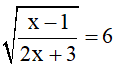 
b)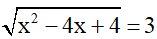 
Bài 3 (1,5 điểm): Cho biểu thức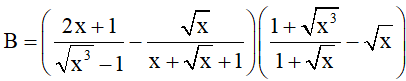 
Với x ≥ 0; x ≠ 1.
a) Rút gọn B.
b) Tìm x để B = 3.
Bài 4 (2,5 điểm): Cho đường thẳng d: y = 2x + 3m + 1.
a) Tìm m để đồ thị hàm số đi qua điểm C (0; 4)
b) Vẽ đồ thị hàm số với m vừa tìm được ở câu a.
c) Biết d cắt hai trục Ox; Oy tại hai điểm A; B. Tìm m để diện tích tam giác OAB bằng 4.
Bài 5 (3,5 điểm):
1. Tính chiều cao của một ngọn núi (làm tròn đến m) cho biết tại hai điểm A và B cách nhau 500m trên mặt đất người ta nhìn thấy đỉnh núi với góc nghiêng lần lượt là 34o và 38o (xem hình minh họa và biết ba điểm A, B, C thẳng hàng).
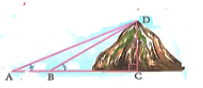
2. Cho nửa đường tròn (O) đường kính AB. M là điểm bất kỳ thuộc nửa đường tròn, H là chân đường vuông góc từ M đến AB. Vẽ đường tròn (M; MH), kẻ các tiếp tuyến AC, BD với (M) (C, D là các tiếp điểm khác H)
a) C/m: 3 điểm C, M, D thẳng hàng và CD là tiếp tuyến của (O)
b) CM: khi M di chuyển trên nửa (O) thì tổng AC + BD không đổi
c) Giả sử CD cắt AB tại I. C/m OH, OI không đổi
Bài 6 (0,5 điểm): Giải phương trình
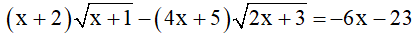
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 theo Thông tư 22
Năm học 2023
Bài thi môn: Toán lớp 9
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 7)
Bài 1 (1 điểm): Tìm x
a)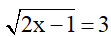 
b)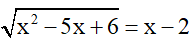 
Bài 2 (1 điểm): Thực hiện phép tính
a)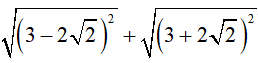 
b)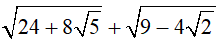 
Bài 3 (1,5 điểm): Cho biểu thức :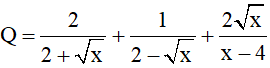 
a) Rút gọn biểu thức Q
b) Tìm x để Q = 
.
Bài 4 (2,5 điểm): Cho 2 đường thẳng: (d) và (d’)
a) Tìm m để (d) cắt (d’) tại 1 điểm C trên trục tung
b) Với m tìm được ở câu a, tìm tọa độ giao điểm A, B của (d) và (d’) với trục hoành
c) Tính diện tích và chu vi tam giác ABC
Bài 5 (3,5 điểm):
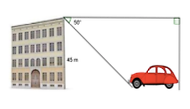
1. Từ đỉnh một tòa nhà cao 45 m, người ta nhìn thấy một ô tô đang đỗ dưới một góc nghiêng xuống là 50o. Hỏi ô tô đang đỗ cách tòa nhà đó khoảng bao nhiêu m.
2. Cho đoạn thẳng AB = 2R có O là trung điểm. Trong nửa mặt phẳng bờ AB vẽ Ax, By vuông góc với AB. Trên Ax lấy C, trên By lấy D sao cho . CMR:
a) CD = AC + BD
b) CD là tiếp tuyến của đường tròn đường kính AB
c) AC, BD không đổi khi C và D di động
Bài 6 (0,5 điểm): Giải phương trình:
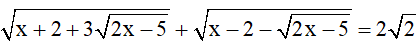
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 theo Thông tư 22
Năm học 2023
Bài thi môn: Toán lớp 9
Thời gian làm bài: phút
(không kể thời gian phát đề)
(Đề số 8)
Bài 1 (1 điểm): Tìm x biết
a)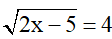 
b)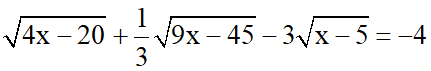 
Bài 2 (1,5 điểm): Cho biểu thức C =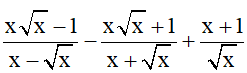 
a) Rút gọn C
b) So sánh C và 4
Bài 3 (1 điểm):
a)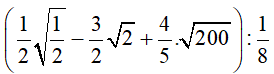 
b)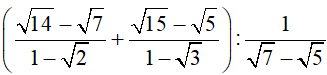 
Bài 4 (2,5 điểm): Cho hàm số y= (2-m)x + m - 1 (1). Với giá trị nào của m thì:
a) Hàm số (1) là hàm đồng biến? Nghịch biến?
b) Đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 4
c) Chứng minh rằng với mọi giá trị của m, họ đường thẳng xác định bởi hàm số (1) luôn đi qua một điểm cố định. Hãy xác định tọa độ điểm cố định đó
Bài 5 (3,5 điểm):
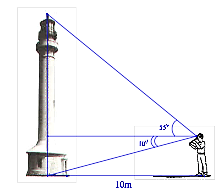
1. Một người quan sát đứng cách một cái tháp 10m, nhìn thẳng lên đỉnh tháp và chân tháp lần lượt dưới một góc 55o và 10o so với mặt đất. Hãy tính chiều cao của tháp.
2. Cho nửa đường tròn (O) đường kính AB. M là điểm bất kỳ thuộc nửa đường tròn, H là chân đường vuông góc từ M đến AB. Vẽ đường tròn (M; MH), kẻ các tiếp tuyến AC, BD với (M) (C, D là các tiếp điểm khác H)
a) C/m: 3 điểm C, M, D thẳng hàng và CD là tiếp tuyến của (O)
b) CM: khi M di chuyển trên nửa (O) thì tổng AC + BD không đổi
c) Giả sử CD cắt AB tại I. Chứng minh OH, OI không đổi
Bài 6 (0,5 điểm): Giải phương trình:
