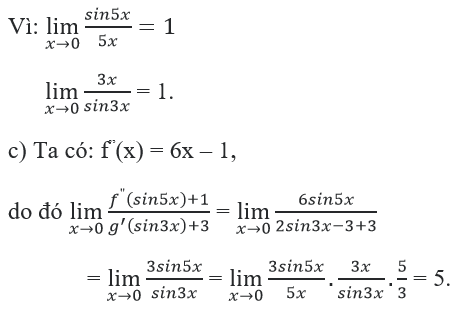Cho các hàm số f(x) = x^3 + bx^2 + cx + d, g(x) = x^2 – 3x + 1

Ôn tập cuối năm (phần Đại số và Giải tích)

Bài 20 trang 181 Toán 11: Cho các hàm số:

f(x) = x³ + bx² + cx + d (C )

g(x) = x² – 3x + 1

Với các số b, c, d tìm được ở bài 19, hãy:

a) Viết phương trình tiếp tuyến của đồ thị (C ) tại điểm có hoành độ x = –1

b) Giải phương trình f’(sinx) = 0.

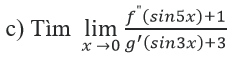
Trả lời

a) Điểm có hoành độ x = –1 thuộc đồ thị (C ) là điểm M(-1; -3). Mặt khác

f’(x) = 3x² – x, nên: f’(-1) = 3 + 1 = 4

Vậy phương trình tiếp tuyến với (C ) tại M là:

y + 3 = 4(x + 1) ⇔ y = 4x + 1.

b) Ta có f’(sin x) = 0 ⇔ 3sin²x – sin x = 0

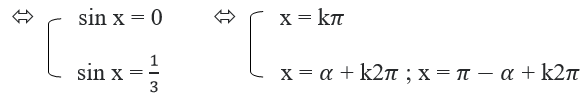
( α thỏa mãn: sin α = 1/3 và k ∈ Z ).

Vậy phương trình có 3 họ nghiệm:

x = kπ , x = α + k2π ; x = π-α + k2π ( k ∈ π , sinα = 1/3 )