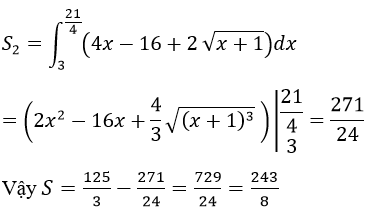Tính diện tích hình phẳng giới hạn bởi các đường. y+x^2=0 và y+3x^2=2

Câu hỏi và bài tập ôn tập cuối năm

Haylamdo biên soạn và sưu tầm lời giải Bài 15 trang 214 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 15 (trang 214 sgk Giải Tích 12 nâng cao): Tính diện tích hình phẳng giới hạn bởi các đường.

a) y+x²=0 và y+3x²=2

b) y²-4x=4 và 4x-y=16

Lời giải:

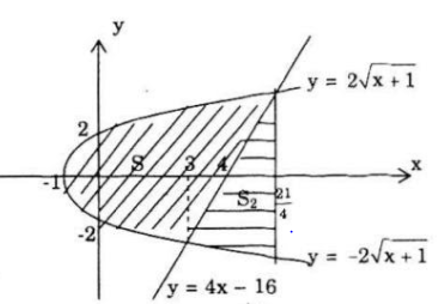
a) Hoành độ giao điểm của hai đường thẳng: y=-x² và y=-3x²+2 là nghiệm của phương trình: -x²=-3x²+2 <=> x²=1 <=> x=±1

Vậy diện tích cần tìm là:

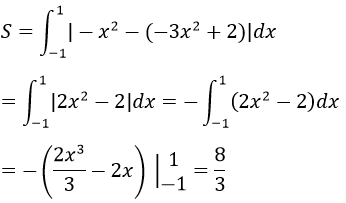
b) Ta có: y² – 4x= 4 ⇔ y² =4x+ 4 ⇔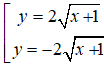

Và 4x- y = 16 ⇔ y= 4x - 16

Diện tích cần tìm là S=S₁-S₂ (hình vẽ)

Hai đường đã cho cắt nhau tại hai điểm có hoành độ là 3 và 21/4

S₁ là diện tích hình phẳn giới hạn bởi đường y²-4x-4=0 và đường thẳng x=21/4

Ta có:

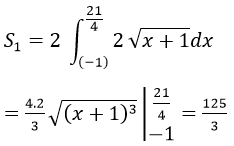
S₂ là diện tích hình phẳng giới hạn bởi 3 đường: y²=4x+4;y=4x-16 và x=21/4

Ta có: