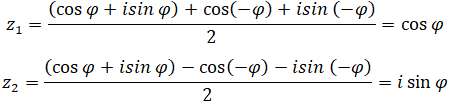Giải phương trình: z^2 -3z + 3 + i = 0

Câu hỏi và bài tập ôn tập cuối năm

Haylamdo biên soạn và sưu tầm lời giải Bài 22 trang 214 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 22 (trang 214 sgk Giải Tích 12 nâng cao):

a) Giải phương trình: z² -3z + 3 + i = 0

b) Giải phương trình: z² -(cos⁡φ+i sin⁡φ)z+i sin⁡φcos⁡φ=0

Lời giải:

a) Ta có biệt số ∆=(-3)²-4.(3+i)= -3-4i=(2i-1)² nên phương trình có hai nghiệm là z₁=i+1;z₂=2-i

b) Ta có biệt hiệu số

∆=(cos⁡φ+i sin⁡φ )²-4i sin⁡φ. cos⁡φ

=cos² φ+2i.cosφ.sinφ- sin²φ-4isinφ.cosφ=cos⁡(-2φ)+i sin⁡(-2φ)

∆ có hai căn bậc hai là: cos⁡(-φ)+i sin⁡(-φ) và (-cos⁡(-φ)-i sin⁡(-φ)

Nên phương trình có nghiệm là: