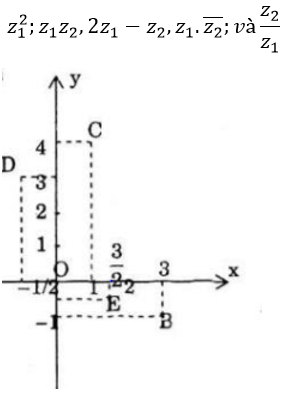
Cho các số phức z1=1+i;z2=1-2i. Hãy tính và biểu diễn hình học các số phức

Câu hỏi và bài tập ôn tập cuối năm

Haylamdo biên soạn và sưu tầm lời giải Bài 17 trang 213 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 17 (trang 213 sgk Giải Tích 12 nâng cao): Cho các số phức z₁=1+i;z₂=1-2i. Hãy tính và biểu diễn hình học các số phức: z₁²;z₁ z₂,2z₁-z₂,z₁.Z²−;và z₂/z₁ .

Lời giải:

Ta có: z₁²=(1+i)²=1+2i+i²=1+2i-1=2i

z₁ z₂=(1+i)(1-2i)=1+2+i-2i=3-i

2z₁-z₂=2(1+i)-(1-2i)=1+4i

z₁.¯(z₂ )=(1+i)(1+2i)=-1+3i

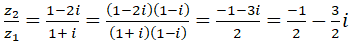
Các điểm A, B, C, D, D lần lượt biểu diễn các số: