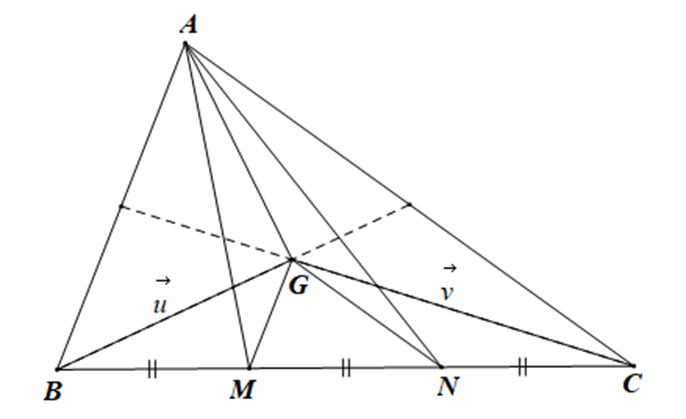
Trên cạnh BC của tam giác ABC lấy các điểm M, N không trùng với B và C

Sách bài tập Toán 10 Bài tập cuối chương 4 trang 66, 67, 68, 69, 70, 71

Bài 4.60 trang 70 sách bài tập Toán lớp 10 Tập 1: Trên cạnh BC của tam giác ABC lấy các điểm M, N không trùng với B và C sao cho BM = MN =NC.

a) Chứng minh rằng hai tam giác ABC và AMN có cùng trọng tâm.

b) Gọi G là trọng tâm của tam giác ABC. Đặt $\vec{G B} = \vec{u}$ và $\vec{G C} = \vec{v} .$ Hãy biểu thị các vectơ sau qua hai vectơ $\vec{u}$ và $\vec{v} :$ $\vec{G A}, \vec{G M}, \vec{G N} .$

Lời giải:

a) Giả sử G, G' lần lượt là trọng tâm của DABC, DAMN.

Sử dụng kết quả của Ví dụ 3, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một) ta có: $\vec{AA} + \vec{B M} + \vec{C N} = 3 \vec{G G^{'}}$

$\Rightarrow \vec{B M} + \vec{C N} = 3 \vec{G G^{'}}$

Mặt khác: M, N lần lượt lấy theo thứ tự trên cạnh BC sao cho BM = MN = NC nên ta có: $\vec{B M} = \vec{M N} = \vec{N C}$

$\Rightarrow \vec{B M} = - \vec{C N} \Rightarrow \vec{B M} + \vec{C N} = \vec{0}$

$\Rightarrow \vec{B M} + \vec{C N} = 3 \vec{G G^{'}} = \vec{0}$

Suy ra điểm G và G' trùng nhau.

Do đó hai tam giác ABC và AMN có cùng trọng tâm.

b) • Vì G là trọng tâm của tam giác ABC nên $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$

$\Rightarrow \vec{G A} = - \vec{G B} - \vec{G C}$

$\Rightarrow \vec{G A} = - \vec{u} - \vec{v}$

• Từ BM = MN = NC suy ra $\vec{M C} = - 2 \vec{M B}$

Theo Nhận xét ở Ví dụ 2, Bài 9 (trang 53, Sách bài tập, Toán 10, Tập một), với điểm G ta có:

$\vec{G C} - (- 2) \vec{G B} = (1 - (- 2)) \vec{G M}$

$\Rightarrow 3 \vec{G M} = \vec{G C} + 2 \vec{G B}$

$\Rightarrow \vec{G M} = \frac{2}{3} \vec{G B} + \frac{1}{3} \vec{G C} = \frac{2}{3} \vec{u} + \frac{1}{3} \vec{v}$

Tương tự ta cũng có: $\vec{G N} = \frac{1}{3} \vec{u} + \frac{2}{3} \vec{v}$

Xem thêm các bài giải sách bài tập Toán lớp 10 sách Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Sách bài tập Toán 10 Kết nối tri thức

Trên cạnh BC của tam giác ABC lấy các điểm M, N không trùng với B và C

Sách bài tập Toán 10 Bài tập cuối chương 4 trang 66, 67, 68, 69, 70, 71