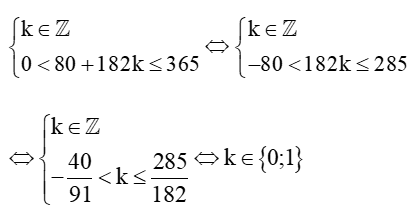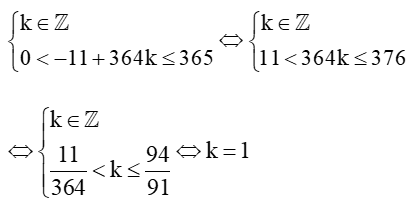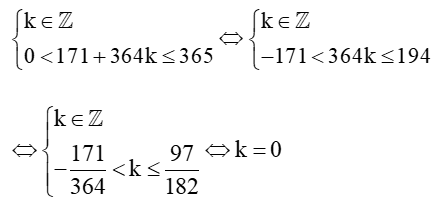Bài 4 trang 40 Toán 11 Tập 1 Cánh diều

Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ ℤ và 0 < t ≤ 365.

Giải Toán 11 Bài 4: Phương trình lượng giác cơ bản - Cánh diều

Bài 4 trang 40 Toán 11 Tập 1: Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ 40° Bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số d(t) = 3sin $(\frac{π}{182} (t - 80))$ +12 với t ∈ ℤ và 0 < t ≤ 365.

(Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2020)

a) Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm?

b) Vào ngày nào trong năm thì thành phố A có đúng 9 giờ có ánh sáng mặt trời?

c) Vào ngày nào trong năm thì thành phố A có đúng 15 giờ có ánh sáng mặt trời?

Lời giải:

a) Để thành phố A có đúng 12 giờ có ánh sáng mặt trời thì:

3sin $(\frac{π}{182} (t - 80))$ +12 = 12

$\Leftrightarrow$ sin $(\frac{π}{182} (t - 80))$ = 0

$\Leftrightarrow$ $\frac{π}{182}$ (t-80) = k $π$ (k $\in$ Z)

$\Leftrightarrow$ t - 80 = 182k (k $\in$ Z)

$\Leftrightarrow$ t = 80+182k (k $\in$ Z).

Do t ∈ ℤ và 0 < t ≤ 365 nên ta có:

Bài 4 trang 40 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Với k = 0 thì t = 80 + 182.0 = 80;

Với k = 1 thì t = 80 + 182.1 = 262.

Vậy thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày thứ 80 và ngày thứ 262 trong năm.

b) Để thành phố A có đúng 9 giờ có ánh sáng mặt trời thì:

3sin $(\frac{π}{182} (t - 80))$ +12 = 9

$\Leftrightarrow$ sin $(\frac{π}{182} (t - 80))$ = -1

$\Leftrightarrow$ $\frac{π}{182}$ (t-80) = - $\frac{π}{2}$ + k2 $π$ (k $\in$ Z)

$\Leftrightarrow$ t - 80 = -91+364k (k $\in$ Z)

$\Leftrightarrow$ t = -11+364k (k $\in$ Z)

Do t ∈ ℤ và 0 < t ≤ 365 nên ta có:

Bài 4 trang 40 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Với k = 1 thì t = ‒11 + 364.1 = 353.

Vậy thành phố A có đúng 9 giờ có ánh sáng mặt trời vào ngày thứ 353 trong năm.

c) Để thành phố A có đúng 15 giờ có ánh sáng mặt trời thì:

3sin $(\frac{π}{182} (t - 80))$ +12 = 15

$\Leftrightarrow$ sin $(\frac{π}{182} (t - 80))$ = 1

$\Leftrightarrow$ $\frac{π}{182}$ (t-80) = $\frac{π}{2}$ + k2 $π$ (k $\in$ Z)

$\Leftrightarrow$ t - 80 = 91+364k (k $\in$ Z)

$\Leftrightarrow$ t = 171+364k (k $\in$ Z)

Do t ∈ ℤ và 0 < t ≤ 365 nên ta có:

Bài 4 trang 40 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Với k = 0 thì t = 171 + 364.0 = 171.

Vậy thành phố A có đúng 15 giờ có ánh sáng mặt trời vào ngày thứ 171 trong năm.

Lời giải bài tập Toán 11 Bài 4: Phương trình lượng giác cơ bản hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Giải Toán 11 Cánh diều

Bài 4 trang 40 Toán 11 Tập 1 Cánh diều

Giải Toán 11 Bài 4: Phương trình lượng giác cơ bản - Cánh diều

Xem thêm lời giải bài tập Toán lớp 11 Cánh diều hay, chi tiết khác: