Lý thuyết Toán lớp 12 Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm - Chân trời sáng tạo

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Bài 1: Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán lớp 12 Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm - Chân trời sáng tạo

Lý thuyết Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm

1. Khoảng biến thiên

● Định nghĩa

Khoảng biến thiên, kí hiệu R, của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.

Chú ý:

- Xét mẫu số liệu ghép nhóm được cho ở bảng sau:

Nếu n₁ và n_k cùng khác 0 thì R = u_{k + 1} – u₁.

- Khoảng biến thiên của mẫu số liệu ghép nhóm luôn lớn hơn hoặc bằng khoảng biến thiên của mẫu số liệu gốc.

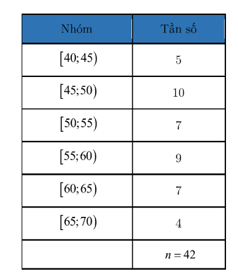
Ví dụ 1. Mẫu số liệu dưới đây ghi lại tốc độ của 42 ô tô khi đi qua một trạm đo tốc độ (đơn vị: km/h):

Hãy tìm khoảng biến thiên của mẫu số liệu ghép nhóm trên.

Hướng dẫn giải

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là

R = 70 – 40 = 30.

• Ý nghĩa của khoảng biến thiên của mẫu số liệu ghép nhóm

- Khoảng biến thiên của mẫu số liệu ghép nhóm là giá trị xấp xỉ khoảng biến thiên của mẫu số liệu gốc và có thể dùng để đo mức độ phân tán của mẫu số liệu.

- Khoảng biến thiên R = u_{k + 1} – u₁ chưa phản ánh được đầy đủ mức độ phân tán của phần lớn các số liệu. Hơn nữa, giá trị của R thường tăng vọt khi xuất hiện giá trị ngoại lệ trong mẫu số liệu. Do đó, để phản ánh mức độ phân tán của số liệu, người ta còn dùng các số đặc trưng khác.

Ví dụ 2. Thâm niên công tác của các công nhân hai nhà máy A và B được cho trong bảng sau:

Sử dụng khoảng biến thiên, hãy cho biết thâm niên công tác của công nhân nhà máy nào có độ phân tán lớn hơn.

Hướng dẫn giải

Khoảng biến thiên về thâm niên công tác của công nhân nhà máy A là:

R₁ = 25 – 0 = 25.

Khoảng biến thiên về thâm niên công tác của công nhân nhà máy B là:

R₂ = 20 – 0 = 20.

Nên theo khoảng biến thiên thì thâm niên công tác của công nhân nhà máy A phân tán hơn công nhân nhà máy B.

2. Khoảng tứ phân vị

Chú ý: Tứ phân vị thứ i, kí hiệu là Q_i với i = 1, 2, 3 của mẫu số liệu ghép nhóm (Bảng 1) được xác định như sau:

$Q_i=u_m+\frac{\frac{in}{4}-C}{n_m}\left(u_{m+1}-u_m\right)$, trong đó:

+) n = n₁ + n₂ + …+ n_k là cỡ mẫu;

+) [u_m; u_{m + 1}) là nhóm chứa tứ phân vị thứ i;

+) n_m là tần số của nhóm chứa tứ phân vị thứ i;

+) C = n₁ + n₂ + …+ n_{m – 1}.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm cũng được xác định dựa trên tứ phân vị thứ nhất và tứ phân vị thứ ba như đối với mẫu số liệu không ghép nhóm.

• Định nghĩa khoảng tứ phân vị

Xét mẫu số liệu ghép nhóm được cho ở Bảng 1.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu D_Q, là hiệu giữa tứ phân vị thứ ba Q₃ và tứ phân vị thứ nhất Q₁ của mẫu số liệu ghép nhóm đó, tức là D_Q = Q₃ – Q₁.

Ví dụ 3. Mẫu số liệu dưới đây ghi lại tốc độ của 42 ô tô khi đi qua một trạm đo tốc độ (đơn vị: km/h):

Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.

Hướng dẫn giải

Cỡ mẫu n = 42.

Gọi x₁; …; x₄₂ là tốc độ của 42 ô tô khi đi qua trạm đo tốc độ và được xếp theo thứ tự không giảm.

Tứ phân vị thứ nhất là x₁₁ mà x₁₁$\in$[45; 50) nên nhóm chứa tứ phân vị thứ nhất là [45; 50).

Có $Q_1=45+\frac{\frac{42}{4}-5}{10}.\left(50-45\right)=47,75$.

Tứ phân vị thứ ba là x₃₂ mà x₃₂$\in$[60; 65) nên nhóm chứa tứ phân vị thứ ba là [60; 65).

Có $Q_3=60+\frac{\frac{42}{4}.3-31}{7}.\left(65-60\right)\approx 60,36$.

Vậy khoảng tứ phân vị là D_Q = 60,36 – 47,75 = 12,61.

• Ý nghĩa của khoảng tứ phân vị của mẫu số liệu ghép nhóm

- Khoảng tứ phân vị của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho khoảng tứ phân vị của mẫu số liệu gốc và có thể dùng để đo mức độ phân tán của nửa giữa của mẫu số liệu (tập hợp gồm 50% số liệu nằm chính giữa mẫu số liệu).

- Khoảng tứ phân vị của mẫu số liệu ghép nhóm càng nhỏ thì dữ liệu càng tập trung xung quanh trung vị.

- Khoảng tứ phân vị được dùng để xác định giá trị ngoại lệ trong mẫu số liệu. Giá trị x trong mẫu số liệu là giá trị ngoại lệ nếu x > Q₃ + 1,5D_Q hoặc x < Q₁ – 1,5D_Q.

- Khoảng tứ phân vị của mẫu số liệu ghép nhóm không bị ảnh hưởng nhiều bởi các giá trị ngoại lệ trong mẫu số liệu.

Ví dụ 4. Người ta tiến hành phỏng vấn 40 người về một mẫu áo khoác. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm là 100. Kết quả được trình bày trong bảng ghép nhóm sau:

a) Tìm khoảng biến thiên của mẫu số liệu ghép nhóm trên.

b) Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.

c) Trong 40 người cho điểm về mẫu áo khoác đó có một người cho 50 điểm. Hỏi điểm của người này cho có phải là giá trị ngoại lệ không?

Hướng dẫn giải

a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: 100 – 50 = 50.

b) Cỡ mẫu là 40.

Giả sử x₁; x₂; …; x₄₀ là số điểm của 40 người cho mẫu áo đó, được xếp theo thứ tự không giảm.

Tứ phân vị thứ nhất là $\frac{x_{10}+x_{11}}{2}$ mà x₁₀; x₁₁ $\in$ [70; 80) nên nhóm chứa tứ phân vị thứ nhất là [70; 80).

Ta có $Q_1=70+\frac{\frac{40}{4}-9}{23}.\left(80-70\right)=\frac{1620}{23}$.

Tứ phân vị thứ ba là $\frac{x_{30}+x_{31}}{2}$ mà x₃₀; x₃₁ $\in$ [70; 80) nên nhóm chứa tứ phân vị thứ ba là [70; 80).

Ta có $Q_3=70+\frac{\frac{40.3}{4}-9}{23}.\left(80-70\right)=\frac{1820}{23}$.

Do đó ${\Delta }_Q=\frac{1820}{23}-\frac{1620}{23}=\frac{200}{23}\approx 8,7$.

c) Vì $Q_1-1,5{\Delta }_Q=\frac{1620}{23}-1,5.8,7\approx 57,38>50$ nên đây là giá trị ngoại lệ.

Bài tập Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm

Bài 1. Giá trị x được gọi là giá trị ngoại lệ nếu:

A. x < Q₃ + 1,5∆_Q.

B. x < Q₃ − 1,5∆_Q.

C. x > Q₁ − 1,5∆_Q.

D. x > Q₃ + 1,5∆_Q.

Hướng dẫn giải

Đáp án đúng là: D

Giá trị x trong mẫu số liệu là giá trị ngoại lệ nếu x > Q₃ + 1,5∆_Q hoặc x < Q₁ – 1,5∆_Q.

Bài 2. Khảo sát thời gian chạy bộ trong một ngày của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:

A. 80.

B. 60.

C. 90.

D. 100.

Hướng dẫn giải

Đáp án đúng là: D

Khoảng biến thiên của mẫu số liệu ghép nhóm là 100 – 0 = 100.

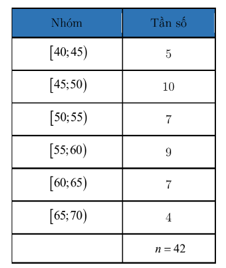
Bài 3. Chiều cao của 42 mẫu cây ở một vườn thực vật (đơn vị: centimét) được cho trong bảng sau:

Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.

Hướng dẫn giải

Cỡ mẫu n = 42.

Giả sử x₁; x₂; …; x₄₂ là chiều cao của 42 mẫu cây được xếp theo thứ tự không giảm.

Tứ phân vị thứ nhất là x₁₁ mà x₁₁ thuộc nhóm [45; 50) nên nhóm chứa tứ phân vị thứ nhất là [45; 50).

$Q_1=45+\frac{\frac{42}{4}-5}{10}.\left(50-45\right)=47,75$.

Tứ phân vị thứ ba là x₃₂ mà x₃₂ $\in$ [60; 65) nên nhóm chứa tứ phân vị thứ ba là [60; 65).

$Q_3=60+\frac{\frac{42}{4}.3-31}{7}.\left(65-60\right)\approx 60,36$.

Có ∆_Q = 60,36 – 47,75 = 12,6.

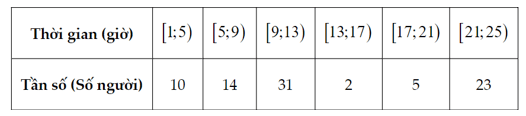
Bài 4. Một câu lạc bộ thể dục thể thao đã ghi lại số giờ các thành viên của mình sử dụng cơ sở vật chất của câu lạc bộ để tập luyện trong tháng. Kết quả thu được trong bảng sau:

Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.

Hướng dẫn giải

Cỡ mẫu n = 85.

Giả sử x₁; …; x₈₅ là thời gian sử dụng cơ sở vật chất của câu lạc bộ để tập luyện trong tháng của 85 thành viên được xếp theo thứ tự không giảm.

Tứ phân vị thứ nhất là $\frac{x_{21}+x_{22}}{2}$ mà x₂₁; x₂₂ $\in$ [5; 9) nên nhóm chứa tứ phân vị thứ nhất là [5; 9).

Ta có $Q_1=5+\frac{\frac{85}{4}-10}{14}.\left(9-5\right)=\frac{115}{14}$.

Tứ phân vị thứ ba là $\frac{x_{64}+x_{65}}{2}$ mà x₆₄; x₆₅ $\in$ [21; 25) nên nhóm chứa tứ phân vị thứ ba là [21; 25).

Ta có $Q_3=21+\frac{\frac{85}{4}.3-62}{23}.\left(25-21\right)=\frac{490}{23}$.

Do đó ${\Delta }_Q=\frac{490}{23}-\frac{115}{14}=\frac{4215}{322}\approx 13$.

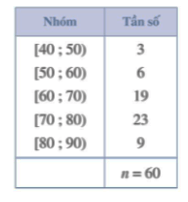
Bài 5. Số tiền (đơn vị: nghìn đồng) mua sách của 60 khách hàng ở một cửa hàng trong một ngày được thống kê lại dưới bảng sau:

a) Tìm khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.

b) Trong 60 khách hàng mua sách có 1 khách hàng trả 40 nghìn đồng. Hỏi số tiền của khách hàng này có phải là giá trị ngoại lệ không?

Hướng dẫn giải

a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 90 – 40 = 50.

Cỡ mẫu n = 60.

Giả sử x₁; x₂; …; x₆₀ là số tiền của 60 khách hàng mua sách được xếp theo thứ tự không giảm.

Tứ phân vị thứ nhất là $\frac{x_{15}+x_{16}}{2}$ mà x₁₅; x₁₆ $\in$ [60; 70) nên nhóm chứa tứ phân vị thứ nhất là [60; 70).

Ta có $Q_1=60+\frac{\frac{60}{4}-9}{19}.\left(70-60\right)=\frac{1200}{19}$.

Tứ phân vị thứ ba là $\frac{x_{45}+x_{46}}{2}$ mà x₄₅; x₄₆ $\in$ [70; 80) nên nhóm chứa tứ phân vị thứ ba là [70; 80).

Ta có $Q_3=70+\frac{\frac{60}{4}.3-28}{23}.\left(80-70\right)=\frac{1780}{23}$.

Do đó ${\Delta }_Q=\frac{1780}{23}-\frac{1200}{19}=\frac{6220}{437}\approx 14,23$.

b) Vì $Q_1-1,5{\Delta }_Q=\frac{1200}{19}-1,5.14,23\approx 41,81>40$ nên số tiền mua sách của khách này là giá trị ngoại lệ.

Học tốt Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm

Các bài học để học tốt Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài 1: Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm