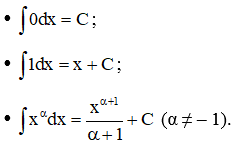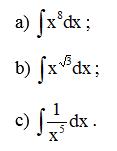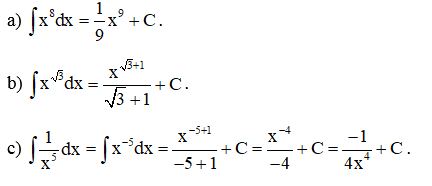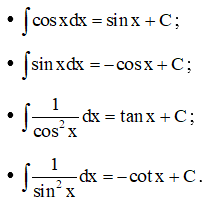Lý thuyết Toán 12 Chân trời sáng tạo Học kì 2 (hay, chi tiết)

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Học kì 1 Chân trời sáng tạo hay nhất, chi tiết bám sát nội dung từng bài học sgk Toán 12 Tập 2 sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm Toán 12.

Lý thuyết Toán 12 Học kì 2 - Chân trời sáng tạo

Lý thuyết Nguyên hàm - Chân trời sáng tạo

Lý thuyết Nguyên hàm

1. Khái niệm nguyên hàm

• Định nghĩa: Kí hiệu K là một khoảng hoặc đoạn hoặc nửa khoảng của ℝ.

Cho hàm số f(x) xác định trên K. Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x thuộc K.

Ví dụ 1. Chứng minh rằng hàm số F(x) = $\frac{x^4}{4}+x$ là một nguyên hàm của hàm số f(x) = x³ + 1 trên ℝ.

Hướng dẫn giải

Ta có F'(x) = ${\left(\frac{x^4}{4}+x\right)}^{\text{'}}=x^3+1$  = f(x) với mọi x ∈ ℝ.

Vậy hàm số F(x) = $\frac{x^4}{4}+x$  là một nguyên hàm của hàm số f(x) = x³ + 1 trên ℝ.

• Định lí: Cho F(x) là một nguyên hàm của hàm số f(x) trên K. Khi đó:

+ Với mỗi hằng số C, hàm số F(x) + C cũng là một nguyên hàm của f(x) trên K;

+ Nếu G(x) là một nguyên hàm của hàm số f(x) trên K thì tồn tại hằng số C sao cho G(x) = F(x) + C với mọi x thuộc K.

Như vậy, mọi nguyên hàm của hàm số f(x) trên K đều có dạng F(x) + C, với C là hằng số. Ta gọi F(x) + C, C ∈ ℝ là họ tất cả các nguyên hàm của f(x) trên K, kí hiệu $\int f\left(x\right)dx$  và viết

$\int f\left(x\right)dx$ = F(x) + C.

Chú ý: Biểu thức f(x)dx gọi là vi phân của nguyên hàm F(x) của f(x), kí hiệu là dF(x). Vậy dF(x) = F'(x)dx = f(x)dx.

Ví dụ 2. Tìm $\int \cos xdx$  trên ℝ.

Hướng dẫn giải

Vì (sin x)' = cos x với mọi x thuộc ℝ nên F(x) = sin x là một nguyên hàm của hàm số f(x) = cos x trên ℝ.

Vậy $\int \cos xdx$  = sin x + C trên ℝ.

Chú ý:

+ Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

Bài toán tìm nguyên hàm của một hàm số mà không chỉ rõ khoảng K thì được hiểu là tìm nguyên hàm trên từng khoảng xác định của hàm số đó.

+ Từ định nghĩa nguyên hàm, ta có: $\int f^{\text{'}}\left(x\right)dx=f\left(x\right)+C$.

2. Nguyên hàm của một số hàm số sơ cấp

2.1. Nguyên hàm của hàm số luỹ thừa

Chú ý: Người ta thường viết $\int dx$ thay cho $\int 1dx$.

Ví dụ 3. Tìm:

Hướng dẫn giải

2.2. Nguyên hàm của hàm số y = $\frac{1}{x}$

• Ta có: $\int \frac{1}{x}dx=\ln \left|x\right|+C$ .

Ví dụ 4. Cho hàm số f(x) = $\frac{1}{x}$ với x ≠ 0.

Tìm nguyên hàm F(x) của f(x) thỏa mãn F(3) = 1.

Hướng dẫn giải

Ta có $\int \frac{1}{x}dx=\ln \left|x\right|+C$ nên F(x) = ln|x| + C (x ≠ 0).

Do F(3) = 1 nên ln|3| + C = 1 hay C = 1 – ln3.

Vậy F(x) = ln|x| + 1 – ln3 (x ≠ 0). 

2.3. Nguyên hàm của một số hàm số lượng giác

Ví dụ 5. Tìm nguyên hàm F(x) của hàm số f(x) = sin x thỏa mãn F(0) + $F\left(\frac{\pi }{2}\right)$ = 0.

Hướng dẫn giải

Vì $\int \sin xdx=-\cos x+C$ nên F(x) = – cos x + C.

Do F(0) + $F\left(\frac{\pi }{2}\right)$ = 0 nên (– cos 0 + C) + (– cos $\frac{\pi }{2}$ + C) = 0, suy ra C = $\frac{1}{2}$ .

Vậy F(x) = – cos x + $\frac{1}{2}$ .

2.4. Nguyên hàm của hàm số mũ

• $\int e^{x}dx=e^x+C$;

• $\int a^{x}dx=\frac{a^x}{\ln a}+C$  (a > 0, a ≠ 1).

Ví dụ 6. Tìm:

a) $\int 4^{x}dx$;

b) $\int e^{3x}dx$ .

Hướng dẫn giải

a) $\int 4^{x}dx=\frac{{\displaystyle 4^x}}{{\displaystyle \ln 4}}+C$. 

b) $\int e^{3x}dx=\int {\left(e^3\right)}^{x}dx=\frac{{\left(e^3\right)}^x}{\ln \left(e^3\right)}+C=\frac{e^{3x}}{3}+C$ .

3. Tính chất cơ bản của nguyên hàm

• Tính chất 1. Nguyên hàm của tích một số với một hàm số

Cho f(x) là hàm số liên tục trên K, ta có:

$\int kf\left(x\right)dx=k\int f\left(x\right)dx$, với k ∈ ℝ, k ≠ 0.

Ví dụ 7. Tìm:

a) $\int \frac{4}{9x}dx$ ;

b) $\int 5\sin xdx$ .

Hướng dẫn giải

a)$\int \frac{4}{9x}dx$ $=\frac{4}{9}\int \frac{1}{x}dx=\frac{4}{9}\ln \left|x\right|+C$ .

b) $\int 5\sin xdx$ $=5\int \sin xdx=-5\cos x+C$.

• Tính chất 2. Nguyên hàm của tổng, hiệu hai hàm số

Cho f(x), g(x) là các hàm số liên tục trên K, ta có:

$\int \left[f\left(x\right)+g\left(x\right)\right]dx=\int f\left(x\right)dx+\int g\left(x\right)dx$

$\int \left[f\left(x\right)-g\left(x\right)\right]dx=\int f\left(x\right)dx-\int g\left(x\right)dx$

Ví dụ 8. Tìm $\int \left(4x^3-4x+5\right)dx$.

Hướng dẫn giải

Ta có: $\int \left(4x^3-4x+5\right)dx$$=4\int x^{3}dx-4\int xdx+5\int dx$

 = x⁴ – 2x² + 5x + C.

................................

................................

................................