Lý thuyết Toán lớp 12 Tích phân - Chân trời sáng tạo

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Bài 2: Tích phân sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán lớp 12 Tích phân - Chân trời sáng tạo

Lý thuyết Tích phân

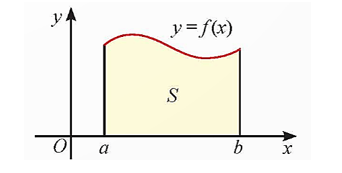
1. Diện tích hình thang cong

Cho hàm số y = f(x) liên tục và không âm trên đoạn [a; b]. Hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b được gọi là hình thang cong.

Nếu hàm số y = f(x) liên tục và không âm trên đoạn [a; b] thì diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b được tính bởi

S = F(b) – F(a),

trong đó F(x) là một nguyên hàm của f(x) trên đoạn [a; b].

Ví dụ 1. Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f(x) = 3^x, trục hoành và hai đường thẳng x = 1, x = 2.

Hướng dẫn giải

Hàm số y = 3^x liên tục, dương trên đoạn [1; 2] và có một nguyên hàm là F(x) = $\frac{3^x}{\ln 3}$.

Do đó, diện tích hình thang cong cần tìm là:

S = F(2) – F(1) = $\frac{3^2}{\ln 3}-\frac{3^1}{\ln 3}=\frac{6}{\ln 3}$.

2. Khái niệm tích phân

Cho hàm số f(x) liên tục trên đoạn [a; b]. Nếu F(x) là một nguyên hàm của f(x) trên đoạn [a; b] thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$.

Hiệu số F(b) – F(a) còn được kí hiệu là ${\left.F\left(x\right)\right|}_a^b$.

Vậy $\underset{a}{\overset{b}{\int }}f\left(x\right)dx={\left.F\left(x\right)\right|}_a^b=F\left(b\right)-F\left(a\right)$.

Ta gọi $\underset{a}{\overset{b}{\int }}$là dấu tích phân, a và b là cận tích phân, a là cận dưới, b là cận trên, f(x)dx là biểu thức dưới dấu tích phân và f(x) là hàm số dưới dấu tích phân.

Chú ý:

+ Trong trường hợp a = b hoặc a > b, ta quy ước

$\underset{a}{\overset{a}{\int }}f\left(x\right)dx=0và\underset{a}{\overset{b}{\int }}f\left(x\right)dx=-\underset{b}{\overset{a}{\int }}f\left(x\right)dx$.

+ Tích phân chỉ phụ thuộc vào hàm số f và các cận a, b mà không phụ thuộc vào biến số x hay t, nghĩa là $\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\underset{a}{\overset{b}{\int }}f\left(t\right)dt$.

+ Ý nghĩa hình học của tích phân

Nếu hàm số y = f(x) liên tục và không âm trên đoạn [a; b] thì $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ là diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b.

Vậy S = $\underset{a}{\overset{b}{\int }}f\left(x\right)dx$.

Ví dụ 2. Tính các tích phân sau:

a)$\underset{2}{\overset{3}{\int }}4xdx$;

b) $\underset{0}{\overset{1}{\int }}{e}^{x}dx$.

Hướng dẫn giải

a) $\underset{2}{\overset{3}{\int }}4xdx$$=2{\left.x^2\right|}_2^3$ = 2(3² – 2²) = 10. 

b) $\underset{0}{\overset{1}{\int }}{e}^{x}dx$$={\left.e^x\right|}_0^1$= e¹ – e⁰ = e – 1.

Chú ý:

+ Nếu hàm số f(x) có đạo hàm f'(x) và f'(x) liên tục trên đoạn [a; b] thì

f(b) – f(a) = $\underset{a}{\overset{b}{\int }}{f}^{\text{'}}\left(x\right)dx$.

+ Ta đã biết rằng, đạo hàm của quãng đường di chuyển của vật theo thời gian bằng tốc độ của chuyển động tại mỗi thời điểm (v(t) = s'(t)). Do đó, nếu biết tốc độ v(t) tại mọi thời điểm t ∈ [a; b] thì tính được quãng đường di chuyển trong khoảng thời gian từ a đến b theo công thức

s = s(b) – s(a) = $\underset{a}{\overset{b}{\int }}v\left(t\right)dt$.

Ví dụ 3. Một ô tô đang di chuyển với tốc độ 20 m/s thì hãm phanh và chuyển động chậm dần đều với tốc độ v(t) = 20 – 4t (m/s) (0 ≤ t ≤ 5). Tính quãng đường xe di chuyển từ khi hãm phanh đến khi dừng hẳn.

Hướng dẫn giải

Xe dừng hẳn khi v(t) = 20 – 4t = 0 hay t = 5 (v(t) = 20 – 4t ≥ 0 với mọi t ∈ [0; 5]).

Vậy quãng đường ô tô di chuyển từ khi bắt đầu hãm phanh đến khi dừng hẳn là:

 $s=\underset{0}{\overset{5}{\int }}v\left(t\right)dt=\underset{0}{\overset{5}{\int }}\left(20-4t\right)dt={\left.\left(20t-2t^2\right)\right|}_0^5=50$ (m).

Nhận xét: Cho hàm số f(x) liên tục trên đoạn [a; b]. Khi đó, $\frac{1}{b-a}\underset{a}{\overset{b}{\int }}f\left(x\right)dx$ được gọi là giá trị trung bình của hàm số f(x) trên đoạn [a; b].

3. Tính chất của tích phân

• Tính chất 1. Cho hàm số y = f(x) liên tục trên đoạn [a; b], k là số thực. Khi đó:

$\underset{a}{\overset{b}{\int }}kf\left(x\right)dx=k\underset{a}{\overset{b}{\int }}f\left(x\right)dx$.

Ví dụ 4. Cho $\underset{-1}{\overset{3}{\int }}f\left(x\right)dx=2$. Tính $\underset{-1}{\overset{3}{\int }}8f\left(x\right)dx$.

Hướng dẫn giải

Ta có: $\underset{-1}{\overset{3}{\int }}8f\left(x\right)dx=8\underset{-1}{\overset{3}{\int }}f\left(x\right)dx=8\cdot 2=16$.

• Tính chất 2. Cho hai hàm số y = f(x), y = g(x) liên tục trên đoạn [a; b]. Khi đó:

$\underset{a}{\overset{b}{\int }}\left[f\left(x\right)+g\left(x\right)\right]dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx+\underset{a}{\overset{b}{\int }}g\left(x\right)dx$;

$\underset{a}{\overset{b}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx=\underset{a}{\overset{b}{\int }}f\left(x\right)dx-\underset{a}{\overset{b}{\int }}g\left(x\right)dx$.

Ví dụ 5. Tính các tích phân sau:

a) $\underset{0}{\overset{2}{\int }}\left(x^2+x\right)dx$;

b) $\underset{\frac{\pi }{6}}{\overset{\frac{\pi }{4}}{\int }}\left(\frac{4}{{\sin }^{2}x}-\frac{\sqrt{3}}{{\cos }^{2}x}\right)dx$.

Hướng dẫn giải

a) $\underset{0}{\overset{2}{\int }}\left(x^2+x\right)dx=\underset{0}{\overset{2}{\int }}{x}^{2}dx+\underset{0}{\overset{2}{\int }}xdx$$={\left.\frac{x^3}{3}\right|}_0^2+{\left.\frac{x^2}{2}\right|}_0^2$

                       $=\left(\frac{8}{3}-0\right)+\left(\frac{4}{2}-0\right)=\frac{14}{3}$.

b) $\underset{\frac{\pi }{6}}{\overset{\frac{\pi }{4}}{\int }}\left(\frac{4}{{\sin }^{2}x}-\frac{\sqrt{3}}{{\cos }^{2}x}\right)dx$$=4\underset{\frac{\pi }{6}}{\overset{\frac{\pi }{4}}{\int }}\frac{1}{{\sin }^{2}x}dx-\sqrt{3}\underset{\frac{\pi }{6}}{\overset{\frac{\pi }{4}}{\int }}\frac{1}{{\cos }^{2}x}dx$

$={\left.4\cdot \left(-\cot x\right)\right|}_{\frac{\pi }{6}}^{\frac{\pi }{4}}-\sqrt{3}\cdot {\left.\tan x\right|}_{\frac{\pi }{6}}^{\frac{\pi }{4}}$

$=-4\left(\cot \frac{\pi }{4}-\cot \frac{\pi }{6}\right)-\sqrt{3}\left(\tan \frac{\pi }{4}-\tan \frac{\pi }{6}\right)$

$=-4\left(1-\sqrt{3}\right)-\sqrt{3}\left(1-\frac{1}{\sqrt{3}}\right)$

$=-3+3\sqrt{3}$.

• Tính chất 3. Cho hàm số y = f(x) liên tục trên đoạn [a; b], c ∈ (a; b). Khi đó:

$\underset{a}{\overset{b}{\int }}f\left(x\right)dx=\underset{a}{\overset{c}{\int }}f\left(x\right)dx+\underset{c}{\overset{b}{\int }}f\left(x\right)dx$.

Ví dụ 6. Tính $\underset{-2}{\overset{1}{\int }}\left|x+1\right|dx$.

Hướng dẫn giải

Ta có: $\underset{-2}{\overset{1}{\int }}\left|x+1\right|dx$$=\underset{-2}{\overset{-1}{\int }}\left|x+1\right|dx+\underset{-1}{\overset{1}{\int }}\left|x+1\right|dx$

$=\underset{-2}{\overset{-1}{\int }}\left(-x-1\right)dx+\underset{-1}{\overset{1}{\int }}\left(x+1\right)dx$

$=\left[\left(-\frac{1}{2}+1\right)-\left(-2+2\right)\right]+\left[\left(\frac{1}{2}+1\right)-\left(\frac{1}{2}-1\right)\right]$= $\frac{5}{2}$.

Bài tập Tích phân

Bài 1. Tích phân $\underset{1}{\overset{2}{\int }}\frac{2}{\sqrt{x}}dx$ có giá trị bằng:

A. $4\sqrt{2}+4$.

B. $4\sqrt{2}-1$.

C. $4\sqrt{2}-4$.

D. $4-4\sqrt{2}$.

Hướng dẫn giải

Đáp án đúng là: C

Ta có: $\underset{1}{\overset{2}{\int }}\frac{2}{\sqrt{x}}dx$$=2\underset{1}{\overset{2}{\int }}{x}^{-\frac{1}{2}}dx={\left.2\cdot \frac{x^{\frac{1}{2}}}{\frac{1}{2}}\right|}_1^2={\left.4\sqrt{x}\right|}_1^2$$=4\left(\sqrt{2}-\sqrt{1}\right)=4\sqrt{2}-4$.

Bài 2. Nếu $\underset{-1}{\overset{1}{\int }}f\left(x\right)dx=4$ và $\underset{1}{\overset{2}{\int }}f\left(x\right)dx=-5$ thì $\underset{-1}{\overset{2}{\int }}f\left(x\right)dx$ bằng:

A. 9.

B. 1.

C. – 9.

D. – 1.

Hướng dẫn giải

Đáp án đúng là: D

Ta có: $\underset{-1}{\overset{2}{\int }}f\left(x\right)dx$$=\underset{-1}{\overset{1}{\int }}f\left(x\right)dx+\underset{1}{\overset{2}{\int }}f\left(x\right)dx=4+\left(-5\right)=-1$.

Bài 3. Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số y = x⁴, trục hoành và hai đường thẳng x = $\frac{1}{2}$, x = 1.

Hướng dẫn giải

Hàm số y = x⁴ liên tục, dương trên đoạn $\left[\frac{1}{2};1\right]$ nên diện tích hình thang cong giới hạn bởi đồ thị hàm số y = x⁴, trục hoành và hai đường thẳng x = $\frac{1}{2}$, x = 1 là:

S = $\underset{\frac{1}{2}}{\overset{1}{\int }}{x}^{4}dx$ = ${\left.\frac{x^5}{5}\right|}_{\frac{1}{2}}^1=\frac{31}{160}$.

Bài 4. Tính các tích phân sau:

a) $\underset{1}{\overset{3}{\int }}\frac{4}{x^5}dx$;

b) $\underset{1}{\overset{2}{\int }}\frac{2}{3x}dx$;

c) $\underset{0}{\overset{\frac{\pi }{4}}{\int }}\left(\sin x+\frac{1}{{\cos }^{2}x}-2\right)dx$;

d) $\underset{\frac{\pi }{4}}{\overset{\frac{\pi }{2}}{\int }}\left(\frac{1}{{\sin }^{2}x}-\cos x+2\right)dx$;

e) $\underset{-1}{\overset{1}{\int }}{3}^{2x}dx$;

f) $\underset{0}{\overset{1}{\int }}{e}^{-x}dx$.

Hướng dẫn giải

a) $\underset{1}{\overset{3}{\int }}\frac{4}{x^5}dx$$=4\underset{1}{\overset{3}{\int }}{x}^{-5}dx={\left.\frac{-1}{x^4}\right|}_1^3=\frac{-1}{3^4}-\left(-1\right)=\frac{80}{81}$.

b) $\underset{1}{\overset{2}{\int }}\frac{2}{3x}dx$$=\frac{2}{3}\underset{1}{\overset{2}{\int }}\frac{1}{x}dx=\frac{2}{3}{\left.\ln \left|x\right|\right|}_1^2=\frac{2}{3}\left(\ln 2-\ln 1\right)=\frac{2}{3}\ln 2$.

c) $\underset{0}{\overset{\frac{\pi }{4}}{\int }}\left(\sin x+\frac{1}{{\cos }^{2}x}-2\right)dx$$=\underset{0}{\overset{\frac{\pi }{4}}{\int }}\sin xdx+\underset{0}{\overset{\frac{\pi }{4}}{\int }}\frac{1}{{\cos }^{2}x}dx-2\underset{0}{\overset{\frac{\pi }{4}}{\int }}dx$

$={\left.-\cos x\right|}_0^{\frac{\pi }{4}}+{\left.\tan x\right|}_0^{\frac{\pi }{4}}-{\left.2x\right|}_0^{\frac{\pi }{4}}$

$=-\left(\cos \frac{\pi }{4}-\cos 0\right)+\left(\tan \frac{\pi }{4}-\tan 0\right)-2\left(\frac{\pi }{4}-0\right)$

$=-\frac{\sqrt{2}}{2}+1+1-0-\frac{\pi }{2}=\frac{4-\sqrt{2}-\pi }{2}$.

d) $\underset{\frac{\pi }{4}}{\overset{\frac{\pi }{2}}{\int }}\left(\frac{1}{{\sin }^{2}x}-\cos x+2\right)dx$$=\underset{\frac{\pi }{4}}{\overset{\frac{\pi }{2}}{\int }}\frac{1}{{\sin }^{2}x}dx-\underset{\frac{\pi }{4}}{\overset{\frac{\pi }{2}}{\int }}\cos xdx+2\underset{\frac{\pi }{4}}{\overset{\frac{\pi }{2}}{\int }}dx$

$={\left.-\cot x\right|}_{\frac{\pi }{4}}^{\frac{\pi }{2}}-{\left.\sin x\right|}_{\frac{\pi }{4}}^{\frac{\pi }{2}}+{\left.2x\right|}_{\frac{\pi }{4}}^{\frac{\pi }{2}}$

$=-\left(\cot \frac{\pi }{2}-\cot \frac{\pi }{4}\right)-\left(\sin \frac{\pi }{2}-\sin \frac{\pi }{4}\right)+2\left(\frac{\pi }{2}-\frac{\pi }{4}\right)$

$=-0+1-1+\frac{\sqrt{2}}{2}+\frac{\pi }{2}=\frac{\pi +\sqrt{2}}{2}$..>

e) $\underset{-1}{\overset{1}{\int }}{3}^{2x}dx$$=\underset{-1}{\overset{1}{\int }}{9}^{x}dx={\left.\frac{9^x}{\ln 9}\right|}_{-1}^1=\frac{9^1-9^{-1}}{\ln 9}=\frac{80}{9\ln 9}$.

f) $\underset{0}{\overset{1}{\int }}{e}^{-x}dx$$=\underset{0}{\overset{1}{\int }}{\left(e^{-1}\right)}^{x}dx={\left.\frac{{\left(e^{-1}\right)}^x}{\ln \left(e^{-1}\right)}\right|}_0^1={\left.-e^{-x}\right|}_0^1$ = – (e^{– 1} – e⁰) = $1-\frac{1}{e}$.

Bài 5. Tại một nhà máy, gọi C(x) là tổng chi phí (tính theo triệu đồng) để sản xuất x tấn sản phẩm A trong một tháng. Khi đó, đạo hàm C'(x), gọi là chi phí cận biên, cho biết tốc độ tăng tổng chi phí theo lượng sản phẩm được sản xuất. Giả sử chi phí cận biên (tính theo triệu đồng trên tấn) của nhà máy được ước lượng bởi công thức

C'(x) = 3 – 0,02x + 0,00051x² với 0 ≤ x ≤ 150.

Biết rằng C(0) = 20 triệu đồng, gọi là chi phí cố định. Tính tổng chi phí khi nhà máy sản xuất 100 tấn sản phẩm A trong tháng.

Hướng dẫn giải

Ta có: C(100) – C(0) = $\underset{0}{\overset{100}{\int }}{C}^{\text{'}}\left(x\right)dx=\underset{0}{\overset{100}{\int }}\left(3-0,02x+0,00051x^2\right)dx$

                                $=3\underset{0}{\overset{100}{\int }}dx-0,02\underset{0}{\overset{100}{\int }}xdx+0,00051\underset{0}{\overset{100}{\int }}{x}^{2}dx$

                                $={\left.3x\right|}_0^{100}-{\left.0,01x^2\right|}_0^{100}+{\left.0,00017x^3\right|}_0^{100}$ = 370.

Suy ra C(100) = C(0) + 370 = 20 + 370 = 390 (triệu đồng).

Vậy khi nhà máy sản xuất 100 tấn sản phẩm A trong tháng thì tổng chi phí là 390 triệu đồng.

Học tốt Tích phân

Các bài học để học tốt Tích phân Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài 2: Tích phân