Lý thuyết Toán lớp 12 Khảo sát và vẽ đồ thị một số hàm số cơ bản - Chân trời sáng tạo

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Bài 3: Khảo sát và vẽ đồ thị một số hàm số cơ bản sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán lớp 12 Khảo sát và vẽ đồ thị một số hàm số cơ bản - Chân trời sáng tạo

Lý thuyết Khảo sát và vẽ đồ thị một số hàm số cơ bản

1. Sơ đồ khảo sát hàm số

Để khảo sát và vẽ đồ thị hàm số y = f(x), ta thực hiện theo các bước sau:

Bước 1. Tìm tập xác định của hàm số.

Bước 2. Xét sự biến thiên của hàm số

- Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu, cực trị (nếu có) của hàm số.

- Tìm giới hạn tại vô cực, giới hạn vô cực của hàm số và các đường tiệm cận của đồ thị hàm số (nếu có).

- Lập bảng biến thiên của hàm số.

Bước 3. Vẽ đồ thị của hàm số

- Xác định các điểm cực trị (nếu có), giao điểm của đồ thị với các trục tọa độ (nếu có và dễ tìm), …

- Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).

- Vẽ đồ thị hàm số.

Chú ý: Chỉ ra tâm đối xứng và trục đối xứng của đồ thị hàm số (nếu có).

2. Khảo sát hàm sốy = ax³ + bx² + cx + d (a ≠ 0)

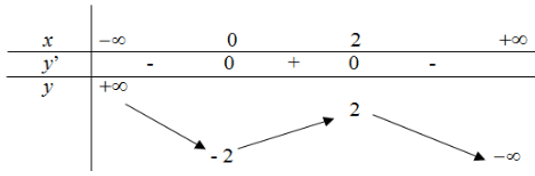
Ví dụ 1. Khảo sát và vẽ đồ thị của hàm số y = −x³ + 3x² – 2.

Hướng dẫn giải

1. Tập xác định: D = ℝ.

2. Sự biến thiên

• Chiều biến thiên

Có y' = −3x² + 6x; y' = 0 $\iff$ x = 0 hoặc x = 2.

Trên các khoảng (−∞; 0) và (2; +∞), có y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó.

Trên khoảng (0; 2), có y' > 0 nên hàm số đồng biến trên khoảng đó.

• Cực trị

Hàm số đạt cực tiểu tại x = 0 và y_CT = −2.

Hàm số đạt cực đại tại x = 2 và y_CĐ = 2.

• Các giới hạn vô cực

$\underset{x\to -\infty }{\lim }\left(-x^3+3x^2-2\right)=\underset{x\to -\infty }{\lim }{x}^3\left(-1+\frac{3}{x}-\frac{2}{x^3}\right)=+\infty$

$\underset{x\to +\infty }{\lim }\left(-x^3+3x^2-2\right)=\underset{x\to +\infty }{\lim }{x}^3\left(-1+\frac{3}{x}-\frac{2}{x^3}\right)=-\infty$

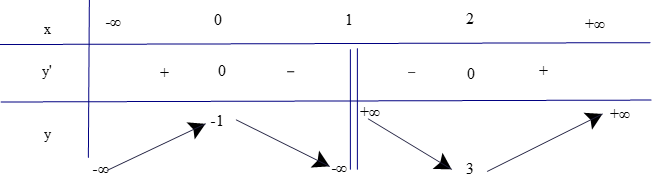
• Bảng biến thiên

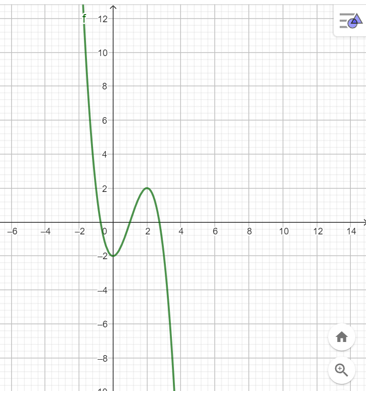
3. Đồ thị

- Đồ thị hàm số giao với trục Oy tại (0; −2).

- Có y = 0 $\iff$ −x³ + 3x² – 2 = 0 $\iff$ x = 1 hoặc $x=1-\sqrt{3}$ hoặc$x=1+\sqrt{3}$

Do đó đồ thị của hàm số giao với Ox tại 3 điểm (1; 0), $\left(1-\sqrt{3};0\right),\left(1+\sqrt{3};0\right)$

- Điểm (0; −2) là điểm cực tiểu và điểm (2; 2) là điểm cực đại của đồ thị hàm số.

- Đồ thị của hàm số có tâm đối xứng là (1; 0).

Chú ý: Đồ thị của hàm số y = ax³ + bx² + cx + d (a ≠ 0) luôn nhận điểm I(x₀; y₀) làm tâm đối xứng, trong đó x₀ là nghiệm của phương trình y" = 0 và y₀ = y(x₀).

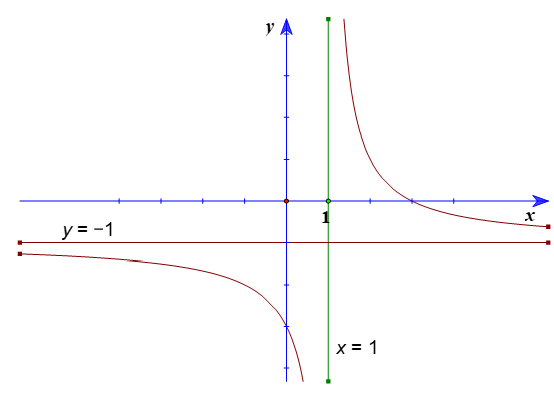
3. Khảo sát hàm số $y=\frac{ax+b}{cx+d}$ (c ≠ 0, ad – bc ≠ 0)

Ví dụ 2. Khảo sát và vẽ đồ thị của hàm số $y=\frac{1-2x}{x+1}$

Hướng dẫn giải

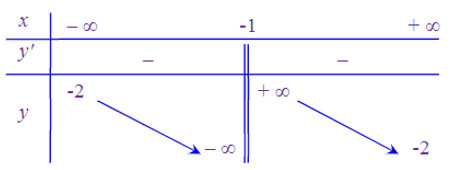
1. Tập xác định: D = ℝ\{−1}.

2. Sự biến thiên:

• Chiều biến thiên

Có $y^{\text{'}}=\frac{-3}{{\left(x+1\right)}^2}<0,\forall x\ne -1$ nên hàm số nghịch biến trên mỗi khoảng (−∞; −1) và (−1; +∞).

• Tiệm cận

Ta có $\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{1-2x}{x+1}=-2;\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{1-2x}{x+1}=-2$

Do đó y = −2 là tiệm cận ngang của đồ thị hàm số.

Ta có $\underset{x\to {\left(-1\right)}^{-}}{\lim }y=\underset{x\to {\left(-1\right)}^{-}}{\lim }\frac{1-2x}{x+1}=-\infty ;\underset{x\to {\left(-1\right)}^{+}}{\lim }y=\underset{x\to {\left(-1\right)}^{+}}{\lim }\frac{1-2x}{x+1}=+\infty$

Do đó x = −1 là tiệm cận đứng của đồ thị hàm số.

• Bảng biến thiên

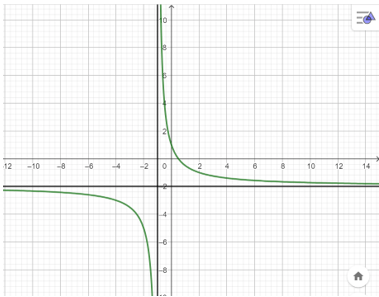
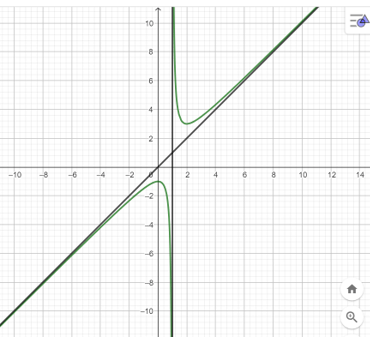
3. Đồ thị

Đồ thị của hàm số giao với trục Ox tại điểm $\left(\frac{1}{2};0\right)$, giao với trục Oy tại điểm (0; 1).

Tâm đối xứng của đồ thị hàm số là (−1; −2).

Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = −1 và y = −2.

Chú ý: Đồ thị của hàm số $y=\frac{ax+b}{cx+d}\left(c\ne 0,ad-bc\ne 0\right):$

a) Nhận giao điểm của tiệm cận đứng và tiệm cận ngang làm tâm đối xứng;

b) Nhận hai đường phân giác của các góc tạo bởi tiệm cận đứng và tiệm cận ngang làm trục đối xứng.

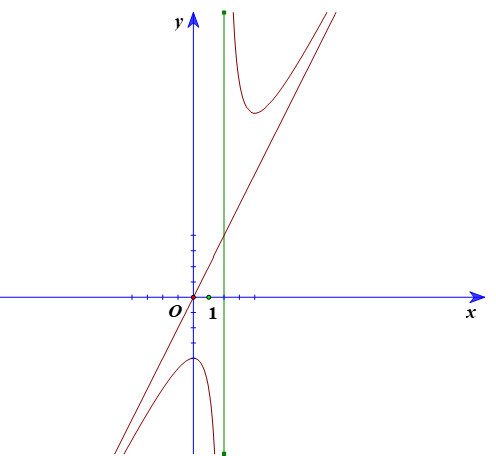
4. Khảo sát hàm số $y=\frac{a{x}^2+bx+c}{mx+n}$ (a ≠ 0, m ≠ 0, đa thức tử không chia hết cho đa thức mẫu)

Ví dụ 3. Khảo sát và vẽ đồ thị của hàm số $y=\frac{x^2-x+1}{x-1}$

Hướng dẫn giải

1. Tập xác định: D = ℝ\{1}.

2. Sự biến thiên

• Chiều biến thiên

Có $y^{\text{'}}=\frac{\left(2x-1\right)\left(x-1\right)-\left(x^2-x+1\right)}{{\left(x-1\right)}^2}=\frac{x^2-2x}{{\left(x-1\right)}^2}$

Có y' = 0 $\iff$ x² – 2x = 0 $\iff$ x = 0 hoặc x = 2.

Trên các khoảng (−∞; 0) và (2; +∞), có y' > 0 nên hàm số đồng biến trên mỗi khoảng đó.

Trên các khoảng (0; 1) và (1; 2), có y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó.

• Cực trị

Hàm số đạt cực đại tại x = 0 và y_CĐ = −1.

Hàm số đạt cực tiểu tại x = 2 và y_CT = 3.

• Các giới hạn tại vô cực và tiệm cận

$\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{x^2-x+1}{x-1}=+\infty ;\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{x^2-x+1}{x-1}=-\infty$

$\underset{x\to 1^{-}}{\lim }y=\underset{x\to 1^{-}}{\lim }\frac{x^2-x+1}{x-1}=-\infty ;\underset{x\to 1^{+}}{\lim }y=\underset{x\to 1^{+}}{\lim }\frac{x^2-x+1}{x-1}=+\infty$

Do đó x = 1 là tiệm cận đứng của đồ thị hàm số.

Ta có $a=\underset{x\to +\infty }{\lim }\frac{x^2-x+1}{x^2-x}=1$; $b=\underset{x\to +\infty }{\lim }\left(\frac{x^2-x+1}{x-1}-x\right)=\underset{x\to +\infty }{\lim }\frac{1}{x-1}=0$

Tương tự $a=\underset{x\to -\infty }{\lim }\frac{x^2-x+1}{x^2-x}=1$; $b=\underset{x\to -\infty }{\lim }\left(\frac{x^2-x+1}{x-1}-x\right)=\underset{x\to -\infty }{\lim }\frac{1}{x-1}=0$

Do đó y = x là tiệm cận xiên của đồ thị hàm số.

• Bảng biến thiên

3. Đồ thị

Đồ thị hàm số giao với trục Oy tại (0; −1).

Tâm đối xứng của đồ thị hàm số là (1; 1).

Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận là x = 1 và y = x.

Chú ý: Đồ thị của hàm số $y=\frac{a{x}^2+bx+x}{mx+n}$ ( $a\ne 0,m\ne 0$, đa thức tử không chia hết cho đa thức mẫu):

a) Nhận giao điểm của tiệm cận đứng và tiệm cận xiên làm tâm đối xứng;

b) Nhận hai đường phân giác của các góc tạo bởi tiệm cận đứng và tiệm cận xiên làm trục đối xứng.

5. Vận dụng đạo hàm và khảo sát hàm số để giải quyết một số vẫn đề liên quan đến thực tiễn

Ví dụ 4. Một khách sạn có 50 phòng. Hiện tại mỗi phòng cho thuê với giá 400 nghìn đồng một ngày thì toàn bộ phòng được thuê hết. Biết rằng cứ mỗi lần tăng giá thêm 20 nghìn đồng thì có thêm 2 phòng trống. Giám đốc muốn tìm giá cho thuê phòng để doanh thu của khách sạn trong ngày là lớn nhất.

a) Thiết lập hàm số biểu thị tổng doanh thu 1 ngày của khách sạn theo x với x là giá thuê phòng khách sạn đặt ra để có doanh thu trong ngày lớn nhất.

b) Lập bảng biến thiên của hàm số vừa tìm được.

Hướng dẫn giải

a) Gọi x là giá thuê phòng khách sạn đặt ra (nghìn đồng), x > 400.

Giá chênh lệch sau khi tăng là x – 400 nghìn đồng.

Số phòng khách sạn cho thuê giảm nếu giá x là: $\frac{\left(x-400\right).2}{20}=\frac{x-400}{10}$ (phòng).

Khi đó số phòng cho thuê với giá x là: $50-\frac{x-400}{10}=\frac{900-x}{10}$

Khi đó tổng doanh thu của khách sạn trong 1 ngày là: $f\left(x\right)=x.\left(\frac{900-x}{10}\right)=-\frac{x^2}{10}+90x$

b) Xét hàm số $y=f\left(x\right)=-\frac{x^2}{10}+90x$

Tập xác định: D = (400; +∞).

Có $y^{\text{'}}=-\frac{x}{5}+90$; $y^{\text{'}}=0\iff x=450$

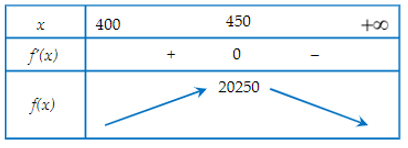
Trên khoảng (400; 450), có y' > 0 nên hàm số đồng biến trên khoảng đó.

Trên khoảng (450; +∞), có y' < 0 nên hàm số nghịch biến trên khoảng đó.

Bảng biến thiên

Bài tập Khảo sát và vẽ đồ thị một số hàm số cơ bản

Bài 1. Hàm số nào dưới đây có bảng biến thiên như sau:

A. $y=\frac{x-7}{x-5}$

B. $y=\frac{x-5}{x-1}$

C. $y=\frac{5x}{x-1}$

D. $y=\frac{x-3}{x-5}$

Hướng dẫn giải

Đáp án đúng là: D

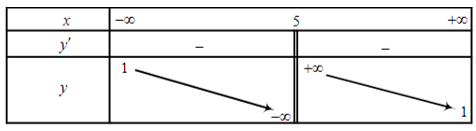
Dựa vào bảng biến thiên ta thấy:

+) x = 5 là tiệm cận đứng và y = 1 là tiệm cận ngang của đồ thị hàm số. Do đó loại B và C.

+) Hàm số nghịch biến trên (−∞; 5) và (5; +∞).

Xét đáp án A. Có $y^{\text{'}}=\frac{2}{{\left(x-5\right)}^2}>0,\forall x\ne 5$ nên loại đáp án A.

Xét đáp án D. Có $y^{\text{'}}=\frac{-2}{{\left(x-5\right)}^2}<0,\forall x\ne 5$. Do đó chọn đáp án D.

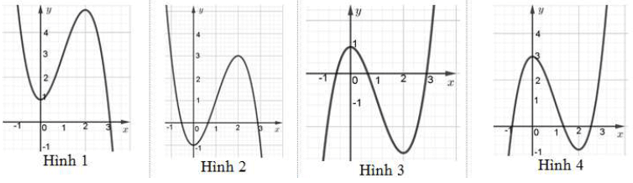
Bài 2. Đồ thị của hàm số y = −x³ + 3x² – 1 là hình nào dưới đây

A. Hình 1.

B. Hình 2.

C. Hình 3.

D. Hình 4.

Hướng dẫn giải

Đáp án đúng là: B

Vì đồ thị hàm số y = −x³ + 3x² – 1 cắt trục tung tại (0; −1). Do đó chọn B.

Bài 3. Khảo sát và vẽ đồ thị của hàm số

a) y = −x³ – x;

b) $y=\frac{-x+3}{x-1}$

Hướng dẫn giải

a) y = −x³ – x

1. Tập xác định: D = ℝ.

2. Sự biến thiên

• Chiều biến thiên

Có y’ = −3x² – 1 < 0, ∀x ∈ ℝ.

Do đó hàm số luôn nghịch biến.

Hàm số đã cho không có cực trị.

• Các giới hạn tại vô cực

$\underset{x\to +\infty }{\lim }\left(-x^3-x\right)=\underset{x\to +\infty }{\lim }{x}^3\left(-1-\frac{1}{x^2}\right)=-\infty$; $\underset{x\to -\infty }{\lim }\left(-x^3-x\right)=\underset{x\to -\infty }{\lim }{x}^3\left(-1-\frac{1}{x^2}\right)=+\infty$

• Bảng biến thiên

3. Đồ thị

Đồ thị hàm số đi qua gốc tọa độ và điểm (1; −2).

Đồ thị hàm số nhận (0; 0) làm tâm đối xứng.

b) $y=\frac{-x+3}{x-1}$

1. Tập xác định: D = ℝ\{1}.

2. Sự biến thiên

• Chiều biến thiên

Có $y^{\text{'}}=-\frac{2}{{\left(x-1\right)}^2}<0,\forall x\ne 1$

Hàm số nghịch biến trên các khoảng (−∞; 1) và (1; +∞).

Hàm số không có cực trị

• Tiệm cận

Có $\underset{x\to 1^{-}}{\lim }y=\underset{x\to 1^{-}}{\lim }\frac{-x+3}{x-1}=-\infty ;\underset{x\to 1^{+}}{\lim }y=\underset{x\to 1^{+}}{\lim }\frac{-x+3}{x-1}=+\infty$

Do đó x = 1 là tiệm cận đứng của đồ thị hàm số.

Có $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{-x+3}{x-1}=-1$; $\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{-x+3}{x-1}=-1$

Do đó y = −1 là tiệm cận ngang của đồ thị hàm số.

• Bảng biến thiên

3. Đồ thị

Đồ thị hàm số giao với Ox tại (3; 0) và giao với Oy tại (0; −3).

Tâm đối xứng của đồ thị là (1; −1).

Các trục đối xứng của đồ thị là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = 1 và y = −1.

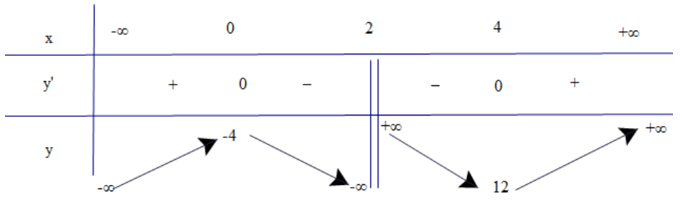
Bài 4. Khảo sát và vẽ đồ thị của hàm số $y=\frac{2x^2-4x+8}{x-2}$

Hướng dẫn giải

1. Tập xác định: D = ℝ\{2}.

2. Sự biến thiên

• Chiều biến thiên

Có $y^{\text{'}}=\frac{\left(4x-4\right)\left(x-2\right)-\left(2x^2-4x+8\right)}{{\left(x-2\right)}^2}=\frac{2x^2-8x}{{\left(x-2\right)}^2}$

y' = 0 $\iff$ 2x² – 8x = 0 $\iff$ x = 0 hoặc x = 4.

Trên các khoảng (−∞; 0) và (4; +∞), có y' > 0 nên hàm số đồng biến trên mỗi khoảng đó.

Trên các khoảng (0; 2) và (2; 4), có y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó.

• Cực trị

Hàm số đạt cực đại tại x = 0 và y_CĐ = −4.

Hàm số đạt cực tiểu tại x = 4 và y_CT = 12.

$\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{2x^2-4x+8}{x-2}=+\infty ;$ $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{2x^2-4x+8}{x-2}=-\infty$

Có $\underset{x\to 2^{-}}{\lim }y=\underset{x\to 2^{-}}{\lim }\frac{2x^2-4x+8}{x-2}=-\infty ;\underset{x\to 2^{+}}{\lim }y=\underset{x\to 2^{+}}{\lim }\frac{2x^2-4x+8}{x-2}=+\infty$

Do đó x = 2 là tiệm cận đứng của đồ thị hàm số.

Có $a=\underset{x\to +\infty }{\lim }\frac{2x^2-4x+8}{x^2-2x}=2;$ $b=\underset{x\to +\infty }{\lim }\left(\frac{2x^2-4x+8}{x-2}-2x\right)=\underset{x\to +\infty }{\lim }\frac{8}{x-2}=0$

Tương tự $a=\underset{x\to -\infty }{\lim }\frac{2x^2-4x+8}{x^2-2x}=2;$ $b=\underset{x\to -\infty }{\lim }\left(\frac{2x^2-4x+8}{x-2}-2x\right)=\underset{x\to -\infty }{\lim }\frac{8}{x-2}=0$

Do đó y = 2x là tiệm cận xiên của đồ thị hàm số.

• Bảng biến thiên

3. Đồ thị

Đồ thị hàm số giao với Oy tại (0; −4).

Tâm đối xứng của đồ thị hàm số là (2; 4).

Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = 2 và y = 2x.

Bài 5.Một tên lửa bay vào không trung với quãng đường đi được s(t) (km) là hàm phụ thuộc theo biến t (giây) theo quy tắc sau: $s\left(t\right)=e^{t^2+3}+2t{e}^{3t+1}$ (km). Hỏi vận tốc của tên lửa sau 1 giây là bao nhiêu (biết hàm biểu thị vận tốc là đạo hàm của hàm biểu thị quãng đường theo thời gian).

Hướng dẫn giải

Ta có $v\left(t\right)=s^{\text{'}}\left(t\right)=2t{e}^{t^2+3}+2e^{3t+1}+6t{e}^{3t+1}$

Vận tốc của tên lửa sau 1 giây là: $v\left(1\right)=2e^{1^2+3}+2e^{3.1+1}+6e^{3.1+1}=10e^4$ (km/s).

Học tốt Khảo sát và vẽ đồ thị một số hàm số cơ bản

Các bài học để học tốt Khảo sát và vẽ đồ thị một số hàm số cơ bản Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài 3: Khảo sát và vẽ đồ thị một số hàm số cơ bản