Lý thuyết Toán lớp 12 Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm - Chân trời sáng tạo

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Bài 2: Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán lớp 12 Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm - Chân trời sáng tạo

Lý thuyết Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm

1. Phương sai, độ lệch chuẩn

● Định nghĩa

Phương sai của mẫu số liệu ghép nhóm, kí hiệu S², được tính bởi công thức $S^2=\frac{1}{n}\left[n_1{\left(c_1-\overline{x}\right)}^2+n_2{\left(c_2-\overline{x}\right)}^2+\mathrm{...}+n_k{\left(c_k-\overline{x}\right)}^2\right]$,

trong đó: n = n₁ + n₂ + …+ n_k là cỡ mẫu; $\overline{x}=\frac{1}{n}\left(n_1{c}_1+n_2{c}_2+\mathrm{...}+n_k{c}_k\right)$ là số trung bình.

Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu S, là căn bậc hai số học của phương sai, nghĩa là $S=\sqrt{S^2}$.

Chú ý:

a) Phương sai của mẫu số liệu ghép nhóm có thể được tính theo công thức sau: $S^2=\frac{1}{n}\left(n_1{c}_1^2+n_2{c}_2^2+\mathrm{...}+n_k{c}_k^2\right)-{\overline{x}}^2$.

b) Trong thống kê, người ta còn dùng đại lượng sau để đo mức độ phân tán của mẫu số liệu ghép nhóm${\widehat{s}}^2=\frac{1}{n-1}\left[n_1{\left(c_1-\overline{x}\right)}^2+n_2{\left(c_2-\overline{x}\right)}^2+\mathrm{...}+n_k{\left(c_k-\overline{x}\right)}^2\right]$.

Ví dụ 1. Mức lương hàng tháng ở 1 công ty được Công đoàn thu thập theo bảng sau (đơn vị triệu đồng):

Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên. (làm tròn kết quả đến hàng phần mười)

Hướng dẫn giải

Ta có bảng thống kê thu nhập theo giá trị đại diện là

Cỡ mẫu n = 17 + 38 + 27 + 21 + 7 = 110.

Giá trị trung bình là $\overline{x}=\frac{17.7,5+38.12,5+27.17,5+21.22,5+7.27,5}{110}\approx 14,4$.

Phương sai:

$S^2=\frac{17.7,5^2+38.12,5^2+27.17,5^2+21.22,5^2+7.27,5^2}{110}-14,4^2\approx 75,3$.

Độ lệch chuẩn là:

$S=\sqrt{75,3}\approx 8,7$.

2. Ý nghĩa của phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm

- Phương sai (độ lệch chuẩn) của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho phương sai (độ lệch chuẩn) của mẫu số liệu gốc. Chúng được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu. Phương sai và độ lệch chuẩn càng lớn thì dữ liệu càng phân tán.

- Độ lệch chuẩn có cùng đơn vị với đơn vị của mẫu số liệu.

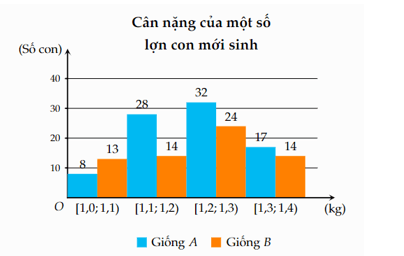
Ví dụ 2. Cân nặng của một số lợn con mới sinh thuộc hai giống A và B được cho ở biểu đồ dưới đây (đơn vị: kg)

a) Hãy tính giá trị trung bình và độ lệch chuẩn của mẫu số liệu trên.

b) Nếu so sánh theo độ lệch chuẩn thì giống nào có cân nặng đồng đều hơn?

Hướng dẫn giải

a) Từ biểu đồ ta có bảng thống kê sau:

Cân nặng	[1,0; 1,1)	[1,1; 1,2)	[1,2; 1,3)	[1,3; 1,4)
Giá trị đại diện	1,05	1,15	1,25	1,35
Giống A	8	28	32	17
Giống B	13	14	24	14

Giá trị trung bình của giống A là:

$\overline{x_A}=\frac{8.1,05+28.1,15+32.1,25+17.1,35}{85}\approx 1,22$.

Phương sai của giống A

$S_A^2=\frac{8.1,{05}^2+28.1,{15}^2+32.1,{25}^2+17.1,{35}^2}{85}-1,{22}^2\approx 0,004$.

Độ lệch chuẩn của giống A

$S_A=\sqrt{0,004}\approx 0,06$.

Giá trị trung bình của giống B là:

$\overline{x_B}=\frac{13.1,05+14.1,15+24.1,25+14.1,35}{65}=1,21$.

Phương sai của giống B

$S_B^2=\frac{13.1,{05}^2+14.1,{15}^2+24.1,{25}^2+14.1,{35}^2}{65}-1,{21}^2\approx 0,011$.

Độ lệch chuẩn của giống B là

$S_B=\sqrt{0,011}\approx 0,105$.

b) Do S_B > S_A nên giống A có cân nặng đồng đều hơn.

Bài tập Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm

Bài 1. Yếu tố được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu là:

A. Khoảng biến thiên.

B. Khoảng tứ phân vị.

C. Phương sai.

D. Phương sai và độ lệch chuẩn.

Hướng dẫn giải

Đáp án đúng là: D

Phương sai và độ lệch chuẩn dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu.

Bài 2. Chọn phương sán sai:

A. Phương sai của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho phương sai của mẫu số liệu gốc.

B. Phương sai và độ lệch chuẩn càng lớn thì dữ liệu càng phân tán.

C. Độ lệch chuẩn có cùng đơn vị với đơn vị của mẫu số liệu.

D. Phương sai có cùng đơn vị với đơn vị của mẫu số liệu.

Hướng dẫn giải

Đáp án đúng là: D

Đáp án sai là: Phương sai có cùng đơn vị với đơn vị của mẫu số liệu.

Bài 3. Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):

Doanh thu	[5; 7)	[7; 9)	[9; 11)	[11; 13)	[13; 15)
Số ngày	2	7	7	3	1

Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.

Hướng dẫn giải

Bảng thống kê có giá trị đại diện là

Doanh thu	[5; 7)	[7; 9)	[9; 11)	[11; 13)	[13; 15)
Giá trị đại diện	6	8	10	12	14
Số ngày	2	7	7	3	1

Giá trị trung bình là

$\overline{x}=\frac{2.6+7.8+7.10+3.12+1.14}{20}=9,4$.

Phương sai của mẫu số liệu ghép nhóm trên là

$S^2=\frac{{2.6}^2+{7.8}^2+{7.10}^2+{3.12}^2+{1.14}^2}{20}-9,4^2=4,04$.

Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là

$S=\sqrt{4,04}\approx 2,01$.

Bài 4. Thống kê điểm trung bình môn Toán của một số học sinh lớp 12 được cho ở bảng sau:

Khoảng điểm	[6,5; 7)	[7; 7,5)	[7,5; 8)	[8; 8,5)	[8,5; 9)	[9; 9,5)	[9,5; 10)
Tần số	8	10	16	24	13	7	4

Tính phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm trên.

Hướng dẫn giải

Bảng thông kê có giá trị đại diện

Khoảng điểm	[6,5; 7)	[7; 7,5)	[7,5; 8)	[8; 8,5)	[8,5; 9)	[9; 9,5)	[9,5; 10)
Giá trị đại diện	6,75	7,25	7,75	8,25	8,75	9,25	9,75
Tần số	8	10	16	24	13	7	4

Cỡ mẫu n = 8 + 10 + 16 + 24 + 13 + 7 + 4 = 82.

Giá trị trung bình của mẫu số liệu là

$\overline{x}=\frac{8.6,75+10.7,25+16.7,75+24.8,25+13.8,75+7.9,25+4.9,75}{82}\approx 8,12$.

Phương sai của mẫu số liệu là

$S^2=\frac{8.6,{75}^2+10.7,{25}^2+16.7,{75}^2+24.8,{25}^2+13.8,{75}^2+7.9,{25}^2+4.9,{75}^2}{82}-8,{12}^2\approx 0,64$

Độ lệch chuẩn của mẫu số liệu là

$S=\sqrt{0,64}=0,8$.

Bài 5. Kết quả khảo sát cân nặng của 25 quả bơ ở hai lô hàng A và B cho trong bảng sau:

a) Hãy so sánh cân nặng trung bình của 25 quả bơ của hai lô hàng A và lô hàng B.

b) Nếu so sánh theo độ lệch chuẩn thì cân nặng của 25 quả bơ của lô hàng nào đồng đều hơn?

Hướng dẫn giải

Bảng thống kê có giá trị đại diện

a) Giá trị trung bình của lô A là

$\overline{x_A}=\frac{1.152,5+7.157,5+12.162,5+3.167,5+2.172,5}{25}=162,1$.

Giá trị trung bình của lô B là

$\overline{x_B}=\frac{2.152,5+5.157,5+10.162,5+4.167,5+4.172,5}{25}=163,1$.

Cân nặng trung bình của lô hàng B nặng hơn lô hàng A.

b) Phương sai của lô A

$S_A^2=\frac{1.152,5^2+7.157,5^2+12.162,5^2+3.167,5^2+2.172,5^2}{25}-162,1^2=21,84$.

Độ lệch chuẩn của lô A

$S_A=\sqrt{21,84}\approx 4,67$.

Phương sai của lô B

$S_B^2=\frac{2.152,5^2+5.157,5^2+10.162,5^2+4.167,5^2+4.172,5^2}{25}-163,1^2=32,64$.

Độ lệch chuẩn của lô B

$S_B=\sqrt{32,64}\approx 5,71$.

Vì S_B > S_A nên cân nặng của 25 quả bơ ở lô hàng A thì có sự phân bố đồng đều hơn.

Học tốt Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm

Các bài học để học tốt Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài 2: Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm