Tổng hợp lý thuyết Toán 12 Chương 1 - Chân trời sáng tạo

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Chương 1: Ứng dụng đạo hàm để khảo sát hàm số sách Chân trời sáng tạo hay nhất, chi tiết với bài tập có lời giải sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm Toán 12 Chương 1.

Tổng hợp lý thuyết Toán 12 Chương 1 - Chân trời sáng tạo

Tổng hợp lý thuyết Toán 12 Chương 1

1. Tính đơn điệu và cực trị của hàm số

1.1. Tính đơn điệu của hàm số

* Tính đồng biến, nghịch biến của hàm số

Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K.

- Hàm số y = f(x) gọi là đồng biến (tăng) trên K nếu với mọi x₁, x₂ thuộc K mà x₁ < x₂ thì f(x₁) < f(x₂).

- Hàm số y = f(x) gọi là nghịch biến (giảm) trên K nếu với mọi x₁, x₂ thuộc K mà x₁ < x₂ thì f(x₁) > f(x₂).

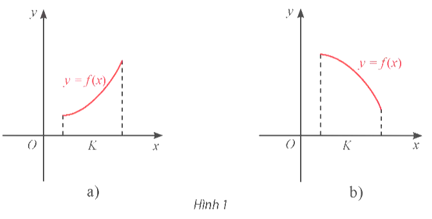
- Nếu hàm số y = f(x) đồng biến trên K thì đồ thị của nó đi lên từ trái sang phải (Hình 1a).

- Nếu hàm số y = f(x) nghịch biến trên K thì đồ thị của nó đi xuống từ trái sang phải (Hình 1b).

- Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K.

• Tính đơn điệu của hàm số

Cho hàm số y = f(x) có đạo hàm trên K.

- Nếu f'(x) > 0 với mọi x thuộc K thì hàm số y = f(x) đồng biến trên K.

- Nếu f'(x) < 0 với mọi x thuộc K thì hàm số y = f(x) nghịch biến trên K.

Chú ý: Khi xét tính đơn điệu của hàm số mà chưa cho khoảng K, ta hiểu xét tính đơn điệu của hàm số đó trên tập xác định của nó.

• Các bước để xét tính đơn điệu của hàm số y = f(x)

Bước 1: Tìm tập xác định D của hàm số.

Bước 2: Tính đạo hàm f'(x) của hàm số. Tìm các điểm x thuộc D mà tại đó đạo hàm f'(x) bằng 0 hoặc đạo hàm không tồn tại.

Bước 3: Xét dấu f'(x) và lập bảng biến thiên.

Bước 4: Nếu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

Chú ý:

a) Nếu hàm số y = f(x) có đạo hàm trên K, f'(x) ≥ 0 với mọi x ∈ K và f'(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên K.

b) Nếu hàm số y = f(x) có đạo hàm trên K, f'(x) ≤ 0 với mọi x ∈ K và f'(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số nghịch biến trên K.

c) Nếu f'(x) = 0 với mọi x ∈ K thì hàm số không đổi trên K.

1.2. Cực trị của hàm số

• Khái niệm cực trị của hàm số

Cho hàm số y = f(x) xác định trên tập hợp D và x₀ ∈ D.

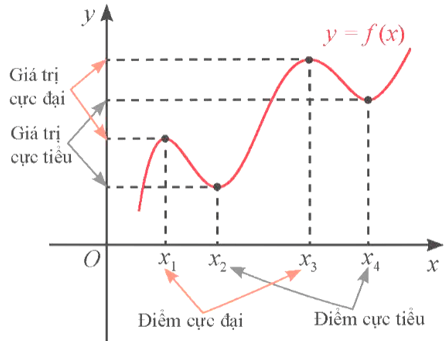
- Nếu tồn tại một khoảng (a; b) chứa điểm x₀ và (a; b) $\subset$ D sao cho f(x) < f(x₀) với mọi x $\in$ (a; b)\{x₀} thì x₀ được gọi là một điểm cực đại, f(x₀) được gọi là giá trị cực đại của hàm số y = f(x), kí hiệu y_CĐ.

- Nếu tồn tại một khoảng (a; b) chứa điểm x₀ và (a; b) $\subset$ D sao cho f(x) > f(x₀) với mọi x $\in$ (a; b)\{x₀}, thì x₀ được gọi là một điểm cực tiểu, f(x₀) được gọi là giá trị cực tiểu của hàm số y = f(x), kí hiệu y_CT.

Chú ý:

a) Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị của hàm số. Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (còn gọi là cực trị) của hàm số.

b) Nếu x₀ là một điểm cực trị (điểm cực đại, điểm cực tiểu) của hàm số y = f(x) thì ta cũng nói hàm số y = f(x) đạt cực trị (cực đại, cực tiểu) tại x₀.

c) Hàm số có thể đạt cực đại và cực tiểu tại nhiều điểm trên D.

d) Nếu x₀ là điểm cực trị của hàm số y = f(x) thì điểm M(x₀; f(x₀)) là một điểm cực trị của đồ thị hàm số y = f(x).

• Cực trị của hàm số

Cho hàm số y = f(x) liên tục trên khoảng (a; b) chứa điểm x₀ và có đạo hàm trên các khoảng (a; x₀) và (x₀; b). Khi đó:

- Nếu f'(x) < 0 với mọi x $\in$ (a; x₀) và f'(x) > 0 với mọi x $\in$ (x₀; b) thì hàm số y = f(x) đạt cực tiểu tại điểm x₀;

- Nếu f'(x) > 0 với mọi x $\in$ (a; x₀) và f'(x) < 0 với mọi x $\in$ (x₀; b) thì hàm số y = f(x) đạt cực đại tại điểm x₀.

• Các bước tìm cực trị của hàm số y = f(x)

Bước 1: Tìm tập xác định D của hàm số.

Bước 2: Tính đạo hàm f'(x) của hàm số. Tìm các điểm x thuộc D mà tại đó đạo hàm f'(x) bằng 0 hoặc đạo hàm không tồn tại.

Bước 3: Lập bảng biến thiên của hàm số.

Bước 4: Từ bảng biến thiên kết luận về cực trị của hàm số.

Chú ý:

a) Nếu f'(x₀) = 0 và f'(x) không đổi dấu khi x qua điểm x₀ thì hàm số không có cực trị tại x₀.

b) Nếu f'(x) không đổi dấu trên khoảng K thì f(x) không có cực trị trên khoảng đó.

2. Giá trị lớn nhất, giá trị nhỏ nhất

2.1. Định nghĩa

Cho hàm số y = f(x) xác định trên tập hợp D.

- Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu f(x) ≤ M với mọi x thuộc D và tồn tại x₀ thuộc D sao cho f(x₀) = M. Kí hiệu $M=\underset{D}{\max }f\left(x\right)$

- Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu f(x) ≥ m với mọi x thuộc D và tồn tại x₀ thuộc D sao cho f(x₀) = m. Kí hiệu $m=\underset{D}{\min }f\left(x\right)$

Chú ý:

- Ta quy ước khi chỉ nói giá trị lớn nhất hay giá trị nhỏ nhất của hàm số y = f(x) (mà không cho rõ tập hợp D) thì ta hiểu đó là giá trị lớn nhất hay giá trị nhỏ nhất của hàm số y = f(x) trên tập xác định của nó.

- Giá trị lớn nhất và giá trị nhỏ nhất của hàm số thường được tìm bằng cách sử dụng đạo hàm và bảng biến thiên.

2.2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn

• Các bước tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [a; b].

Bước 1: Tìm các điểm x₁; x₂; …; x_n thuộc khoảng (a; b) mà tại đó f'(x) bằng 0 hoặc không tồn tại.

Bước 2: Tính f(a); f(x₁); f(x₂); …; f(x_n); f(b).

Bước 3: Gọi M là số lớn nhất và m là số nhỏ nhất trong các giá trị tìm được ở Bước 2. Khi đó: $M=\underset{\left[a;b\right]}{\max }f\left(x\right);m=\underset{\left[a;b\right]}{\min }f\left(x\right)$

3. Đường tiệm cận của đồ thị hàm số

3.1. Đường tiệm cận đứng

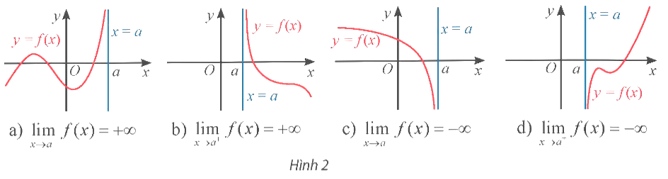
- Đường thẳng x = a được gọi là một đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau thỏa mãn:

$\underset{x\to a^{-}}{\lim }f\left(x\right)=+\infty ,\underset{x\to a^{+}}{\lim }f\left(x\right)=+\infty ,\underset{x\to a^{-}}{\lim }f\left(x\right)=-\infty ,\underset{x\to a^{+}}{\lim }f\left(x\right)=-\infty$

- Đường thẳng x = a là tiệm cận đứng của đồ thị hàm số y = f(x) được minh họa như Hình 2.

3.2. Đường tiệm cận ngang

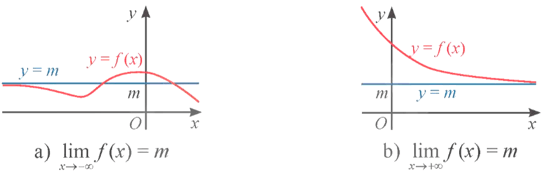
- Đường thẳng y = m được gọi là một đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu $\underset{x\to -\infty }{\lim }f\left(x\right)=m$ hoặc $\underset{x\to +\infty }{\lim }f\left(x\right)=m$

- Đường thẳng y = m là tiệm cận ngang của đồ thị hàm số y = f(x) được minh họa như hình bên dưới.

3.3. Đường tiệm cận xiên

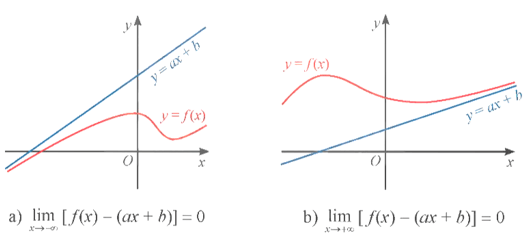
- Đường thẳng y = ax + b, a ≠ 0, được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu $\underset{x\to -\infty }{\lim }\left[f\left(x\right)-\left(ax+b\right)\right]=0$  hoặc $\underset{x\to +\infty }{\lim }\left[f\left(x\right)-\left(ax+b\right)\right]=0$.

- Đường thẳng y = ax + b là tiệm cận xiên của đồ thị hàm số y = f(x) được minh họa như hình sau:

Nhận xét:

a) Trong trường hợp tổng quát, có thể tìm các hệ số a, b trong phương trình của đường tiệm cận xiên y = ax + b theo công thức như sau:

 $a=\underset{x\to +\infty }{\lim }\frac{f\left(x\right)}{x};b=\underset{x\to +\infty }{\lim }\left[f\left(x\right)-ax\right]$ hoặc $a=\underset{x\to -\infty }{\lim }\frac{f\left(x\right)}{x};b=\underset{x\to -\infty }{\lim }\left[f\left(x\right)-ax\right]$.

b) Khi a = 0 thì đồ thị của hàm số có tiệm cận ngang là đường thẳng y = b.

4. Sơ đồ khảo sát hàm số

Để khảo sát và vẽ đồ thị hàm số y = f(x), ta thực hiện theo các bước sau:

Bước 1. Tìm tập xác định của hàm số.

Bước 2. Xét sự biến thiên của hàm số

- Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu, cực trị (nếu có) của hàm số.

- Tìm giới hạn tại vô cực, giới hạn vô cực của hàm số và các đường tiệm cận của đồ thị hàm số (nếu có).

- Lập bảng biến thiên của hàm số.

Bước 3. Vẽ đồ thị của hàm số

- Xác định các điểm cực trị (nếu có), giao điểm của đồ thị với các trục tọa độ (nếu có và dễ tìm), …

- Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).

- Vẽ đồ thị hàm số.

Chú ý: Chỉ ra tâm đối xứng và trục đối xứng của đồ thị hàm số (nếu có).

Bài tập ôn tập Chương 1

1. Bài tập trắc nghiệm

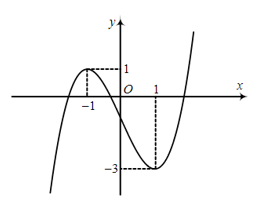
Bài 1. Cho hàm số y = f(x) xác định, liên tục trên ℝ và có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên (−∞; 1).                

B. Hàm số đồng biến trên khoảng (−∞; −1).

C. Hàm số đồng biến trên khoảng (0; +∞).

D. Hàm số đồng biến trên khoảng (−3; +∞).

Hướng dẫn giải

Đáp án đúng là: B

Dựa vào đồ thị hàm số, ta thấy hàm số đồng biến trên khoảng (−∞; −1).

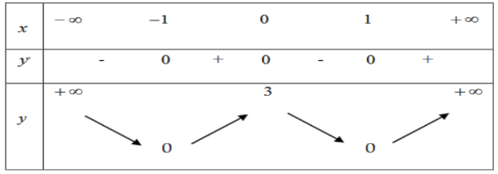
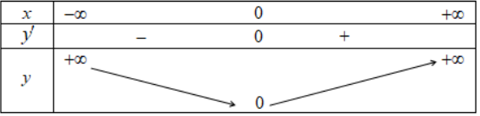
Bài 2. Cho hàm số y = f(x) có bảng biến thiên như sau

Mệnh đề nào dưới đây sai?

A. Hàm số có giá trị cực đại bằng 3.

B. Hàm số có hai điểm cực tiểu.

C. Hàm số có giá trị cực đại bằng 0.

D. Hàm số có 3 điểm cực trị.

Hướng dẫn giải

Đáp án đúng là: C

Dựa vào bảng biến thiên, ta có:

Hàm số đạt cực đại tại x = 0 và y_CĐ = 3.

Hàm số đạt cực tiểu tại x = −1; x = 1 và y_CT = 0.

Do đó đáp án C sai.

Bài 3. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = f(x) = x³ – 3x² + 3 trên đoạn [1; 3]. Giá trị M + m bằng

A. 8.

B. 2.

C. 4.

D. 6.

Hướng dẫn giải

Đáp án đúng là: B

Trên đoạn [1; 3], có y' = 3x² – 6x; y' = 0 $\iff$ x = 0 (loại) hoặc x = 2 (nhận).

Có f(1) = 1; f(2) = −1; f(3) = 3.

Do đó $M=\underset{\left[1;3\right]}{\max }f\left(x\right)=3;m=\underset{\left[1;3\right]}{\min }f\left(x\right)=-1$ .

Vậy M + m = 3 + (−1) = 2.

Bài 4. Giá trị lớn nhất của hàm số $y=f\left(x\right)=\sqrt{3-2x-x^2}$  là

A. 1.

B. 2.

C. 3.

D. 4.

Hướng dẫn giải

Đáp án đúng là: B

Điều kiện: 3 – 2x – x² ≥ 0 $\iff$ −3 ≤ x ≤ 1.

Có $y^{\text{'}}=\frac{-x-1}{\sqrt{3-2x-x^2}}$ ; y' = 0 $\iff$ −x – 1 = 0 $\iff$ x = −1 (nhận).

Có f(−3) = 0; f(−1) = 2; f(1) = 0.

Vậy $\underset{\left[-3;1\right]}{\max }f\left(x\right)=f\left(-1\right)=2$ .

Bài 5. Cho hàm số y = f(x) xác định trên ℝ\{1} và có$\underset{x\to -\infty }{\lim }f\left(x\right)=-2,\underset{x\to 1^{+}}{\lim }f\left(x\right)=+\infty ,\underset{x\to 1^{-}}{\lim }f\left(x\right)=+\infty ,\underset{x\to +\infty }{\lim }f\left(x\right)=2$. Khẳng định nào sau đây đúng?

A. Đồ thị hàm số đã cho có đúng một tiệm cận ngang là đường thẳng y = 1.

B. Đồ thị hàm số đã cho có đúng hai tiệm cận ngang là các đường thẳng y = 2; y = −2.

C. Đồ thị hàm số đã cho có đúng hai tiệm cận đứng là các đường thẳng x = 2 và x = −2.

D. Đồ thị hàm số đã cho không có tiệm cận đứng.

Hướng dẫn giải

Đáp án đúng là: B

Có $\underset{x\to -\infty }{\lim }f\left(x\right)=-2,\underset{x\to 1^{+}}{\lim }f\left(x\right)=+\infty ,\underset{x\to 1^{-}}{\lim }f\left(x\right)=+\infty ,\underset{x\to +\infty }{\lim }f\left(x\right)=2$.

Suy ra y = 2; y = −2 là các tiệm cận ngang của đồ thị hàm số và x = 1 là tiệm cận đứng của đồ thị hàm số.

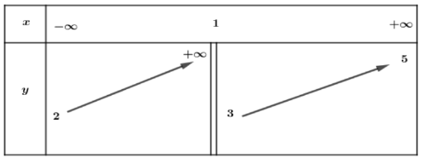
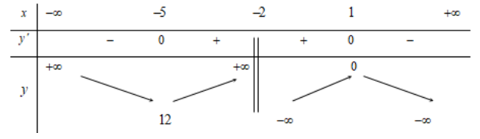
Bài 6. Cho hàm số y = f(x) có bảng biến thiên như sau

Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là

A. 3.

B. 2.

C. 4.

D. 1.

Hướng dẫn giải

Đáp án đúng là: A

Vì $\underset{x\to -\infty }{\lim }f\left(x\right)=2;\underset{x\to +\infty }{\lim }f\left(x\right)=5;\underset{x\to 1^{-}}{\lim }f\left(x\right)=+\infty$  nên đồ thị hàm số có hai tiệm cận ngang là y = 2; y = 5 và một tiệm cận đứng là x = 1.

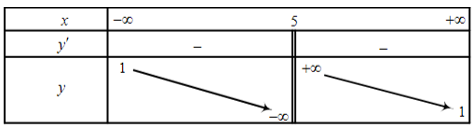
Bài 7. Hàm số nào dưới đây có bảng biến thiên như sau:

A. $y=\frac{x-7}{x-5}$

B. $y=\frac{x-5}{x-1}$

C. $y=\frac{5x}{x-1}$

D. $y=\frac{x-3}{x-5}$

Hướng dẫn giải

Đáp án đúng là: D

Dựa vào bảng biến thiên ta thấy:

+)  x = 5 là tiệm cận đứng và y = 1 là tiệm cận ngang của đồ thị hàm số. Do đó loại B và C.

+) Hàm số nghịch biến trên (−∞; 5) và (5; +∞).

Xét đáp án A. Có $y^{\text{'}}=\frac{2}{{\left(x-5\right)}^2}>0,\forall x\ne 5$  nên loại đáp án A.

Xét đáp án D. Có $y^{\text{'}}=\frac{-2}{{\left(x-5\right)}^2}<0,\forall x\ne 5$ . Do đó chọn đáp án D.

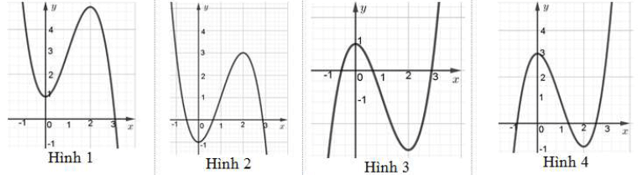
Bài 8. Đồ thị của hàm số y = −x³ + 3x² – 1 là hình nào dưới đây

A. Hình 1.

B. Hình 2.

C. Hình 3.

D. Hình 4.

Hướng dẫn giải

Đáp án đúng là: B

Vì đồ thị hàm số y = −x³ + 3x² – 1 cắt trục tung tại (0; −1). Do đó chọn B.

2. Bài tập tự luận

Bài 1. Xét tính đơn điệu của các hàm số sau:

a) y = x⁴ + 4x²;

b) $y=\frac{-x^2+2x-1}{x+2}$

Hướng dẫn giải

a) Tập xác định: D = ℝ.

Có y' = 4x³ + 8x; y' = 0 $\iff$ x = 0.

Bảng biến thiên

Vậy hàm số đồng biến trên khoảng (0; +∞) và nghịch biến trên khoảng (−∞; 0).

b) Tập xác định: D = ℝ\{−2}.

Có $y^{\text{'}}=\frac{\left(-2x+2\right)\left(x+2\right)-\left(-x^2+2x-1\right)}{{\left(x+2\right)}^2}=\frac{-x^2-4x+5}{{\left(x+2\right)}^2}$ .

Có y' = 0 $\iff$ −x² – 4x + 5 = 0 $\iff$ x = 1 hoặc x = −5.

Bảng biến thiên

Vậy hàm số nghịch biến trên các khoảng (−∞; −5) và (1; +∞).

Hàm số đồng biến trên các khoảng (−5; −2) và (−2; 1).

Bài 2. Tìm cực trị của các hàm số sau

a) y = x³ – 6x² + 9x;

b) $y=\frac{2x-2}{x+1}$

Hướng dẫn giải

a) Tập xác định: D = ℝ.

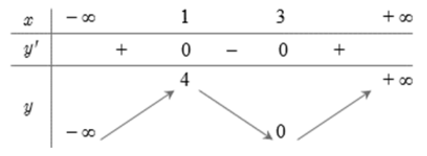
Có y' = 3x² – 12x + 9; y' = 0 $\iff$ x = 1 hoặc x = 3.

Bảng biến thiên

Vậy hàm số đạt cực đại tại x = 1 và y_CĐ = 4.

Hàm số đạt cực tiểu tại x = 3 và y_CT = 0.

b) Tập xác định: D = ℝ\{−1}.

Có $y^{\text{'}}=\frac{2\left(x+1\right)-\left(2x-2\right)}{{\left(x+1\right)}^2}=\frac{4}{{\left(x+1\right)}^2}>0,\forall x\ne -1$.

Do đó hàm số luôn đồng biến trên các khoảng (−∞; −1) và (−1; +∞).

Hàm số không có cực trị.

Bài 3. Thể tích nước của một bể bơi sau t phút bơm tính theo công thức $V\left(t\right)=\frac{1}{100}\left(30t^3-\frac{t^4}{4}\right)$, (0 ≤ t ≤ 90). Tốc độ bơm nước tại thời điểm t được tính bởi f(t) = V'(t). Trong khoảng thời gian nào tốc độ bơm tăng? Trong khoảng thời gian nào tốc độ bơm giảm?

Hướng dẫn giải

Với 0 ≤ t ≤ 90,

Có $f\left(t\right)=V^{\text{'}}\left(t\right)=\frac{9}{10}{t}^2-\frac{1}{100}{t}^3$.

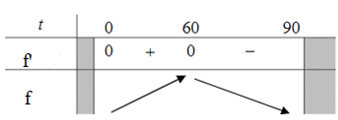
Có $f^{\text{'}}\left(t\right)=V^{\text{'}\text{'}}\left(t\right)=\frac{9}{5}t-\frac{3}{100}{t}^2$; f'(t) = 0 $\iff$ t = 0 hoặc t = 60.

Bảng biến thiên

Dựa vào bảng biến thiên ta thấy:

Tốc độ bơm tăng từ phút 0 đến phút 60, tốc độ bơm giảm từ phút 60 đến phút 90.

Bài 4. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y=f\left(x\right)=\frac{-x^2-4}{x}$  trên đoạn $\left[\frac{3}{2};4\right]$.

Hướng dẫn giải

Trên đoạn $\left[\frac{3}{2};4\right]$ , có $y^{\text{'}}=\frac{-2x^2-\left(-x^2-4\right)}{x^2}=\frac{-x^2+4}{x^2}$;

y' = 0 $\iff$ −x² + 4 = 0 $\iff$ x = −2 (loại) hoặc x = 2 (nhận).

Có $f\left(\frac{3}{2}\right)=-\frac{25}{6}$ ; f(2) = −4; f(4) = −5.

Vậy $\underset{\left[\frac{3}{2};4\right]}{\max }f\left(x\right)=f\left(2\right)=-4;\underset{\left[\frac{3}{2};4\right]}{\min }f\left(x\right)=f\left(4\right)=-5$.

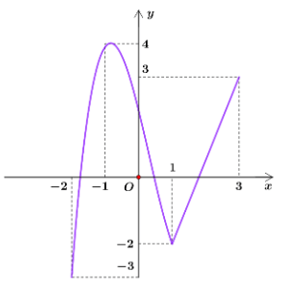
Bài 5. Cho hàm số f(x) liên tục trên đoạn [−2; 3] có đồ thị như hình vẽ dưới đây. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số trên đoạn [−2; 3]. Giá trị của 2m – 3M bằng bao nhiêu?

Hướng dẫn giải

Dựa vào đồ thị ta có: $m=\underset{\left[-2;3\right]}{\min }f\left(x\right)=-3;M=\underset{\left[-2;3\right]}{\max }f\left(x\right)=4$.

Do đó 2m – 3M = 2.(−3) – 3.4 = −18.

Bài 6. Hằng ngày mực nước của hồ thủy điện ở miền Trung lên và xuống theo lượng nước mưa và các suối nước đổ về hồ. Từ lúc 8 giờ sáng, độ sâu của mực nước trong hồ tính theo mét và lên xuống theo thời gian t (giờ) trong ngày cho bởi công thức: $h\left(t\right)=-\frac{1}{3}{t}^3+5t^2+24t\left(t>0\right)$. Biết rằng cần phải thông báo cho các hộ dân phải di dời trước khi xả nước theo quy định trước 5 giờ. Hỏi cần thông báo cho hộ dân di dời trước khi xả nước lúc mấy giờ. Biết rằng mực nước trong hồ phải lên cao nhất mới xả nước.

Hướng dẫn giải

Xét hàm số $h\left(t\right)=-\frac{1}{3}{t}^3+5t^2+24t\left(t>0\right)$.

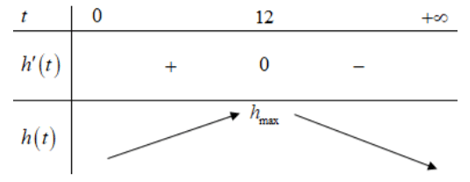
Có h'(t) = −t² + 10t + 24; h'(t) = 0 $\iff$ t = −2 (loại) hoặc t = 12 (nhận).

Bảng biến thiên

Dựa vào bảng biến thiên ta thấy để mực nước dâng cao nhất thì phải mất 12 giờ. Do đó phải thông báo cho người dân di dời vào 15 giờ chiều cùng ngày.

Bài 7. Tìm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số sau

a) $y=\frac{2x-1}{2x+4}$

b) $y=\frac{3x+2}{x-2}$

Hướng dẫn giải

a) Tập xác định: D = ℝ\{−2}.

Có $\underset{x\to {\left(-2\right)}^{-}}{\lim }\frac{2x-1}{2x+4}=+\infty ;\underset{x\to {\left(-2\right)}^{+}}{\lim }\frac{2x-1}{2x+4}=-\infty$.

Do đó x = −2 là tiệm cận đứng của đồ thị hàm số.

Có $\underset{x\to +\infty }{\lim }\frac{2x-1}{2x+4}=\underset{x\to +\infty }{\lim }\frac{2-\frac{1}{x}}{2+\frac{4}{x}}=1$; $\underset{x\to -\infty }{\lim }\frac{2x-1}{2x+4}=\underset{x\to -\infty }{\lim }\frac{2-\frac{1}{x}}{2+\frac{4}{x}}=1$.

Do đó y = 1 là tiệm cận ngang của đồ thị hàm số.

b) Tập xác định: D = ℝ\{2}.

Có $\underset{x\to 2^{+}}{\lim }\frac{3x+2}{x-2}=+\infty ;\underset{x\to 2^{-}}{\lim }\frac{3x+2}{x-2}=-\infty$.

Do đó x = 2 là tiệm cận đứng của đồ thị hàm số.

Có $\underset{x\to +\infty }{\lim }\frac{3x+2}{x-2}=3;\underset{x\to -\infty }{\lim }\frac{3x+2}{x-2}=3$.

Do đó y = 3 là tiệm cận ngang của đồ thị hàm số.

Bài 8. Tìm tiệm cận đứng và tiệm cận xiên của đồ thị hàm số sau

a) $y=f\left(x\right)=\frac{x^2-x-1}{x-1}$

b) $y=f\left(x\right)=\frac{2x^2+3x+2}{x+1}$

Hướng dẫn giải

a) Tập xác định: D = ℝ\{1}.

Có $\underset{x\to 1^{+}}{\lim }\frac{x^2-x-1}{x-1}=-\infty ;\underset{x\to 1^{-}}{\lim }\frac{x^2-x-1}{x-1}=+\infty$ .

Do đó x = 1 là tiệm cận đứng của đồ thị hàm số.

Có $a=\underset{x\to +\infty }{\lim }\frac{f\left(x\right)}{x}=\underset{x\to +\infty }{\lim }\frac{x^2-x-1}{x^2-x}=1$;

$b=\underset{x\to +\infty }{\lim }\left[f\left(x\right)-x\right]=\underset{x\to +\infty }{\lim }\left[\frac{x^2-x-1}{x-1}-x\right]=\underset{x\to +\infty }{\lim }\left(-\frac{1}{x-1}\right)=0$.

Tương tự $a=\underset{x\to -\infty }{\lim }\frac{f\left(x\right)}{x}=1$; $b=\underset{x\to -\infty }{\lim }\left[f\left(x\right)-x\right]=0$.

Do đó y = x là tiệm cận xiên của đồ thị hàm số.

b) Tập xác định: D = ℝ\{−1}.

Có $\underset{x\to {\left(-1\right)}^{-}}{\lim }\frac{2x^2+3x+2}{x+1}=-\infty ;\underset{x\to {\left(-1\right)}^{+}}{\lim }\frac{2x^2+3x+2}{x+1}=+\infty$.

Do đó x = −1 là tiệm cận đứng của đồ thị hàm số.

Có $a=\underset{x\to +\infty }{\lim }\frac{f\left(x\right)}{x}=\underset{x\to +\infty }{\lim }\frac{2x^2+3x+2}{x^2+x}=2$;

$b=\underset{x\to +\infty }{\lim }\left[f\left(x\right)-2x\right]=\underset{x\to +\infty }{\lim }\left[\frac{2x^2+3x+2}{x+1}-2x\right]=\underset{x\to +\infty }{\lim }\frac{x+2}{x-1}=1$.

Tương tự $a=\underset{x\to -\infty }{\lim }\frac{f\left(x\right)}{x}=2$; $b=\underset{x\to -\infty }{\lim }\left[f\left(x\right)-2x\right]=1$.

Do đó y = 2x + 1 là tiệm cận xiên của đồ thị hàm số.

Bài 9. Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được tính theo công thức $c\left(t\right)=\frac{t}{t^2+1}$(mg/l). Tìm các đường tiệm cận của đồ thị hàm số y = c(t).

Hướng dẫn giải

Tập xác định: D = (0; +∞).

$\underset{t\to +\infty }{\lim }c\left(t\right)=\underset{t\to +\infty }{\lim }\frac{t}{t^2+1}=0$.

Do đó y = 0 là tiệm cận ngang của đồ thị hàm số.

Đồ thị hàm số không có tiệm cận đứng.

Bài 10. Khảo sát và vẽ đồ thị của hàm số

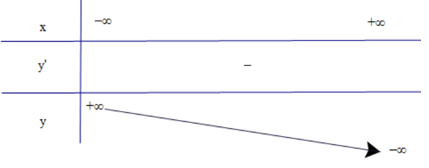
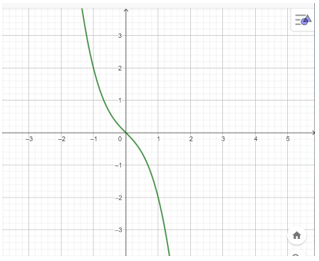
a) y = −x³ – x;

b) $y=\frac{-x+3}{x-1}$

Hướng dẫn giải

a) y = −x³ – x

1. Tập xác định: D = ℝ.

2. Sự biến thiên

• Chiều biến thiên

Có y’ = −3x² – 1 < 0, ∀x ∈ ℝ.

Do đó hàm số luôn nghịch biến.

Hàm số đã cho không có cực trị.

• Các giới hạn tại vô cực

$\underset{x\to +\infty }{\lim }\left(-x^3-x\right)=\underset{x\to +\infty }{\lim }{x}^3\left(-1-\frac{1}{x^2}\right)=-\infty$; $\underset{x\to -\infty }{\lim }\left(-x^3-x\right)=\underset{x\to -\infty }{\lim }{x}^3\left(-1-\frac{1}{x^2}\right)=+\infty$.

• Bảng biến thiên

3. Đồ thị

Đồ thị hàm số đi qua gốc tọa độ và điểm (1; −2).

Đồ thị hàm số nhận (0; 0) làm tâm đối xứng.

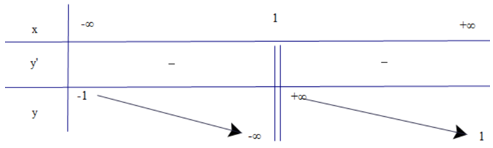
b) $y=\frac{-x+3}{x-1}$

1. Tập xác định: D = ℝ\{1}.

2. Sự biến thiên

• Chiều biến thiên

Có $y^{\text{'}}=-\frac{2}{{\left(x-1\right)}^2}<0,\forall x\ne 1$.

Hàm số nghịch biến trên các khoảng (−∞; 1) và (1; +∞).

Hàm số không có cực trị

• Tiệm cận

Có $\underset{x\to 1^{-}}{\lim }y=\underset{x\to 1^{-}}{\lim }\frac{-x+3}{x-1}=-\infty ;\underset{x\to 1^{+}}{\lim }y=\underset{x\to 1^{+}}{\lim }\frac{-x+3}{x-1}=+\infty$.

Do đó x = 1 là tiệm cận đứng của đồ thị hàm số.

Có $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{-x+3}{x-1}=-1$; $\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{-x+3}{x-1}=-1$.

Do đó y = −1 là tiệm cận ngang của đồ thị hàm số.

• Bảng biến thiên

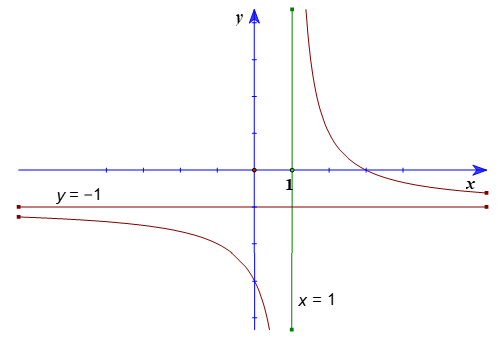
3. Đồ thị

Đồ thị hàm số giao với Ox tại (3; 0) và giao với Oy tại (0; −3).

Tâm đối xứng của đồ thị là (1; −1).

Các trục đối xứng của đồ thị là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = 1 và y = −1.

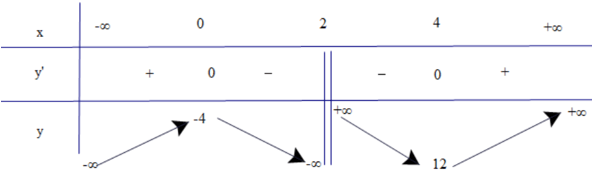
Bài 11. Khảo sát và vẽ đồ thị của hàm số $y=\frac{2x^2-4x+8}{x-2}$.

Hướng dẫn giải

1. Tập xác định: D = ℝ\{2}.

2. Sự biến thiên

• Chiều biến thiên

Có $y^{\text{'}}=\frac{\left(4x-4\right)\left(x-2\right)-\left(2x^2-4x+8\right)}{{\left(x-2\right)}^2}=\frac{2x^2-8x}{{\left(x-2\right)}^2}$;

y' = 0 Û 2x² – 8x = 0 $\iff$ x = 0 hoặc x = 4.

Trên các khoảng (−∞; 0) và (4; +∞), có y' > 0 nên hàm số đồng biến trên mỗi khoảng đó.

Trên các khoảng (0; 2) và (2; 4), có y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó.

• Cực trị

Hàm số đạt cực đại tại x = 0 và y_CĐ = −4.

Hàm số đạt cực tiểu tại x = 4 và y_CT = 12.

• Giới hạn và tiệm cận

$\underset{x\to +\infty }{\lim }y=\underset{x\to +\infty }{\lim }\frac{2x^2-4x+8}{x-2}=+\infty ;$ $\underset{x\to -\infty }{\lim }y=\underset{x\to -\infty }{\lim }\frac{2x^2-4x+8}{x-2}=-\infty$.

Có $\underset{x\to 2^{-}}{\lim }y=\underset{x\to 2^{-}}{\lim }\frac{2x^2-4x+8}{x-2}=-\infty ;\underset{x\to 2^{+}}{\lim }y=\underset{x\to 2^{+}}{\lim }\frac{2x^2-4x+8}{x-2}=+\infty$.

Do đó x = 2 là tiệm cận đứng của đồ thị hàm số.

Có $a=\underset{x\to +\infty }{\lim }\frac{2x^2-4x+8}{x^2-2x}=2; b=\underset{x\to +\infty }{\lim }\left(\frac{2x^2-4x+8}{x-2}-2x\right)=\underset{x\to +\infty }{\lim }\frac{8}{x-2}=0$.

Tương tự$a=\underset{x\to -\infty }{\lim }\frac{2x^2-4x+8}{x^2-2x}=2; b=\underset{x\to -\infty }{\lim }\left(\frac{2x^2-4x+8}{x-2}-2x\right)=\underset{x\to -\infty }{\lim }\frac{8}{x-2}=0$.

Do đó y = 2x là tiệm cận xiên của đồ thị hàm số.

• Bảng biến thiên

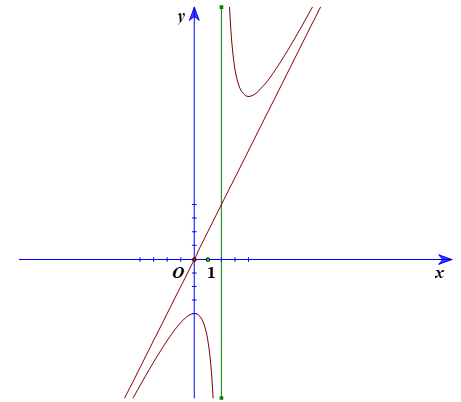
3. Đồ thị

Đồ thị hàm số giao với Oy tại (0; −4).

Tâm đối xứng của đồ thị hàm số là (2; 4).

Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = 2 và y = 2x.

Bài 12. Một tên lửa bay vào không trung với quãng đường đi được s(t) (km) là hàm phụ thuộc theo biến t (giây) theo quy tắc sau: $s\left(t\right)=e^{t^2+3}+2t{e}^{3t+1}$(km). Hỏi vận tốc của tên lửa sau 1 giây là bao nhiêu (biết hàm biểu thị vận tốc là đạo hàm của hàm biểu thị quãng đường theo thời gian).

Hướng dẫn giải

Ta có $v\left(t\right)=s^{\text{'}}\left(t\right)=2t{e}^{t^2+3}+2e^{3t+1}+6t{e}^{3t+1}$.

Vận tốc của tên lửa sau 1 giây là: $v\left(1\right)=2e^{1^2+3}+2e^{3.1+1}+6e^{3.1+1}=10e^4$(km/s).

Học tốt Chương 1

Các bài học để học tốt Bài tập cuối chương 1 Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài tập cuối chương 1