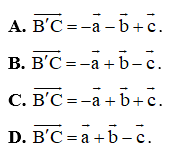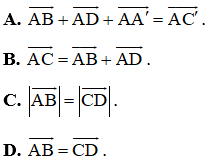Lý thuyết Toán lớp 12 Vectơ và các phép toán trong không gian - Chân trời sáng tạo

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Bài 1: Vectơ và các phép toán trong không gian sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán lớp 12 Vectơ và các phép toán trong không gian - Chân trời sáng tạo

Lý thuyết Vectơ và các phép toán trong không gian

A. Lý thuyết

1. Vectơ trong không gian

● Định nghĩa

Vectơ trong không gian là một đoạn thẳng có hướng.

Chú ý:

- Kí hiệu $\overrightarrow{AB}$ chỉ vectơ có điểm đầu A, điểm cuối B.

- Nếu không cần chỉ rõ điểm đầu và điểm cuối thì vectơ còn được kí hiệu là $\overrightarrow{u},\overrightarrow{v},\overrightarrow{x},\overrightarrow{y},\mathrm{...}$

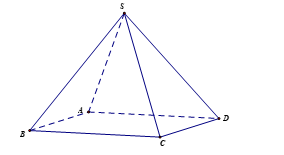
Ví dụ 1. Cho hình chóp S.ABCD. Hãy chỉ ra các vectơ có điểm đầu là S và điểm cuối là các đỉnh còn lại của hình chóp.

Hướng dẫn giải

Ta có 4 vectơ $\overrightarrow{SA},\overrightarrow{SB},\overrightarrow{SC},\overrightarrow{SD}$ có điểm đầu là S và điểm cuối là các đỉnh còn lại của hình chóp.

• Trong không gian, các khái niệm có liên quan đến vectơ như giá của vectơ; độ dài của vectơ; hai vectơ cùng phương, cùng hướng, ngược hướng, bằng nhau, đối nhau; vectơ-không được định nghĩa tương tự như trong mặt phẳng.

Chú ý: Trong không gian, cho điểm O và vectơ $\overrightarrow{a}$, tồn tại duy nhất điểm M để $\overrightarrow{OM}=\overrightarrow{a}.$

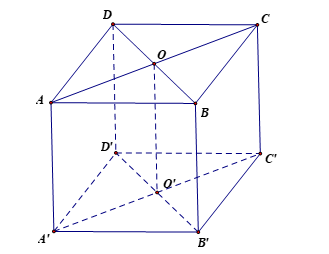
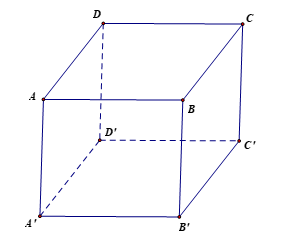
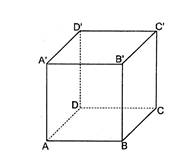
Ví dụ 2. Cho hình lập phương ABCD.A'B'C'D'. Gọi O, O' lần lượt là các giao điểm của hai đường chéo của hai đáy. Hãy xác định các vectơ (khác $\overrightarrow{0}$) có điểm đầu, điểm cuối là các đỉnh của hình lập phương ABCD.A'B'C'D' sao cho

a) bằng $\overrightarrow{O{O}^{\text{'}}}$

b) bằng $\overrightarrow{AC}$

Hướng dẫn giải

a) Các vectơ bằng vectơ $\overrightarrow{O{O}^{\text{'}}}$ là $\overrightarrow{A{A}^{\text{'}}}=\overrightarrow{B{B}^{\text{'}}}=\overrightarrow{C{C}^{\text{'}}}=\overrightarrow{D{D}^{\text{'}}}=\overrightarrow{O{O}^{\text{'}}}$ vì chúng cùng hướng và cùng độ dài với vectơ $\overrightarrow{O{O}^{\text{'}}}$.

b) Vì $\overrightarrow{AC}$ và $\overrightarrow{A^{\text{'}}{C}^{\text{'}}}$ cùng hướng và cùng độ dài nên $\overrightarrow{AC}=\overrightarrow{A^{\text{'}}{C}^{\text{'}}}$.

2. Tổng và hiệu của hai vectơ

• Tổng của hai vectơ

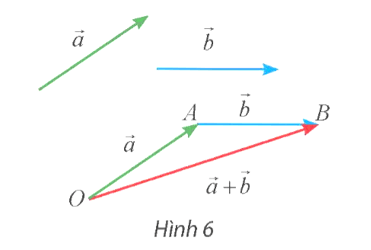
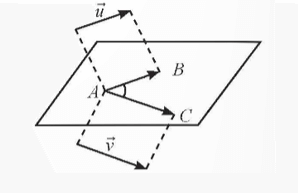
Trong không gian, cho hai vectơ $\overrightarrow{a},\overrightarrow{b}$. Lấy điểm O bất kì và hai điểm A, B sao cho $\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{AB}=\overrightarrow{b}$. Ta gọi $\overrightarrow{OB}$ là tổng của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$, kí hiệu $\overrightarrow{a}+\overrightarrow{b}$.

Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.

Nhận xét: Phép cộng vectơ trong không gian cũng có các tính chất như phép cộng vectơ trong mặt phẳng.

+) Tính chất giao hoán: $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}$;

+) Tính chất kết hợp: $\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}=\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)$;

+) Với mọi vectơ $\overrightarrow{a}$, ta luôn có $\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{a}=\overrightarrow{a}$.

Chú ý: Từ tính chất kết hợp, ta có thể xác định được tổng của ba vectơ $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ là $\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}=\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}$.

• Quy tắc ba điểm, quy tắc hình bình hành

Quy tắc ba điểm, quy tắc hình bình hành vẫn đúng với các vectơ trong không gian.

+) Với ba điểm A, B, C ta có $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.

+) Nếu ABCD là hình bình hành thì ta có $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$.

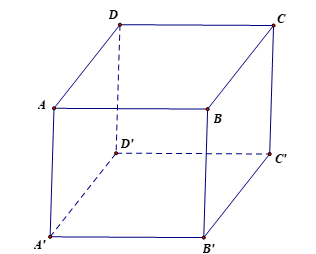
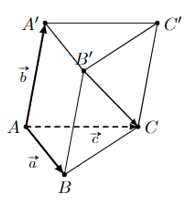
Ví dụ 3. Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng

a) $\overrightarrow{BD}+\overrightarrow{D{D}^{\text{'}}}+\overrightarrow{D^{\text{'}}{B}^{\text{'}}}=\overrightarrow{B{B}^{\text{'}}}$;

b) $\overrightarrow{AC}+\overrightarrow{B{A}^{\text{'}}}+\overrightarrow{DB}+\overrightarrow{C^{\text{'}}D}=\overrightarrow{0}$

Hướng dẫn giải

a) $\overrightarrow{BD}+\overrightarrow{D{D}^{\text{'}}}+\overrightarrow{D^{\text{'}}{B}^{\text{'}}}=\overrightarrow{B{D}^{\text{'}}}+\overrightarrow{D^{\text{'}}{B}^{\text{'}}}=\overrightarrow{B{B}^{\text{'}}}$.

b) $\overrightarrow{AC}+\overrightarrow{B{A}^{\text{'}}}+\overrightarrow{DB}+\overrightarrow{C^{\text{'}}D}=$$\overrightarrow{AC}+\overrightarrow{C^{\text{'}}D}+\overrightarrow{DB}+\overrightarrow{B{A}^{\text{'}}}=$$\overrightarrow{AC}+\overrightarrow{C^{\text{'}}D}+\overrightarrow{D{A}^{\text{'}}}$$=\overrightarrow{AC}+\overrightarrow{C^{\text{'}}{A}^{\text{'}}}=0$.

• Quy tắc hình hộp

Cho hình hộp ABCD.A'B'C'D'. Ta có : $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}^{\text{'}}}=\overrightarrow{A{C}^{\text{'}}}$.

Ví dụ 4. Cho hình hộp ABCD.A'B'C'D'. Tìm giá trị của k thích hợp điền vào đẳng thức vectơ: $\overrightarrow{AB}+\overrightarrow{B^{\text{'}}{C}^{\text{'}}}+\overrightarrow{D{D}^{\text{'}}}=k\overrightarrow{A{C}^{\text{'}}}$.

Hướng dẫn giải

Ta có $\overrightarrow{AD}=\overrightarrow{B^{\text{'}}{C}^{\text{'}}}$; $\overrightarrow{D{D}^{\text{'}}}=\overrightarrow{A{A}^{\text{'}}}$.

Suy ra $\overrightarrow{AB}+\overrightarrow{B^{\text{'}}{C}^{\text{'}}}+\overrightarrow{D{D}^{\text{'}}}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}^{\text{'}}}=\overrightarrow{A{C}^{\text{'}}}=k\overrightarrow{A{C}^{\text{'}}}$.

Do đó k = 1.

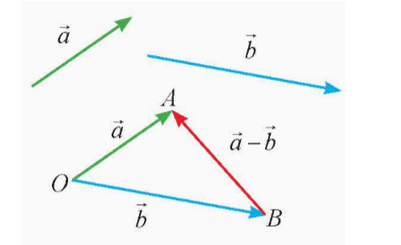
• Hiệu hai vectơ

Trong không gian, cho hai vectơ $\overrightarrow{a},\overrightarrow{b}$. Ta gọi $\overrightarrow{a}+\left(-\overrightarrow{b}\right)$ là hiệu của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$, kí hiệu $\overrightarrow{a}-\overrightarrow{b}$.

Phép lấy hiệu của hai vectơ được gọi là phép trừ vectơ.

• Quy tắc hiệu

Trong không gian, với ba điểm A, B, C ta có: $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$.

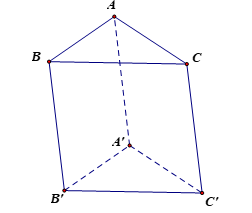
Ví dụ 5. Cho hình lăng trụ tam giác ABC.A'B'C'. Tìm vectơ $\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{BC}$.

Hướng dẫn giải

Ta có $\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{BC}$$=\overrightarrow{CB}+\overrightarrow{BC}=\overrightarrow{0}$ (do $\overrightarrow{BC}$ và $\overrightarrow{CB}$ là hai vectơ đối nhau).

3. Tích của một số với một vectơ

•  Định nghĩa

Trong không gian, cho số thực k ≠ 0 và vectơ $\overrightarrow{a}\ne \overrightarrow{0}$.

Tích của số k với vectơ $\overrightarrow{a}$ là một vectơ, kí hiệu $k\overrightarrow{a}$, cùng hướng với > nếu k > 0, ngược hướng với nếu k < 0 và có độ dài bằng $\left|k\right|.\left|\overrightarrow{a}\right|$.

Phép lấy tích của một số với một vectơ được gọi là phép nhân một số với một vectơ.

Quy ước: $0.\overrightarrow{a}=\overrightarrow{0}$ và $k.\overrightarrow{0}=\overrightarrow{0}$.

Nhận xét:

a) Với hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bất kì, với mọi số h và k, ta có:

+) $k\left(\overrightarrow{a}+\overrightarrow{b}\right)=k\overrightarrow{a}+k\overrightarrow{b}$;

+) $\left(h+k\right)\overrightarrow{a}=h\overrightarrow{a}+k\overrightarrow{a}$;

+) $h\left(k\overrightarrow{a}\right)=\left(hk\right)\overrightarrow{a}$

+) $1.\overrightarrow{a}=\overrightarrow{a}$;

+) $\left(-1\right).\overrightarrow{a}=-\overrightarrow{a}$.

b) $k\overrightarrow{a}=\overrightarrow{0}\iff \overrightarrow{a}=\overrightarrow{0}$ hoặc k = 0.

c) Hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ ($\overrightarrow{b}$ khác $\overrightarrow{0}$) cùng phương khi và chỉ khi có số k sao cho $\overrightarrow{a}=k\overrightarrow{b}$.

d) Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k khác 0 để $\overrightarrow{AB}=k\overrightarrow{AC}$.

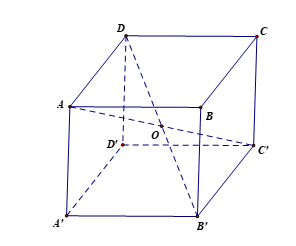
Ví dụ 6. Cho hình lập phương ABCD.A'B'C'D'. Gọi O là tâm của hình lập phương. Chứng minh $\overrightarrow{AO}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}^{\text{'}}}\right)$ .

Hướng dẫn giải

Vì O là tâm hình lập phương nên $\overrightarrow{AO}=\frac{1}{2}\overrightarrow{A{C}^{\text{'}}}$ .

Lại có $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}^{\text{'}}}=\overrightarrow{A{C}^{\text{'}}}$ (theo quy tắc hình hộp).

Do đó $\overrightarrow{AO}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}^{\text{'}}}\right)$.

4. Tích vô hướng của hai vectơ

• Góc giữa hai vectơ trong không gian

Trong không gian, cho $\overrightarrow{u}$ và $\overrightarrow{v}$ là hai vectơ khác $\overrightarrow{0}$. Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho $\overrightarrow{AB}=\overrightarrow{u},\overrightarrow{AC}=\overrightarrow{v}$ . Khi đó, ta gọi $\widehat{BAC}$là góc giữa hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$, kí hiệu $\left(\overrightarrow{u},\overrightarrow{v}\right)$.

Nhận xét:

+) $0°\le \left(\overrightarrow{u},\overrightarrow{v}\right)\le 180°$;

+) Nếu $\left(\overrightarrow{u},\overrightarrow{v}\right)=90°$thì ta nói $\overrightarrow{u}$và $\overrightarrow{v}$ vuông góc với nhau, kí hiệu $\overrightarrow{u}\perp \overrightarrow{v}$.

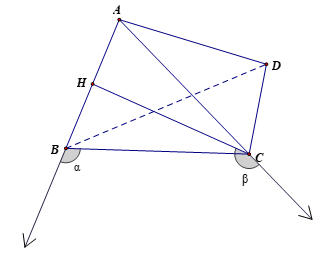
Ví dụ 7. Cho tứ diện đều ABCD có H là trung điểm của cạnh AB. Hãy tính góc giữa các cặp vectơ sau đây:

a) $\overrightarrow{AB}$và $\overrightarrow{BC}$;

b) $\overrightarrow{CH}$ và $\overrightarrow{AC}$.

Hướng dẫn giải

Tứ diện ABCD đều có các mặt là tam giác đều.

a) Ta có $\left(\overrightarrow{AB},\overrightarrow{BC}\right)=\alpha$ .

Mà α = 180° − 60° = 120°.

b) $\left(\overrightarrow{CH},\overrightarrow{AC}\right)=\beta$ .

Vì DACB đều có CH là trung tuyến nên CH đồng thời là đường cao.

Do đó $\widehat{HAC}+\widehat{ACH}=90°$$\Rightarrow \widehat{ACH}=90°-60°=30°$.

Vậy β = 180° − 30° = 150°.

• Tích vô hướng của hai vectơ

Trong không gian, cho hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$  khác $\overrightarrow{0}$ .

Tích vô hướng của hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ là một số, kí hiệu $\overrightarrow{u}.\overrightarrow{v}$ , được xác định bởi công thức $\overrightarrow{u}.\overrightarrow{v}=\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|.\cos \left(\overrightarrow{u},\overrightarrow{v}\right)$ .

Chú ý:

a) Trong trường hợp $\overrightarrow{u}=\overrightarrow{0}$ hoặc $\overrightarrow{v}=\overrightarrow{0}$, ta quy ước .

b) $\overrightarrow{u}.\overrightarrow{u}={\overrightarrow{u}}^2={\left|\overrightarrow{u}\right|}^2;{\overrightarrow{u}}^2\ge 0;{\overrightarrow{u}}^2=0\iff \overrightarrow{u}=\overrightarrow{0}$.

c) Với hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ khác $\overrightarrow{0}$, ta có $\cos \left(\overrightarrow{u},\overrightarrow{v}\right)=\frac{\overrightarrow{u}.\overrightarrow{v}}{\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|}$.

d) Với hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ khác $\overrightarrow{0}$, ta có $\overrightarrow{u}\perp \overrightarrow{v}\iff \overrightarrow{u}.\overrightarrow{v}=0$.

Nhận xét: Tương tự như trong mặt phẳng, tích vô hướng của hai vectơ trong không gian cũng có các tính chất sau:

Với ba vectơ $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ và số k, ta có:

+) $\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{a}$;

+) $\overrightarrow{a}.\left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{a}.\overrightarrow{c}$;

+) $\left(k\overrightarrow{a}\right).\overrightarrow{b}=k\left(\overrightarrow{a}.\overrightarrow{b}\right)=\overrightarrow{a}.\left(k\overrightarrow{b}\right)$.

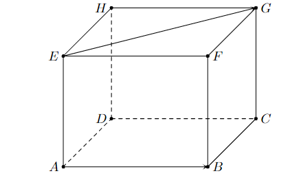
Ví dụ 8. Cho hình lập phương ABCD.EFGH có các cạnh bằng a, khi đó $\overrightarrow{AB}.\overrightarrow{EG}$ bằng

Hướng dẫn giải

Ta có $\overrightarrow{EF}=\overrightarrow{AB},\overrightarrow{FG}=\overrightarrow{BC}$.

Ta có $\overrightarrow{AB}.\overrightarrow{EG}$$=\overrightarrow{AB}.\left(\overrightarrow{EF}+\overrightarrow{FG}\right)$$=\overrightarrow{AB}.\left(\overrightarrow{AB}+\overrightarrow{BC}\right)$$={\overrightarrow{AB}}^2+\overrightarrow{AB}.\overrightarrow{BC}=A{B}^2=a^2$

Vì $\overrightarrow{AB}\perp \overrightarrow{BC}$ nên $\overrightarrow{AB}.\overrightarrow{BC}=0$.

Bài tập Vectơ và các phép toán trong không gian

Bài 1. Cho hình lăng trụ ABC.A'B'C'. Đặt $\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{A{A}^{\text{'}}}=\overrightarrow{b},\overrightarrow{AC}=\overrightarrow{c}$. Khẳng định nào sau đây đúng?

A. $\overrightarrow{B^{\text{'}}C}=-\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$.

B. $\overrightarrow{B^{\text{'}}C}=-\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$.

C. $\overrightarrow{B^{\text{'}}C}=-\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$ .

D. $\overrightarrow{B^{\text{'}}C}=\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}$.

Hướng dẫn giải

Đáp án đúng là: A

Ta có $\overrightarrow{B^{\text{'}}C}=\overrightarrow{BC}-\overrightarrow{B{B}^{\text{'}}}$$=\left(\overrightarrow{AC}-\overrightarrow{AB}\right)-\overrightarrow{B{B}^{\text{'}}}$$=\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b}$.

Bài 2. Cho hình lập phương . Mệnh đề nào sau đây sai?

A. $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}^{\text{'}}}=\overrightarrow{A{C}^{\text{'}}}$.     

B. $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$.

C. $\left|\overrightarrow{AB}\right|=\left|\overrightarrow{CD}\right|$.                      

D. $\overrightarrow{AB}=\overrightarrow{CD}$.

Hướng dẫn giải

Đáp án đúng là: D

Mệnh đề sai là: $\overrightarrow{AB}=\overrightarrow{CD}$, $\overrightarrow{AB}$ và $\overrightarrow{CD}$ là hai vectơ đối nhau.

Bài 3. Cho tứ diện đều ABCD có cạnh bằng a. Chứng minh rằng

a) $\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{BC}+\overrightarrow{DA}=\overrightarrow{0}$.

b) $\overrightarrow{AB}.\overrightarrow{AC}=\frac{a^2}{2}$.

c) $\overrightarrow{AB}.\overrightarrow{CD}=0$.

Hướng dẫn giải

Gọi M là trung điểm của BC và O là trọng tâm của tam giác BCD.

a) Ta có $\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{BC}+\overrightarrow{DA}=\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+\left(\overrightarrow{CD}+\overrightarrow{DA}\right)$$=\overrightarrow{AC}+\overrightarrow{CA}=\overrightarrow{0}$ .

b) Vì DABC đều nên $\left(\overrightarrow{AB},\overrightarrow{AC}\right)=60°$.

Có $\overrightarrow{AB}.\overrightarrow{AC}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|.\cos \left(\overrightarrow{AB},\overrightarrow{AC}\right)=a.a.\cos 60°=\frac{a^2}{2}$.

c) Vì ABCD là tứ diện đều, O là trọng tâm của tam giác BCD nên $AO\perp \left(BCD\right)$.

Suy ra $AO\perp CD$.

Lại có BO $\perp$ CD. Do đó CD $\perp$ (ABO). Suy ra CD $\perp$ AB hay $\overrightarrow{AB}.\overrightarrow{CD}=0$.

Bài 4. Cho hình chóp S.ABC có SA = SB = SC = AC = AB = a và $BC=a\sqrt{2}$. Tính góc $\left(\overrightarrow{SC},\overrightarrow{AB}\right)$.

Hướng dẫn giải

Từ giả thiết ta có DABC vuông tại A  nên $\overrightarrow{AB}.\overrightarrow{AC}=0$>và $\left(\overrightarrow{SA},\overrightarrow{AB}\right)=120°$.

Ta có $\cos \left(\overrightarrow{SC},\overrightarrow{AB}\right)=\frac{\overrightarrow{SC}.\overrightarrow{AB}}{\left|\overrightarrow{SC}\right|.\left|\overrightarrow{AB}\right|}$$=\frac{\left(\overrightarrow{SA}+\overrightarrow{AC}\right).\overrightarrow{AB}}{\left|\overrightarrow{SC}\right|.\left|\overrightarrow{AB}\right|}$$=\frac{\overrightarrow{SA}.\overrightarrow{AB}+\overrightarrow{AC}.\overrightarrow{AB}}{\left|\overrightarrow{SC}\right|.\left|\overrightarrow{AB}\right|}$$=\frac{\overrightarrow{SA}.\overrightarrow{AB}}{\left|\overrightarrow{SC}\right|.\left|\overrightarrow{AB}\right|}$$=\frac{\left|\overrightarrow{SA}\right|.\left|\overrightarrow{AB}\right|.\cos \left(\overrightarrow{SA},\overrightarrow{AB}\right)}{\left|\overrightarrow{SC}\right|.\left|\overrightarrow{AB}\right|}$$=\frac{a.a.\cos 120°}{a.a}$.

Suy ra $\left(\overrightarrow{SC},\overrightarrow{AB}\right)=120°$.

Bài 5. Theo định luật II Newton: gia tốc của một vật có cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực và tỉ lệ nghịch với khối lượng của vật: $\overrightarrow{F}=m\overrightarrow{a}$, trong đó $\overrightarrow{a}$  là vectơ gia tốc (m/s²), $\overrightarrow{F}$  có vectơ lực (N) tác dụng lên vật, m (kg) là khối lượng của vật. Một cầu thủ sút một quả bóng có khối lượng 0,6 kg với gia tốc 60 m/s² thì cần một lực đá có độ lớn là bao nhiêu?

Hướng dẫn giải

Ta có $\left|\overrightarrow{F}\right|=m\left|\overrightarrow{a}\right|=0,6.60=36N$ .

Vậy một lực có độ lớn là 36 N.

Học tốt Vectơ và các phép toán trong không gian

Các bài học để học tốt Vectơ và các phép toán trong không gian Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài 1: Vectơ và các phép toán trong không gian