Lý thuyết Toán lớp 12 Đường tiệm cận của đồ thị hàm số - Chân trời sáng tạo

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán lớp 12 Đường tiệm cận của đồ thị hàm số - Chân trời sáng tạo

Lý thuyết Đường tiệm cận của đồ thị hàm số

1. Đường tiệm cận đứng

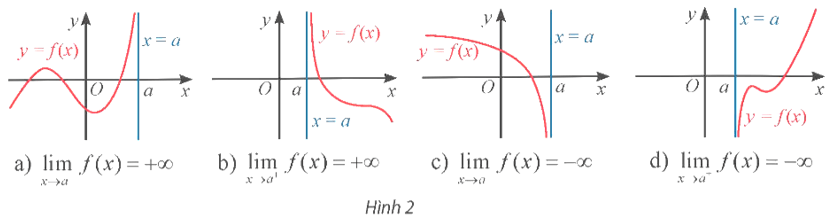
- Đường thẳng x = a được gọi là một đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau thỏa mãn:

$\underset{x\to a^{-}}{\lim }f\left(x\right)=+\infty ,\underset{x\to a^{+}}{\lim }f\left(x\right)=+\infty ,\underset{x\to a^{-}}{\lim }f\left(x\right)=-\infty ,\underset{x\to a^{+}}{\lim }f\left(x\right)=-\infty$

- Đường thẳng x = a là tiệm cận đứng của đồ thị hàm số y = f(x) được minh họa như Hình 2.

Ví dụ 1. Tìm tiệm cận đứng của đồ thị hàm số $y=\frac{2x+1}{x-1}$

Hướng dẫn giải

Tập xác định: D = ℝ\{1}.

Ta có $\underset{x\to 1^{+}}{\lim }\frac{2x+1}{x-1}=+\infty ;\underset{x\to 1^{-}}{\lim }\frac{2x+1}{x-1}=-\infty$

Do đó x = 1 là tiệm cận đứng của đồ thị hàm số.

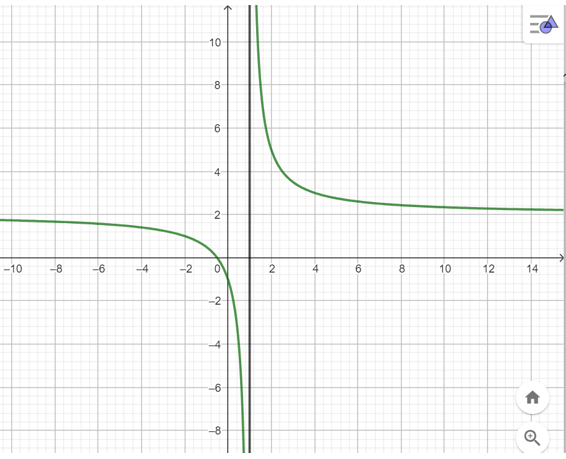
Chú ý: Đồ thị hàm số $y=\frac{2x+1}{x-1}$ cùng với tiệm cận đứng x = 1 được thể hiện trong hình sau:

2. Đường tiệm cận ngang

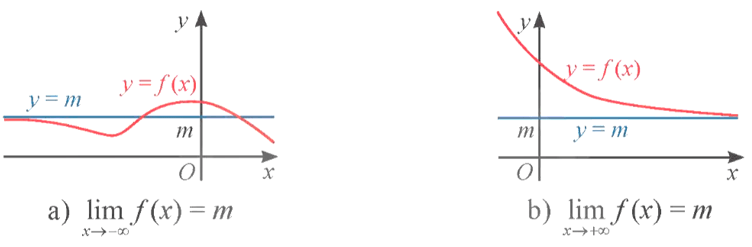
- Đường thẳng y = m được gọi là một đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu $\underset{x\to -\infty }{\lim }f\left(x\right)=m$ hoặc $\underset{x\to +\infty }{\lim }f\left(x\right)=m$

- Đường thẳng y = m là tiệm cận ngang của đồ thị hàm số y = f(x) được minh họa như hình bên dưới.

Ví dụ 2. Tìm tiệm cận ngang của đồ thị hàm số $y=\frac{x+1}{x-2}$

Hướng dẫn giải

Tập xác định: D = ℝ\{2}.

Có $\underset{x\to +\infty }{\lim }\frac{x+1}{x-2}=\underset{x\to +\infty }{\lim }\frac{1+\frac{1}{x}}{1-\frac{2}{x}}=1;\underset{x\to -\infty }{\lim }\frac{x+1}{x-2}=\underset{x\to -\infty }{\lim }\frac{1+\frac{1}{x}}{1-\frac{2}{x}}=1$

Do đó y = 1 là tiệm cận ngang của đồ thị hàm số.

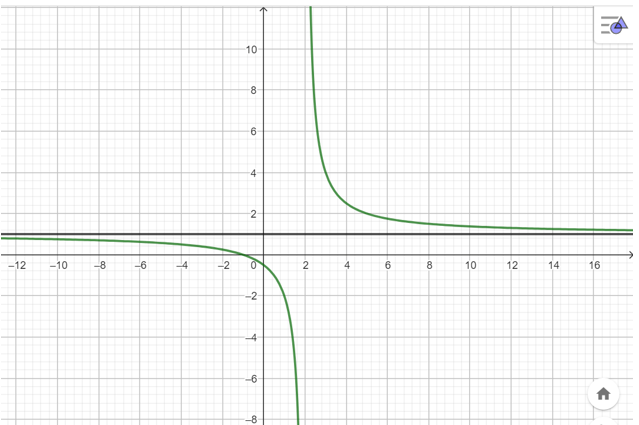
Chú ý: Đồ thị hàm số $y=\frac{x+1}{x-2}$ cùng với tiệm cận ngang y = 1 được thể hiện trong hình sau:

3. Đường tiệm cận xiên

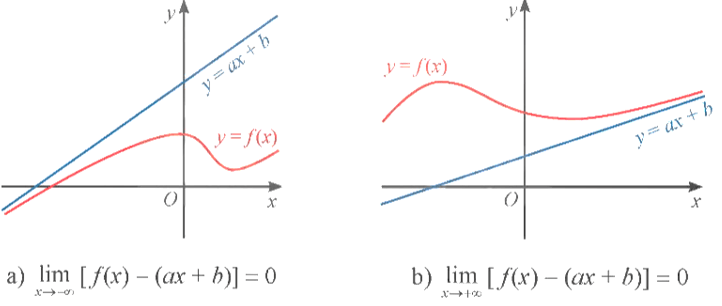
- Đường thẳng y = ax + b, a ≠ 0, được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu $\underset{x\to -\infty }{\lim }\left[f\left(x\right)-\left(ax+b\right)\right]=0$ hoặc $\underset{x\to +\infty }{\lim }\left[f\left(x\right)-\left(ax+b\right)\right]=0$

- Đường thẳng y = ax + b là tiệm cận xiên của đồ thị hàm số y = f(x) được minh họa như hình sau:

Ví dụ 3. Chứng minh rằng đường thẳng y = x là một tiệm cận xiên của đồ thị hàm số $y=f\left(x\right)=x+\frac{1}{x-1}$

Hướng dẫn giải

Tập xác định: D = ℝ\{1}.

Ta có $\underset{x\to -\infty }{\lim }\left[f\left(x\right)-x\right]=\underset{x\to -\infty }{\lim }\frac{1}{x-1}=0; \underset{x\to +\infty }{\lim }\left[f\left(x\right)-x\right]=\underset{x\to +\infty }{\lim }\frac{1}{x-1}=0$

Do đó y = x là tiệm cận xiên của đồ thị hàm số.

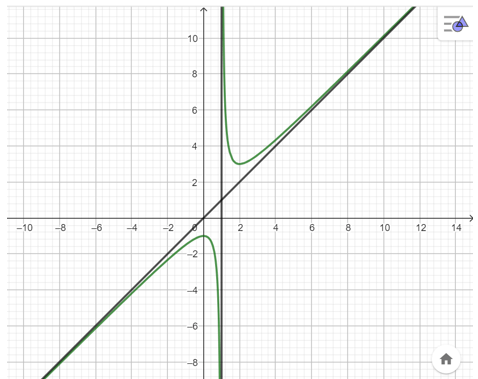
Chú ý: Đồ thị hàm số $y=f\left(x\right)=x+\frac{1}{x-1}$ cùng với tiệm cận đứng x = 1; tiệm cận xiên y = x được thể hiện trong hình vẽ sau:

Nhận xét:

a) Trong trường hợp tổng quát, có thể tìm các hệ số a, b trong phương trình của đường tiệm cận xiên y = ax + b theo công thức như sau:

$a=\underset{x\to +\infty }{\lim }\frac{f\left(x\right)}{x};b=\underset{x\to +\infty }{\lim }\left[f\left(x\right)-ax\right]$ hoặc $a=\underset{x\to -\infty }{\lim }\frac{f\left(x\right)}{x};b=\underset{x\to -\infty }{\lim }\left[f\left(x\right)-ax\right]$

b) Khi a = 0 thì đồ thị của hàm số có tiệm cận ngang là đường thẳng y = b.

Ví dụ 4. Tìm tiệm cận xiên của đồ thị hàm số $y=f\left(x\right)=\frac{x^2-3x+3}{x-2}$

Hướng dẫn giải

Tập xác định: D = ℝ\{2}.

Ta có <$a=\underset{x\to +\infty }{\lim }\frac{f\left(x\right)}{x}=\underset{x\to +\infty }{\lim }\frac{x^2-3x+3}{x^2-2x}=\underset{x\to +\infty }{\lim }\frac{1-\frac{3}{x}+\frac{3}{x^2}}{1-\frac{2}{x}}=1$

$b=\underset{x\to +\infty }{\lim }\left[f\left(x\right)-x\right]=\underset{x\to +\infty }{\lim }\left[\frac{x^2-3x+3}{x-2}-x\right]=\underset{x\to +\infty }{\lim }\frac{-x+3}{x-2}=-1$

Tương tự $a=\underset{x\to -\infty }{\lim }\frac{f\left(x\right)}{x}=1; b=\underset{x\to -\infty }{\lim }\left[f\left(x\right)-x\right]=-1$

Do đó y = x – 1 là tiệm cận xiên của đồ thị hàm số.

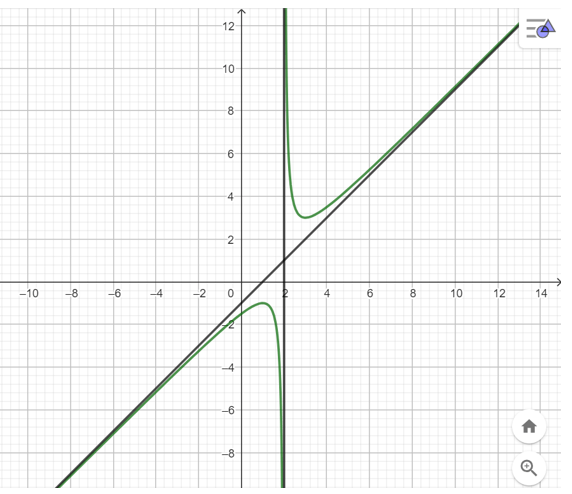
Chú ý: Đồ thị hàm số $y=f\left(x\right)=\frac{x^2-3x+3}{x-2}$ cùng với tiệm cận đứng x = 2 và tiệm cận xiên y = x – 1 được thể hiện trong hình vẽ sau:

Bài tập Đường tiệm cận của đồ thị hàm số

B. Bài tập tự luyện

Bài 1. Cho hàm số y = f(x) xác định trên ℝ\{1} và có $\underset{x\to -\infty }{\lim }f\left(x\right)=-2,\underset{x\to 1^{+}}{\lim }f\left(x\right)=+\infty ,\underset{x\to 1^{-}}{\lim }f\left(x\right)=+\infty ,\underset{x\to +\infty }{\lim }f\left(x\right)=2.$ Khẳng định nào sau đây đúng?

A. Đồ thị hàm số đã cho có đúng một tiệm cận ngang là đường thẳng y = 1.

B. Đồ thị hàm số đã cho có đúng hai tiệm cận ngang là các đường thẳng y = 2; y = −2.

C. Đồ thị hàm số đã cho có đúng hai tiệm cận đứng là các đường thẳng x = 2 và x = −2.

D. Đồ thị hàm số đã cho không có tiệm cận đứng.

Hướng dẫn giải

Đáp án đúng là: B

Có $\underset{x\to -\infty }{\lim }f\left(x\right)=-2,\underset{x\to 1^{+}}{\lim }f\left(x\right)=+\infty ,\underset{x\to 1^{-}}{\lim }f\left(x\right)=+\infty ,\underset{x\to +\infty }{\lim }f\left(x\right)=2$

Suy ra y = 2; y = −2 là các tiệm cận ngang của đồ thị hàm số và x = 1 là tiệm cận đứng của đồ thị hàm số.

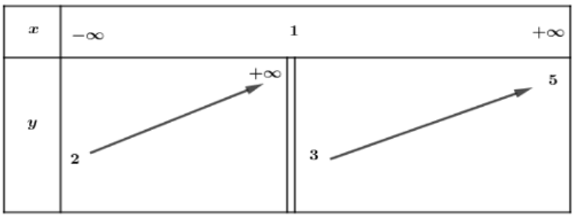
Bài 2. Cho hàm số y = f(x) có bảng biến thiên như sau

Tổng số đường tiệm cận ngang và đường tiệm cận đứng của đồ thị hàm số đã cho là

A. 3.

B. 2.

C. 4.

D. 1.

Hướng dẫn giải

Đáp án đúng là: A

Vì $\underset{x\to -\infty }{\lim }f\left(x\right)=2;\underset{x\to +\infty }{\lim }f\left(x\right)=5;\underset{x\to 1^{-}}{\lim }f\left(x\right)=+\infty$ nên đồ thị hàm số có hai tiệm cận ngang là y = 2; y = 5 và một tiệm cận đứng là x = 1.

Bài 3. Tìm tiệm cận đứng và tiệm cận ngang của đồ thị hàm số sau

a) $y=\frac{2x-1}{2x+4}$

b) $y=\frac{3x+2}{x-2}$

Hướng dẫn giải

a) Tập xác định: D = ℝ\{−2}.

Có $\underset{x\to {\left(-2\right)}^{-}}{\lim }\frac{2x-1}{2x+4}=+\infty ;\underset{x\to {\left(-2\right)}^{+}}{\lim }\frac{2x-1}{2x+4}=-\infty$

Do đó x = −2 là tiệm cận đứng của đồ thị hàm số.

Có $\underset{x\to +\infty }{\lim }\frac{2x-1}{2x+4}=\underset{x\to +\infty }{\lim }\frac{2-\frac{1}{x}}{2+\frac{4}{x}}=1$; $\underset{x\to -\infty }{\lim }\frac{2x-1}{2x+4}=\underset{x\to -\infty }{\lim }\frac{2-\frac{1}{x}}{2+\frac{4}{x}}=1$

Do đó y = 1 là tiệm cận ngang của đồ thị hàm số.

b) Tập xác định: D = ℝ\{2}.

Có $\underset{x\to 2^{+}}{\lim }\frac{3x+2}{x-2}=+\infty ;\underset{x\to 2^{-}}{\lim }\frac{3x+2}{x-2}=-\infty$

Do đó x = 2 là tiệm cận đứng của đồ thị hàm số.

Có $\underset{x\to +\infty }{\lim }\frac{3x+2}{x-2}=3;\underset{x\to -\infty }{\lim }\frac{3x+2}{x-2}=3$

Do đó y = 3 là tiệm cận ngang của đồ thị hàm số.

Bài 4. Tìm tiệm cận đứng và tiệm cận xiên của đồ thị hàm số sau

a) $y=f\left(x\right)=\frac{x^2-x-1}{x-1}$

b) $y=f\left(x\right)=\frac{2x^2+3x+2}{x+1}$

Hướng dẫn giải

a) Tập xác định: D = ℝ\{1}.

Có $\underset{x\to 1^{+}}{\lim }\frac{x^2-x-1}{x-1}=-\infty ;\underset{x\to 1^{-}}{\lim }\frac{x^2-x-1}{x-1}=+\infty$

Do đó x = 1 là tiệm cận đứng của đồ thị hàm số.

$b=\underset{x\to +\infty }{\lim }\left[f\left(x\right)-x\right]=\underset{x\to +\infty }{\lim }\left[\frac{x^2-x-1}{x-1}-x\right]=\underset{x\to +\infty }{\lim }\left(-\frac{1}{x-1}\right)=0$

Tương tự $a=\underset{x\to -\infty }{\lim }\frac{f\left(x\right)}{x}=1$; $b=\underset{x\to -\infty }{\lim }\left[f\left(x\right)-x\right]=0$

Do đó y = x là tiệm cận xiên của đồ thị hàm số.

b) Tập xác định: D = ℝ\{−1}.

Có $\underset{x\to {\left(-1\right)}^{-}}{\lim }\frac{2x^2+3x+2}{x+1}=-\infty ;\underset{x\to {\left(-1\right)}^{+}}{\lim }\frac{2x^2+3x+2}{x+1}=+\infty$

Do đó x = −1 là tiệm cận đứng của đồ thị hàm số.

Có $a=\underset{x\to +\infty }{\lim }\frac{f\left(x\right)}{x}=\underset{x\to +\infty }{\lim }\frac{2x^2+3x+2}{x^2+x}=2$

$b=\underset{x\to +\infty }{\lim }\left[f\left(x\right)-2x\right]=\underset{x\to +\infty }{\lim }\left[\frac{2x^2+3x+2}{x+1}-2x\right]=\underset{x\to +\infty }{\lim }\frac{x+2}{x-1}=1$

Tương tự $a=\underset{x\to -\infty }{\lim }\frac{f\left(x\right)}{x}=2$; $b=\underset{x\to -\infty }{\lim }\left[f\left(x\right)-2x\right]=1$

Do đó y = 2x + 1 là tiệm cận xiên của đồ thị hàm số.

Bài 5. Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được tính theo công thức $c\left(t\right)=\frac{t}{t^2+1}$ (mg/l). Tìm các đường tiệm cận của đồ thị hàm số y = c(t).

Hướng dẫn giải

Tập xác định: D = (0; +∞).

$\underset{t\to +\infty }{\lim }c\left(t\right)=\underset{t\to +\infty }{\lim }\frac{t}{t^2+1}=0$

Do đó y = 0 là tiệm cận ngang của đồ thị hàm số.

Đồ thị hàm số không có tiệm cận đứng.

Học tốt Đường tiệm cận của đồ thị hàm số

Các bài học để học tốt Đường tiệm cận của đồ thị hàm số Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số