Lý thuyết Toán lớp 12 Xác suất có điều kiện - Chân trời sáng tạo

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 12 Bài 1: Xác suất có điều kiện sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 12 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12.

Lý thuyết Toán lớp 12 Xác suất có điều kiện - Chân trời sáng tạo

Lý thuyết Xác suất có điều kiện

1. Xác suất có điều kiện

Cho hai biến cố A và B. Xác suất của biến cố B khi biến cố A đã xảy ra được gọi là xác suất của B với điều kiện A, kí hiệu P(B | A).

Ví dụ 1. Câu lạc bộ nghệ thuật của nhà trường gồm 50 thành viên, mỗi thành viên đều biết ít nhất một trong hai hoạt động là hát hoặc nhảy. Biết rằng có 30 thành viên biết hát và 35 thành viên biết nhảy. Chọn ngẫu nhiên một thành viên của câu lạc bộ. Tính xác suất thành viên được chọn biết hát, biết rằng thành viên đó biết nhảy.

Hướng dẫn giải

Gọi A là biến cố “Thành viên được chọn biết nhảy” và B là biến cố “Thành viên được chọn biết hát”.

Số thành viên của câu lạc bộ biết cả hát và nhảy là 30 + 35 – 50 = 15.

Do đó, trong số 35 thành viên biết nhảy, có đúng 15 thành viên biết hát.

Vậy nên xác suất thành viên được chọn biết hát, biết rằng thành viên đó biết nhảy là

                                      P(B | A) = $\frac{15}{35}=\frac{3}{7}$.

2. Công thức tính xác suất có điều kiện

Cho A và B là hai biến cố, trong đó P(B) > 0. Khi đó

$P\left(A|B\right)=\frac{P\left(A\cap B\right)}{P\left(B\right)}$.

Chú ý:

a) Ta cũng kí hiệu biến cố giao của hai biến cố A và B là AB.

b) Trong thực tế, người ta thường dùng tỉ lệ phần trăm để mô tả xác suất. Chẳng hạn, phát biểu “Khả năng xảy ra một sự kiện là 20%” cũng có nghĩa là “Xác suất xảy ra sự kiện đó là 0,2”, phát biểu “Tỉ lệ phế phẩm của một lô hàng là 5%” cũng có nghĩa là “Nếu chọn ra ngẫu nhiên 1 sản phẩm từ lô hàng, xác suất sản phẩm đó là phế phẩm là 0,05”.

Ví dụ 2. Một công ty bảo hiểm nhận thấy có 70% số người mua bảo hiểm ô tô là đàn ông và có 35% số người mua bảo hiểm ô tô là đàn ông trên 50 tuổi.

a) Biết rằng người mua bảo hiểm ô tô là đàn ông, tính xác suất người đó trên 50 tuổi.

b) Tính tỉ lệ người trên 50 tuổi trong số những người đàn ông mua bảo hiểm ô tô.

Hướng dẫn giải

a) Gọi A là biến cố “Người mua bảo hiểm ô tô là đàn ông”, B là biến cố “Người mua bảo hiểm ô tô trên 50 tuổi”. Ta cần tính P(B | A).

Do có 70% số người mua bảo hiểm ô tô là đàn ông nên P(A) = 0,70.

Do có 35% số người mua bảo hiểm ô tô là đàn ông trên 50 tuổi nên P(AB) = 0,35.

Vậy P(B | A) = $\frac{P\left(AB\right)}{P\left(A\right)}=\frac{0,35}{0,70}=0,5$.

b) Trong số những người đàn ông mua bảo hiểm ô tô thì có 50% người trên 50 tuổi.

Chú ý:

a) Từ công thức xác suất có điều kiện, với P(B) > 0, ta có P(AB) = P(B) P(A | B).

b) Trong trường hợp tổng quát, người ta chứng minh được rằng với A, B là hai biến cố bất kì thì

P(AB) = P(B) P(A | B).

Công thức trên được gọi là công thức nhân xác suất cho hai biến cố.

Ví dụ 3. Cho hai biến cố A và B có P(A) = 0,2; P(B) = 0,6 và P(A | B) = 0,3.

Tính P( $\overline{A}$B) và P( $\overline{A}$ | B).

Hướng dẫn giải

Theo công thức nhân xác suất, ta có P(AB) = P(B) P(A | B) = 0,6 ∙ 0,3 = 0,18.

Vì B và AB là hai biến cố xung khắc và $\overline{A}$B $\cup$ AB = B nên theo tính chất của xác suất, ta có P( $\overline{A}$B) = P(B) – P(AB) = 0,6 – 0,18 = 0,42.

Theo công thức tính xác suất có điều kiện, ta có P( $\overline{A}$ | B) $=\frac{P\left(\overline{A}B\right)}{P\left(B\right)}=\frac{0,42}{0,6}=0,7$.

Chú ý:

a) Với mọi biến cố A và B, trong đó P(B) > 0, ta có

P( $\overline{A}$ | B) = 1 – P(A | B).

b) Với A và B là hai biến cố độc lập, trong đó 0 < P(B) < 1, người ta chứng minh được rằng

P(A | B) = P(A | $\overline{B}$ ) = P(A).

Từ đẳng thức trên, ta thấy khi A và B độc lập thì việc biến cố B xảy ra hay không xảy ra không làm ảnh hưởng đến xác suất của biến cố A.

3. Sơ đồ hình cây

Nhận xét: Trên sơ đồ hình cây:

+ Xác suất của các nhánh trong sơ đồ hình cây từ đỉnh thứ hai là xác suất có điều kiện.  

+ Xác suất xảy ra của mỗi kết quả bằng tích các xác suất trên các nhánh của cây đi đến kết quả đó.

Ví dụ 4. Hộp thứ nhất có 6 quả bóng bàn màu trắng và 4 quả bóng bàn màu vàng. Hộp thứ hai có 3 quả bóng bàn màu trắng và 5 quả bóng bàn màu vàng. Các quả bóng bàn có cùng kích thước và khối lượng. Lấy ngẫu nhiên một quả bóng bàn từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên 1 quả bóng bàn từ hộp thứ hai.

Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:

A: “Quả bóng bàn lấy ra từ hộp thứ nhất có màu trắng và quả bóng bàn lấy ra từ hộp thứ hai có màu vàng”;

B: “Hai quả bóng bàn lấy ra có cùng màu”.

Hướng dẫn giải

Gọi M là biến cố “Quả bóng bàn lấy ra từ hộp thứ nhất có màu trắng” và N là biến cố “Quả bóng bàn lấy ra từ hộp thứ hai có màu vàng”.

Từ giả thiết, ta có: P(M) = $\frac{6}{10}$; P(N | M) = $\frac{5}{9}$; P(N | $\overline{M}$) = $\frac{6}{9}$.

Do đó, P($\overline{M}$) = 1 – P(M) = $\frac{4}{10}$; P( $\overline{N}$|M) = 1 – P(N | M) = $\frac{4}{9}$;

P($\overline{N}$|$\overline{M}$) = 1 – P(N | $\overline{M}$ ) = $\frac{3}{9}$.

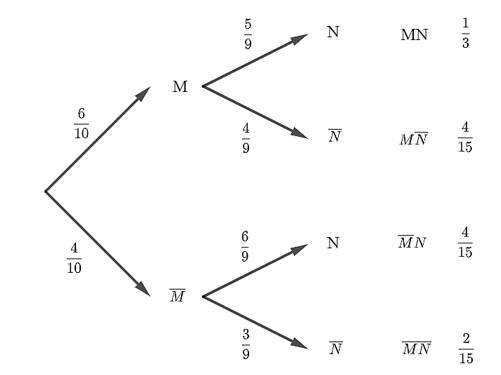
Ta có sơ đồ hình cây như sau:

Do A = MN nên P(A) = P(MN) = $\frac{1}{3}$.

Do B = M$\overline{N}$ $\cup$ $\overline{M}$N nên P(B) = P(M$\overline{N}$) + P($\overline{M}$N) = $\frac{4}{15}+\frac{4}{15}=\frac{8}{15}$.

Bài tập Xác suất có điều kiện

Bài 1. Cho hai biến cố A và B có P(A) = 0,5; P(B) = 0,7; P(AB) = 0,4. Tính P(A | B) được kết quả là

A. $\frac{4}{7}$.

B. $\frac{1}{5}$.

C. $\frac{4}{5}.$

D.$\frac{1}{7}.$

Hướng dẫn giải

Đáp án đúng là: A

Ta có: $P\left(A|B\right)=\frac{P\left(AB\right)}{P\left(B\right)}=\frac{0,4}{0,7}=\frac{4}{7}$.

Bài 2. Cho hai biến cố A và B có P(A) = 0,5; P(B) = 0,7; P(AB) = 0,4. Xác suất của biến cố B không xảy ra với điều kiện biến cố A xảy ra là

A. 0,8.

B. $\frac{3}{7}.$

C. 0,2.

D. $\frac{5}{6}.$

Hướng dẫn giải

Đáp án đúng là: C

Xác suất của biến cố B không xảy ra với điều kiện biến cố A xảy ra chính là xác suất có điều kiện P($\overline{B}$| A).

Ta có P(B | A) = $\frac{P\left(BA\right)}{P\left(A\right)}=\frac{P\left(AB\right)}{P\left(A\right)}=\frac{0,4}{0,5}=\frac{4}{5}$.

Khi đó, P( $\overline{B}$| A) = 1 – P(B | A) = $1-\frac{4}{5}=\frac{1}{5}$= 0,2.

Bài 3. Một bình đựng 13 viên bi xanh và 17 viên bi đỏ. Lần lượt lấy ngẫu nhiên ra 2 viên bi, mỗi lần lấy 1 viên bi không hoàn lại. Tính xác suất để viên bi thứ hai màu xanh nếu biết viên bi thứ nhất màu đỏ.

Hướng dẫn giải

Gọi biến cố A: “Viên bi thứ nhất là màu đỏ”.

Biến cố B: “Viên bi thứ hai là màu xanh”.

Ta cần tính P(B | A).

Từ giả thiết, ta có $P\left(A\right)=\frac{17}{30}$; $P\left(AB\right)=\frac{17}{30}\cdot \frac{13}{29}=\frac{221}{870}$.

Do đó $P\left(B|A\right)=\frac{P\left(AB\right)}{P\left(A\right)}=\frac{221}{870}:\frac{17}{30}=\frac{13}{29}$.

Vậy xác suất để viên bi thứ hai màu xanh nếu biết viên bi thứ nhất màu đỏ bằng $\frac{13}{29}$.

Bài 4. Mỗi bạn học sinh trong lớp của Linh lựa chọn tham gia một trong hai câu lạc bộ thể thao là bóng đá và bóng chuyền. Xác suất chọn bóng đá của mỗi bạn học sinh nữ là 0,4 và của mỗi bạn học sinh nam là 0,8. Lớp của Linh có 15 bạn nữ và 25 bạn nam. Chọn ra ngẫu nhiên một bạn trong lớp.

Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:

A: “Bạn được chọn là nam và tham gia câu lạc bộ bóng chuyền”;

B: “Bạn được chọn là nữ và tham gia câu lạc bộ bóng đá”.

Hướng dẫn giải

Ta có sơ đồ hình cây của bài toán trên như sau:

Theo sơ đồ hình cây, ta có P(A) = 0,125 và P(B) = 0,15.

Bài 5. Một doanh nghiệp trước khi xuất khẩu áo sơ mi trong lô hàng M phải qua hai lần kiểm tra chất lượng sản phẩm, nếu cả hai lần đều đạt thì chiếc áo trong lô hàng đó mới đủ tiêu chuẩn xuất khẩu. Biết rằng bình quân 97% sản phẩm làm ra qua được lần kiểm tra thứ nhất và 96% sản phẩm qua được lần kiểm tra thứ nhất sẽ tiếp tục qua được lần kiểm tra thứ hai. Chọn ra ngẫu nhiên một chiếc áo sơ mi trong lô hàng M. Tính xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu.

Hướng dẫn giải

Gọi A là biến cố “Chiếc áo sơ mi qua được lần kiểm tra thứ nhất”; B là biến cố “Chiếc áo sơ mi qua được lần kiểm tra thứ hai”; C là biến cố “Chiếc áo sơ mi đủ tiêu chuẩn”.

Khi đó, xác suất để chiếc áo sơ mi qua được lần kiểm tra thứ hai, biết rằng đã qua lần kiểm tra thứ nhất, là xác suất có điều kiện P(B | A) và P(C) = P(BA).

Ta có: P(B | A) = 0,96; P(A) = 0,97.

Suy ra P(C) = P(BA) = P(A) ∙ P(B | A) = 0,97 ∙ 0,96 = 0,9312.

Vậy xác suất để một chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu là 0,9312.

Học tốt Xác suất có điều kiện

Các bài học để học tốt Xác suất có điều kiện Toán lớp 12 hay khác:

• Giải sgk Toán 12 Bài 1: Xác suất có điều kiện