Tóm tắt lý thuyết Toán lớp 6 Chương 6: Phân số | Lý thuyết Toán lớp 6 chi tiết Kết nối tri thức
Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán lớp 6 Chương 6: Phân số hay nhất, chi tiết sách Kết nối tri thức với cuộc sống sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 6.
Toán lớp 6 Chương 6: Phân số - Lý thuyết chi tiết
Lý thuyết Toán 6 Bài 23: Mở rộng phân số. Phân số bằng nhau
I. Lý thuyết
1. Mở rộng khái niệm về phân số
– Định nghĩa về phân số: Với a, b ∈ ℤ, b ≠ 0 , ta gọi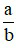 
là một phân số, trong đó a là tử số (tử), b là mẫu số (mẫu) của phân số.
Ví dụ 1:
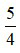là một phân số với tử số là 5 và mẫu số là 4 đọc là năm phần tư.
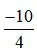là một phân số với tử số là –10 và mẫu số là 4 đọc là âm mười phần tư.
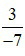là một phân số với tử số là 3 và mẫu số là –7 đọc là ba phần âm bảy.
Chú ý: Mọi số nguyên đều có thể viết dưới dạng phân số.
Ví dụ 2:
Số 3 có thể viết dưới dạng phân số là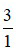 
.
Số –8 có thể viết dưới dạng phân số là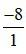 
.
2. Hai phân số bằng nhau
Hai phân số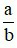 
và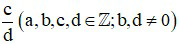 
được gọi là bằng nhau nếu a.d = b.c. Khi đó ta viết là 
.
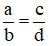Ví dụ 3: Hai phân số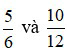 
bằng nhau vì 5.12 = 60 và 6.10 = 60.
3. Tính chất cơ bản của phân số
– Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.
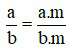với a, b, m ∈ ℤ; b≠0; m≠0.
– Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.
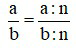với n là ước chung của a và b; a, b, m ∈ ℤ; b≠0 .
Ví dụ 4:
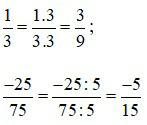
Lý thuyết Toán 6 Bài 24: So sánh phân số. Hỗn số dương
I. Lý thuyết
1. Quy đồng mẫu nhiều phân số
Để quy đồng hai hay nhiều phân số ta làm như sau:
Bước 1: Tìm một bội chung (thường là BCNN) của các mẫu để làm mẫu chung.
Bước 2: Tìm thừa số phụ của mỗi mẫu bằng cách chia mẫu chung cho từng mẫu.
Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
Ví dụ 1: Để quy đồng ba phân số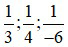 
ta làm như sau:
+ Đưa về các phân số có mẫu dương: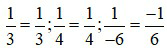 
.
+ Tìm mẫu chung: BCNN (3; 4; 6) = 12
+ Thừa số phụ:
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
Ta có:
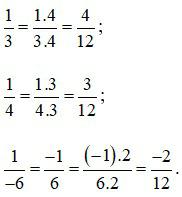
2. So sánh hai phân số
a) So sánh hai phân số cùng mẫu
– Trong hai phân số cùng một mẫu dương, phân số nào có tử lớn hơn thì phân số đó lớn hơn.
Ví dụ 2: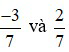 
là hai phân số có cùng mẫu số dương.
Vì –3 < 2 nên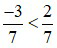 
.
b) So sánh hai phân số không cùng mẫu
– Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử số với nhau: phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
Ví dụ 3: So sánh hai phân số sau: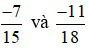 
.
BCNN (15; 18) = 90
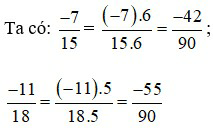
Vì –42 > –55 nên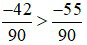 
do đó,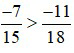
3. Hỗn số dương
– Khái niệm hỗn số dương: Với a, b, c là những số nguyên dương, ta gọi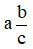 
là một hỗn số dương với a là phần nguyên và 
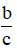là phần phân số.
Ví dụ 4:
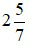là một hỗn số dương với phần nguyên là 2 và phần phân số là 
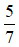. Khi đó ta đọc 
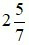là hai năm phần bảy.
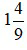là một hỗn số dương với phần nguyên là 1 và phần phân số là 
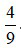. Khi đó ta đọc
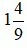là một bốn phần chín.
– Muốn đổi từ hỗn số sang phân số ta làm như sau:
Bước 1: Giữ nguyên phần mẫu số.
Bước 2: Phần tử số mới sẽ bằng phần mẫu số nhân với phần nguyên và cộng với phần tử số ban đầu.
Ví dụ 5: Đổi hỗn số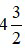 
sang phân số:
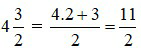
– Muốn đổi từ phân số sang hỗn số (điều kiện tử số của phân số phải lớn hơn mẫu số) ta làm như sau:
Bước 1: Giữ nguyên phần mẫu số và mẫu số này sẽ là mẫu số trong phần hỗn số mới.
Bước 2: Lấy phần tử số chia cho mẫu số, phần thương sẽ là phần nguyên trong hỗn số mới và phần dư là tử số mới của hỗn số.
Ví dụ 6: Đổi phân số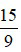 
sang hỗn số
Ta có 15 chia 9 được thương là 1 và dư 6 do đó:
....................................
....................................
....................................
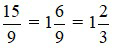
