Bài 9.28 trang 103 Toán 8 Tập 2 | Kết nối tri thức Giải Toán 8

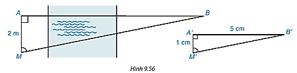
Một người ở vị trí điểm A muốn đo khoảng cách đến điểm B ở bên kia sông mà không thể qua sông được. Sử dụng giác kế, người đó xác định được một điểm M trên bờ sông sao cho AM = 2 m, AM vuông góc với AB và đo được số đo góc AMB. Tiếp theo, người đó vẽ trên giấy tam giác A'M'B' vuông tại A' có A'M' = 1 cm, và đo được A'B' = 5 cm (H.9.56). Hỏi khoảng cách từ A đến B là bao nhiêu mét?

Giải Toán 8 Bài 36: Các trường hợp đồng dạng của hai tam giác vuông - Kết nối tri thức

Bài 9.28 trang 103 Toán 8 Tập 2: Một người ở vị trí điểm A muốn đo khoảng cách đến điểm B ở bên kia sông mà không thể qua sông được. Sử dụng giác kế, người đó xác định được một điểm M trên bờ sông sao cho AM = 2 m, AM vuông góc với AB và đo được số đo góc AMB. Tiếp theo, người đó vẽ trên giấy tam giác A'M'B' vuông tại A' có A'M' = 1 cm, $\widehat{A\text{'}M\text{'}B\text{'}}=\widehat{AMB}$ và đo được A'B' = 5 cm (H.9.56). Hỏi khoảng cách từ A đến B là bao nhiêu mét?

Lời giải:

Ta có A'M' = 1 cm = 0,01 m; A'B' = 5 cm = 0,05 m.

Xét ΔA′M′B′ (vuông tại A') và ΔAMB (vuông tại A) có $\widehat{A\text{'}M\text{'}B\text{'}}=\widehat{AMB}$ (giả thiết).

Do đó, ΔA′M′B′ ∽ ΔAMB.

Suy ra $\frac{A\text{'}M\text{'}}{AM}=\frac{A\text{'}B\text{'}}{AB}$  hay $\frac{\mathrm{0,01}}{2}=\frac{\mathrm{0,05}}{AB}$ . Suy ra AB $=\frac{\mathrm{0,05}\cdot 2}{\mathrm{0,01}}$  = 10 (m).

Vậy khoảng cách từ A đến B là 10 m.

Lời giải bài tập Toán 8 Bài 36: Các trường hợp đồng dạng của hai tam giác vuông hay, chi tiết khác:

• Mở đầu trang 98 Toán 8 Tập 2: Nam và Việt muốn đo chiều cao của cột cờ ở sân trường mà hai bạn không trèo lên ....

• Câu hỏi trang 98 Toán 8 Tập 2: Hãy chỉ ra hai cặp tam giác vuông đồng dạng trong Hình 9.46 ....

• Luyện tập 1 trang 99 Toán 8 Tập 2: Trở lại tình huống mở đầu, ta thấy chiếc cột cùng với bóng của nó tạo thành hai cạnh góc ....

• Thử thách nhỏ trang 100 Toán 8 Tập 2: Một người đo chiều cao của một cái cây bằng cách chôn một chiếc cọc ....

• HĐ1 trang 100 Toán 8 Tập 2: Các tam giác vuông AHB và A'H'B' trong Hình 9.50 mô ....

• Câu hỏi trang 101 Toán 8 Tập 2: Hãy chỉ ra các cặp tam giác vuông đồng dạng với nhau trong ....

• Luyện tập 2 trang 102 Toán 8 Tập 2: Một ngôi nhà với hai mái lệch AB, CD được thiết kế như Hình 9.54 sao cho ....

• Vận dụng trang 102 Toán 8 Tập 2: Bác Minh muốn thay chiếc ti vi có chiều ngang của màn hình là 72 cm ....

• Bài 9.23 trang 102 Toán 8 Tập 2: Điều kiện nào dưới đây chứng tỏ rằng hai tam giác vuông đồng dạng? ....

• Bài 9.24 trang 103 Toán 8 Tập 2: Cặp tam giác vuông nào đồng dạng với nhau trong Hình 9.55? ....

• Bài 9.25 trang 103 Toán 8 Tập 2: Cho góc nhọn xOy, các điểm A, N nằm trên tia Ox, các điểm B, M nằm trên tia Oy ....

• Bài 9.26 trang 103 Toán 8 Tập 2: Cho hai hình chữ nhật ABCD và A'B'C'D' thỏa mãn AC ....

• Bài 9.27 trang 103 Toán 8 Tập 2: Cho ΔA'B'C' ∽ ΔABC theo tỉ số k. Gọi A'H' và AH lần lượt là các đường cao ....