Giải Toán 9 trang 96 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 9 trang 96 Tập 1 trong Bài 3: Góc ở tâm, góc nội tiếp Toán lớp 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 96.

Giải Toán 9 trang 96 Tập 1 Chân trời sáng tạo

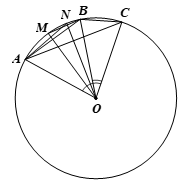
Thực hành 5 trang 96 Toán 9 Tập 1: Cho ba điểm A, B, C nằm trên đường tròn (O) sao cho $\widehat{AOB}=50°,$ $\widehat{BOC}=30°,$ điểm B thuộc cung nhỏ AC. Gọi M, N lần lượt là hai điểm trên hai cung nhỏ $\stackrel{⏜}{AB},\stackrel{⏜}{AC}$ và chia mỗi cung đó thành hai cung bằng nhau. Tìm số đo các góc sau:

a) $\widehat{BCA},\widehat{BAC};$

b) $\widehat{MBA},\widehat{BAN}.$

Lời giải:

a) Xét đường tròn (O), ta có:

⦁ $\widehat{BCA}$ và $\widehat{BOA}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung AB nên $\widehat{BCA}=\frac{1}{2}\widehat{BOA}=\frac{1}{2}\cdot 50°=25°.$

⦁ $\widehat{BCA}$ và $\widehat{BOC}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung BC nên $\widehat{BAC}=\frac{1}{2}\widehat{BOC}=\frac{1}{2}\cdot 30°=15°.$

b) Xét đường tròn (O), ta có điểm B thuộc cung nhỏ AC nên:

$sđ\stackrel{⏜}{AC}=sđ\stackrel{⏜}{AB}+sđ\stackrel{⏜}{BC}=\widehat{AOB}+\widehat{BOC}=50°+30°=80°.$

Vì M, N lần lượt chia $\stackrel{⏜}{AB},\stackrel{⏜}{AC}$ thành hai cung bằng nhau nên:

⦁ $sđ\stackrel{⏜}{AM}=\frac{1}{2}sđ\stackrel{⏜}{AB}=\frac{1}{2}\widehat{AOB}=\frac{1}{2}\cdot 50°=25°;$

⦁ $sđ\stackrel{⏜}{NC}=\frac{1}{2}sđ\stackrel{⏜}{AC}=\frac{1}{2}\widehat{AOC}=\frac{1}{2}\cdot 80°=40°.$

Ta có: điểm B thuộc cung nhỏ CN nên: $sđ\stackrel{⏜}{NC}=sđ\stackrel{⏜}{BN}+sđ\stackrel{⏜}{BC}$

Suy ra $sđ\stackrel{⏜}{BN}=sđ\stackrel{⏜}{NC}-sđ\stackrel{⏜}{BC}=40°-30°=10°.$

Ta có:

⦁ $\widehat{MBA}$ là góc nội tiếp chắn cung AM nên $\widehat{MBA}=\frac{1}{2}sđ\stackrel{⏜}{AM}=\frac{1}{2}\cdot 25°=\mathrm{12,5}°;$

⦁ $\widehat{BAN}$ là góc nội tiếp chắn cung BN nên $\widehat{BAN}=\frac{1}{2}sđ\stackrel{⏜}{BN}=\frac{1}{2}\cdot 10°=5°.$

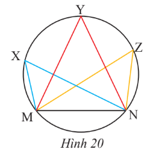
Vận dụng 5 trang 96 Toán 9 Tập 1: Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn MN (Hình 20). Nếu bóng được đặt ở điểm X thì $\widehat{MXN}$ gọi là góc sút từ vị trí X. Hãy so sánh các góc sút $\widehat{MXN}, \widehat{MYN}, \widehat{MZN}.$

Lời giải:

Xét đường tròn chứa cung MN, ta có $\widehat{MXN}, \widehat{MYN}, \widehat{MZN}$ là các góc nội tiếp chắn cung MN nên $\widehat{MXN}=\widehat{MYN}=\widehat{MZN}.$

Vậy các góc sút $\widehat{MXN}, \widehat{MYN}, \widehat{MZN}$ bằng nhau.

Lời giải bài tập Toán 9 Bài 3: Góc ở tâm, góc nội tiếp hay khác:

• Giải Toán 9 trang 90

• Giải Toán 9 trang 91

• Giải Toán 9 trang 92

• Giải Toán 9 trang 93

• Giải Toán 9 trang 97