Các dạng bài tập Hàm số lượng giác chọn lọc, có lời giải - Toán lớp 11

---

Các dạng bài tập Hàm số lượng giác chọn lọc, có lời giải

Với Các dạng bài tập Hàm số lượng giác chọn lọc, có lời giải Toán lớp 11 tổng hợp các dạng bài tập, trên 100 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Hàm số lượng giác từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

• Dạng 1: Tập xác định, tập giá trị của hàm số lượng giác Xem chi tiết
• Trắc nghiệm tập xác định, tập giá trị của hàm số lượng giác Xem chi tiết
• Dạng 2: Tính chẵn, lẻ và chu kì của hàm số lượng giác Xem chi tiết
• Trắc nghiệm tính chẵn, lẻ và chu kì của hàm số lượng giác Xem chi tiết
• Tìm tập xác định của hàm số lượng giác Xem chi tiết
• Tính đơn điệu của hàm số lượng giác Xem chi tiết
• Xác định tính chẵn, lẻ của hàm số lượng giác Xem chi tiết
• Tính chu kì tuần hoàn của hàm số lượng giác Xem chi tiết
• Giá trị lớn nhất, nhỏ nhất của hàm số lượng giác Xem chi tiết
• 60 bài tập trắc nghiệm hàm số lượng giác có đáp án Xem chi tiết

Cách tìm Tập xác định, tập giá trị của hàm số lượng giác

A. Phương pháp giải & Ví dụ

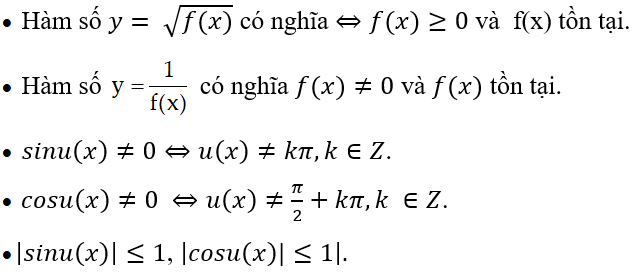
Ví dụ minh họa

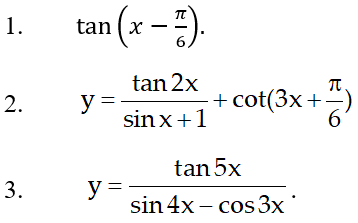
Đáp án và hướng dẫn giải

1.

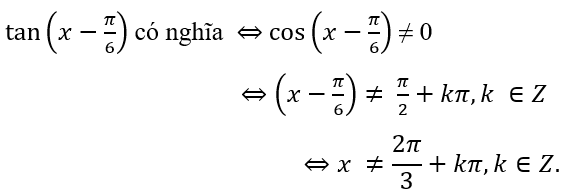
Vậy tập xác định của hàm số trên là

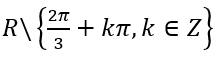
2.

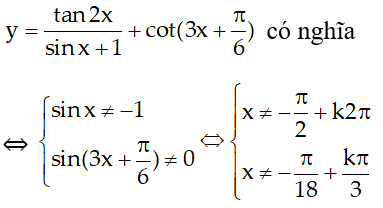
Vậy tập xác định của hàm số trên là

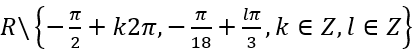
3.

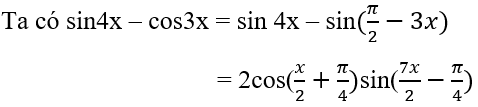
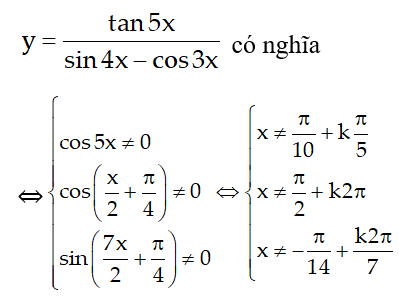
Vậy tập xác định của hàm số trên là

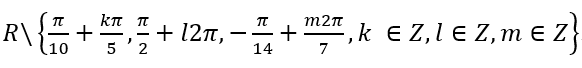
Cách xét Tính chẵn, lẻ và chu kì của hàm số lượng giác

A. Phương pháp giải & Ví dụ

a. Tính tuần hoàn và chu kì:

Định nghĩa: Hàm số y = f(x) có tập xác định được gọi là hàm số tuần hoàn, nếu tồn tại một số T≠0 sao cho với mọi x ∈ D ta có:

        ♦ (x- T) ∈ D và (x + T) ∈ D

        ♦ f (x + T) = f(x).

Số dương T nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó. Người ta chứng minh được rằng hàm số y = sinx tuần hoàn với chu kì T = 2 π ; hàm số y = cosx tuần hoàn với chu kì T = 2 π; hàm số y = tanx tuần hoàn với chu kì T = π; hàm số y = cotx tuần hoàn với chu kì T = π

Chú ý:

    Hàm số y = sin(ax + b) tuần hoàn với chu kì T =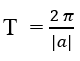

    Hàm số y = cos(ax + b) tuần hoàn với chu kì T =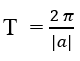

    Hàm số y = tan(ax + b) tuần hoàn với chu kì T =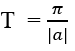

    Hàm số y = cot(ax + b) tuần hoàn với chu kì T =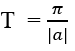

    Hàm số y = f₁(x) tuần hoàn với chu kì T₁ và hàm số y = f₂(x) tuần hoàn với chu kì T₂ thì hàm số y = f₁(x) ± f₂(x) tuần hoàn với chu kì T₀ là bội chung nhỏ nhất của T₁ và T₂ .

b. Hàm số chẵn, lẻ:

Định nghĩa:

    Hàm số y = f(x) có tập xác định là D được gọi là hàm số chẵn nếu:

        ♦ x ∈ D và – x ∈ D.

        ♦ f(x) = f(-x).

    Hàm số y = f(x) có tập xác định là D được gọi là hàm số lẻ nếu:

        ♦ x ∈ D và – x ∈ D.

        ♦ f(x) = - f(-x).

Ví dụ minh họa

Bài 1: Xét tính tuần hoàn và tìm chu kì cơ sở của các hàm số sau:

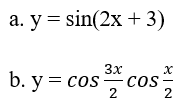
Hướng dẫn giải

a. Hàm số đã cho tuần hoàn với chu kì T = 2π/2 = π.

b.

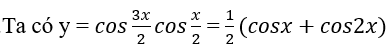
Ta có hàm số y = cosx tuần hoàn với chu kì T = 2 π , hàm số y = cos2x tuần hoàn với chu kì T = π. Vậy hàm số đã cho tuần hoàn với chu kì T = 2 π .

Bài 2: Xét tính tuần hoàn và tìm chu kì cơ sở của các hàm số sau: y = cosx + cos√3x.

Hướng dẫn giải

Giả sử hàm số đã cho tuần hoàn với chu kì T ≠ 0. Khi đó ta có:

cos(x + T) + cos[√3(x +T)] = cosx + cos√3x.

Cho x = 0. Ta có: cosT + cos√3T = 2. Vì cosx ≤ 1 với mọi x nên ta có:

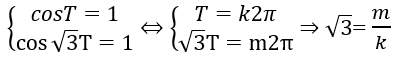
mà m, k ∈ Z (vô lý). Vậy hàm số đã cho không tuần hoàn.

Cách xét Tính đơn điệu của hàm số lượng giác

A. Phương pháp giải

+ Hàm số y= sinx đồng biến trên mỗi khoảng ((- π)/2+k2π; π/2+k2π) và nghịch biến trên mỗi khoảng (( π)/2+k2π; 3π/2+k2π)với k ∈ Z.

+ Hàm số y= cosx đồng biến trên mỗi khoảng (-π+k2π;k2π) và nghịch biến trên mỗi khoảng (k2π; π+k2π ) với k ∈ Z.

+ Hàm số y= tanx đồng biến trên mỗi khoảng ((-π)/2+kπ; π/2+kπ) với k ∈ Z.

+ Hàm số y= cotx nghịch biến trên mỗi khoảng (kπ; π+ kπ)với k ∈ Z.

B. Ví dụ minh họa

Ví dụ 1: Cho hàm số y = sinx. Mệnh đề nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng(π/2;π) , nghịch biến trên khoảng(π;3π/2) .

B. Hàm số đồng biến trên khoảng(-3π/2;-π/2) , nghịch biến trên khoảng(-π/2;π/2) .

C. Hàm số đồng biến trên khoảng(0;π/2) , nghịch biến trên khoảng(-π/2;0) .

D. Hàm số đồng biến trên khoảng(-π/2;π/2) , nghịch biến trên khoảng(π/2;3π/2) .

Lời giải:

Chọn D

Hàm số y= sinx đồng biến khi x thuộc góc phần tư thứ I và thứ IV;

nghịch biến khi x thuộc góc phần tư thứ II và thứ III.

Ví dụ 2: Bảng biến thiên của hàm số y=f(x)=cos2x trên đoạn [-π/2;3π/2] là:

A.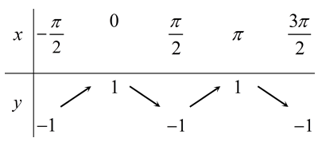

B.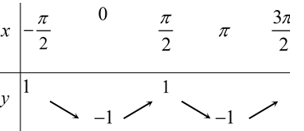

C.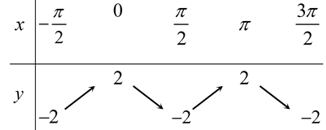

D.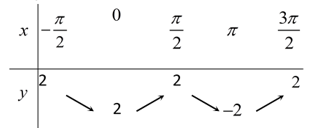

Lời giải:

Chọn A

Ta có thể loại phương án B, C ; D luôn do tại f(0)=cos0=1 và y=f(π)=cos2π=1 .

Các bảng biến thiên B ; C ; D đều không thỏa mãn.