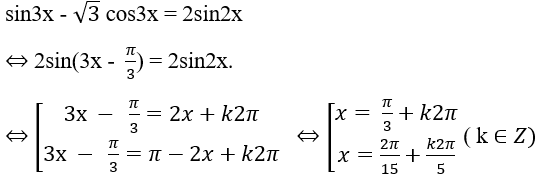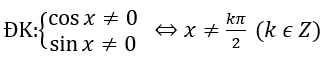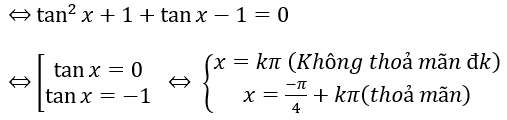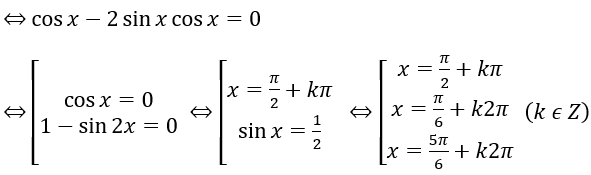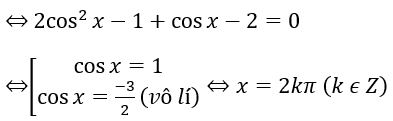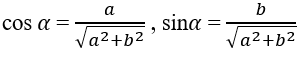Các dạng bài tập Phương trình lượng giác chọn lọc, có lời giải - Toán lớp 11

---

Các dạng bài tập Phương trình lượng giác chọn lọc, có lời giải

Với Các dạng bài tập Phương trình lượng giác chọn lọc, có lời giải Toán lớp 11 tổng hợp các dạng bài tập, 100 bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Phương trình lượng giác từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

• Dạng 1: Cách giải phương trình lượng giác cơ bản Xem chi tiết
• Trắc nghiệm giải phương trình lượng giác cơ bản Xem chi tiết
• Dạng 2: Phương trình bậc hai với một hàm số lượng giác Xem chi tiết
• Trắc nghiệm phương trình bậc hai với một hàm số lượng giác Xem chi tiết
• Dạng 3: Phương trình bậc nhất theo sinx và cosx Xem chi tiết
• Trắc nghiệm phương trình bậc nhất theo sinx và cosx Xem chi tiết
• Dạng 4: Phương trình đẳng cấp bậc 2, bậc 3 lượng giác Xem chi tiết
• Trắc nghiệm phương trình đẳng cấp bậc 2, bậc 3 lượng giác Xem chi tiết
• Dạng 5: Phương trình lượng giác đối xứng, phản đối xứng Xem chi tiết
• Trắc nghiệm phương trình lượng giác đối xứng, phản đối xứng Xem chi tiết
• Dạng 6: Cách giải các phương trình lượng giác đặc biệt Xem chi tiết
• Trắc nghiệm giải các phương trình lượng giác đặc biệt Xem chi tiết
• Dạng 7: Tìm nghiệm của phương trình lượng giác thỏa mãn điều kiện Xem chi tiết
• Trắc nghiệm tìm nghiệm của phương trình lượng giác thỏa mãn điều kiện Xem chi tiết
• Dạng 8: Phương pháp loại nghiệm, hợp nghiệm trong phương trình lượng giác Xem chi tiết
• Trắc nghiệm phương pháp loại nghiệm, hợp nghiệm trong phương trình lượng giác Xem chi tiết
• Giải phương trình lượng giác cơ bản Xem chi tiết
• Tìm nghiệm của phương trình lượng giác cơ bản trên khoảng (đoạn) Xem chi tiết
• Phương trình quy về phương trình lượng giác cơ bản Xem chi tiết
• Phương trình bậc nhất đối với hàm số lượng giác Xem chi tiết
• Phương trình quy về phương trình bậc nhất đối với hàm số lượng giác Xem chi tiết
• Phương trình bậc hai đối với hàm số lượng giác Xem chi tiết
• Phương trình quy về phương trình bậc hai đối với hàm số lượng giác Xem chi tiết
• Tìm nghiệm của phương trình lượng giác trong khoảng, đoạn Xem chi tiết
• Tìm điều kiện của tham số m để phương trình lượng giác có nghiệm Xem chi tiết
• Điều kiện để phương trình bậc nhất đối với sinx và cosx có nghiệm Xem chi tiết
• Giải phương trình bậc nhất đối với sinx và cosx Xem chi tiết
• Phương trình quy về phương trình bậc nhất đối với sinx và cosx Xem chi tiết
• Phương trình thuần nhất bậc 2 đối với sinx và cosx Xem chi tiết
• Phương trình đối xứng, phản đối xứng đối với sinx và cosx Xem chi tiết
• Phương trình lượng giác đưa về dạng tích Xem chi tiết
• Phương trình lượng giác không mẫu mực Xem chi tiết
• Tìm số nghiệm của phương trình lượng giác trong khoảng, đoạn Xem chi tiết

Cách giải phương trình lượng giác cơ bản

A. Phương pháp giải & Ví dụ

- Phương trình sinx = a        (1)

    ♦ |a| > 1: phương trình (1) vô nghiệm.

    ♦ |a| ≤ 1: gọi α là một cung thỏa mãn sinα = a.

Khi đó phương trình (1) có các nghiệm là

                x = α + k2π, k ∈ Z

                và x = π-α + k2π, k ∈ Z.

Nếu α thỏa mãn điều kiện 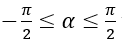và sinα = a thì ta viết α = arcsin a.

Khi đó các nghiệm của phương trình (1) là

                x = arcsina + k2π, k ∈ Z

                và x = π - arcsina + k2π, k ∈ Z.

Các trường hợp đặc biệt:

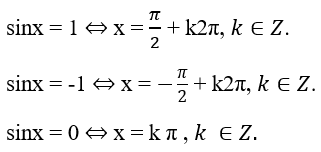
- Phương trình cosx = a        (2)

    ♦ |a| > 1: phương trình (2) vô nghiệm.

    ♦ |a| ≤ 1: gọi α là một cung thỏa mãn cosα = a.

Khi đó phương trình (2) có các nghiệm là

                x = α + k2π, k ∈ Z

                và x = -α + k2π, k ∈ Z.

Nếu α thỏa mãn điều kiện 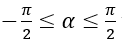và cosα = a thì ta viết α = arccos a.

Khi đó các nghiệm của phương trình (2) là

                x = arccosa + k2π, k ∈ Z

                và x = -arccosa + k2π, k ∈ Z.

Các trường hợp đặc biệt:

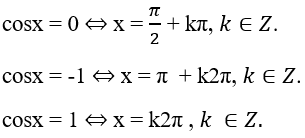
- Phương trình tanx = a        (3)

Điều kiện: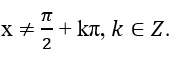

Nếu α thỏa mãn điều kiện 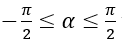và tanα = a thì ta viết α = arctan a.

Khi đó các nghiệm của phương trình (3) là

                x = arctana + kπ,k ∈ Z

- Phương trình cotx = a        (4)

Điều kiện: x ≠ kπ, k ∈ Z.

Nếu α thỏa mãn điều kiện 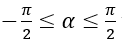và cotα = a thì ta viết α = arccot a.

Khi đó các nghiệm của phương trình (4) là

                x = arccota + kπ, k ∈ Z

Ví dụ minh họa

Bài 1: Giải các phương trình lượng giác sau:

a) sinx = sin(π/6)        c) tanx – 1 = 0

b) 2cosx = 1.        d) cotx = tan2x.

Hướng dẫn:

a) sin⁡x = sin⁡π/6

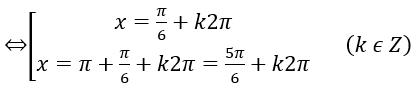
b)

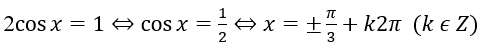
c) tan⁡x=1⇔cos⁡x= π/4+kπ (k ∈ Z)

d) cot⁡x=tan⁡2x

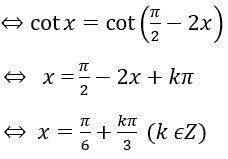
Bài 2: Giải các phương trình lượng giác sau:

a) cos² x - sin2x =0.

b) 2sin(2x – 40º) = √3

Hướng dẫn:

a) cos²x-sin²x=0 ⇔cos²x-2 sin⁡x cos⁡x=0

        ⇔ cos⁡x (cos⁡x - 2 sin⁡x )=0

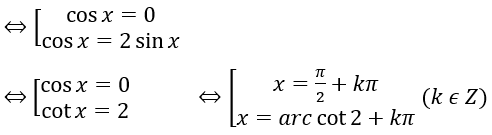
b) 2 sin⁡(2x-40º )=√3

⇔ sin⁡(2x-40º )=√3/2

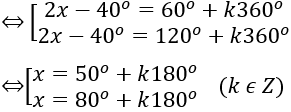
Bài 3: Giải các phương trình lượng giác sau:

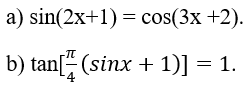
Hướng dẫn:

a) sin⁡(2x+1)=cos⁡(3x+2)

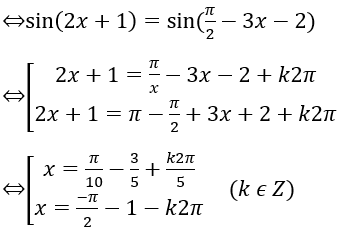
b)

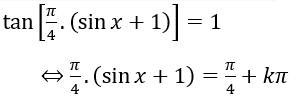
⇔ sin⁡x+1=1+4k

⇔ sin⁡x=4k (k ∈ Z)

Nếu |4k| > 1⇔|k| > 1/4; phương trình vô nghiệm

Nếu |4k| ≤ 1 mà k nguyên ⇒ k = 0 .Khi đó:

        ⇔sin⁡x = 0 ⇔ x = mπ (m ∈ Z)

Cách giải Phương trình bậc hai với một hàm số lượng giác

A. Phương pháp giải & Ví dụ

Định nghĩa:

Phương trình bậc hai đối với một hàm số lượng giác Là phương trình có dạng :

        a.f²(x) + b.f(x) + c = 0

với f(x) = sinu(x) hoặc f(x) = cosu(x), tanu(x), cotu(x).

Cách giải:

Đặt t = f(x) ta có phương trình : at² + bt +c = 0

Giải phương trình này ta tìm được t, từ đó tìm được x

Khi đặt t = sinu(x) hoặc t = cosu(x), ta có điều kiện: -1 ≤ t ≤ 1

Ví dụ minh họa

Bài 1: sin²x +2sinx - 3 = 0

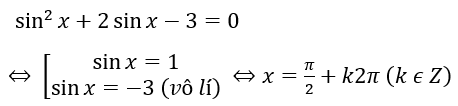
Bài 2: cos2x – sinx + 2 = 0

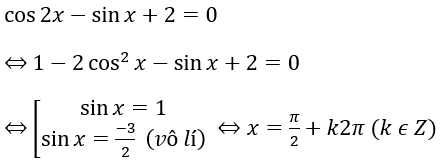
B. Bài tập vận dụng

Bài 1: 1/(sin² x)+tanx-1=0

Lời giải:

Bài 2: cosx – sin2x = 0

Lời giải:

Bài 3: cos2x + cosx – 2 = 0

Lời giải:

Cách giải Phương trình bậc nhất theo sinx và cosx

A. Phương pháp giải & Ví dụ

Xét phương trình asinx + bcosx = c (1) với a, b là các số thực khác 0.

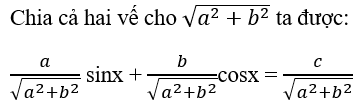
Khi đó phương trình (1) được đưa về dạng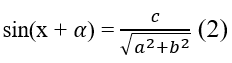

Ở đó α là cung thỏa mãn

Chú ý:

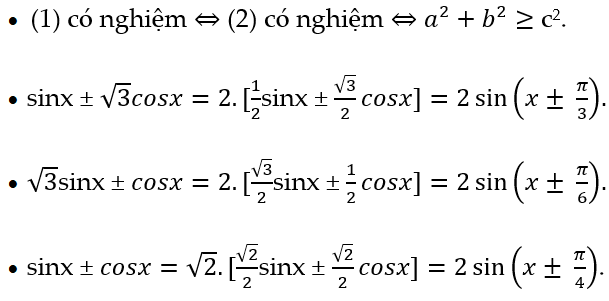
Ví dụ minh họa

Bài 1: Giải phương trình sau: cos²x – sin2x = 0.

Bài 2: Giải phương trình sau: sin3x - √3 cos3x = 2sin2x.