Cho hàm số y = −x^3 + 3x^2 − 4. Mệnh đề nào dưới đây là đúng?

❮ Bài trước Bài sau ❯

Cho hàm số y = −x+ 3x − 4. Mệnh đề nào dưới đây là đúng?

Giải SBT Toán 12 Cánh diều Bài 1: Tính đơn điệu của hàm số

Bài 4 trang 11 SBT Toán 12 Tập 1: Cho hàm số y = −x3 + 3x2 − 4. Mệnh đề nào dưới đây là đúng?

A. Hàm số đồng biến trên khoảng (0; 2).

B. Hàm số nghịch biến trên khoảng (−∞; 2).

C. Hàm số đồng biến trên khoảng (0; +∞).

D. Hàm số nghịch biến trên khoảng (0; 2).

Lời giải:

Đáp án đúng là: A

Ta có: y = −x3 + 3x2 − 4 ⇒y' = −3x2 + 6x.

y' = 0 ⇔ −3x2 + 6x = 0 ⇔ x = 0 hoặc x = 2.

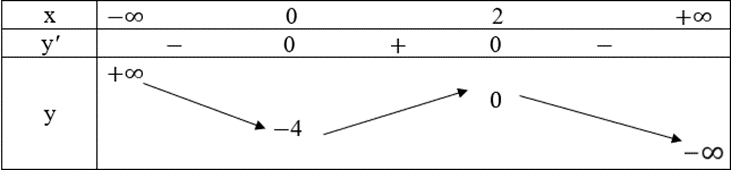
Bảng biến thiên của hàm số:

Cho hàm số y = −x^3 + 3x^2 − 4. Mệnh đề nào dưới đây là đúng?

Căn cứ vào bảng biến thiên, ta có:

Hàm số đồng biến trên khoảng (0; 2);

Hàm số nghịch biến trên các khoảng (−∞; 0) và (2; +∞).

Lời giải SBT Toán 12 Bài 1: Tính đơn điệu của hàm số hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯
2018 © All Rights Reserved.