Bài 2 trang 101 Toán 10 Tập 1 Chân trời sáng tạo

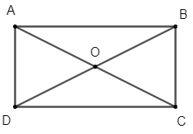
Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính:

Giải Toán lớp 10 Bài 4: Tích vô hướng của hai vectơ

Bài 2 trang 101 Toán lớp 10 Tập 1: Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính:

a) $\vec{A B} . \vec{A O}$ ;

b) $\vec{A B} . \vec{A D}$ .

Lời giải:

Bài 2 trang 101 Toán 10 Tập 1 Chân trời sáng tạo | Giải Toán lớp 10

Vì ABCD là hình chữ nhật nên BC = AD = a, CD = AB = 2a, hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm O của mỗi đường.

Áp dụng định lí Pythagore cho tam giác vuông ABC ta có:

AC² = AB² + BC² = (2a)² + a² = 5a² $\Rightarrow A C = a \sqrt{5}$ .

Do đó: $B D = A C = a \sqrt{5}$ .

Suy ra: $A O = \frac{1}{2} A C = \frac{1}{2} . a \sqrt{5} = \frac{a \sqrt{5}}{2}$ .

Ta có: $co s \hat{B A O} = co s \hat{B A C} = \frac{A B}{A C} = \frac{2 a}{a \sqrt{5}} = \frac{2}{\sqrt{5}}$

a) $\vec{A B} . \vec{A O} = |\vec{A B}| . |\vec{A O}| . c o s (\vec{A B}, \vec{A O}) = A B . A O . \cos \hat{B A O} = 2 a . \frac{a \sqrt{5}}{2} . \frac{2}{\sqrt{5}} = 2 a^{2}$

b) $\vec{A B} . \vec{A D} = |\vec{A B}| . |\vec{A D}| . c o s (\vec{A B}, \vec{A D}) = A B . A D . c o s \hat{B A D}$ = 2a . a . cos90° = 0.

Lời giải bài tập Toán 10 Bài 4: Tích vô hướng của hai vectơ hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯