Hoạt động khám phá 3 trang 65 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán 10
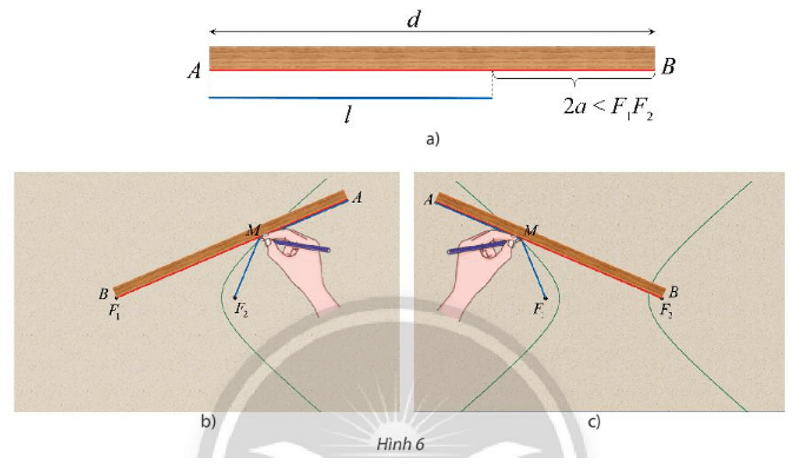
Lấy một tấm bìa, trên đó đánh dấu hai điểm F và F. Lấy một cây thước thẳng với mép thước AB có chiều dài d và một đoạn dây không đàn hồi có chiều dài l sao cho d – l = 2a nhỏ hơn khoảng cách FF (Hình 6a).
Giải Toán lớp 10 Bài 4: Ba đường conic trong mặt phẳng toạ độ
Hoạt động khám phá 3 trang 65 Toán lớp 10 Tập 2: Lấy một tấm bìa, trên đó đánh dấu hai điểm F1 và F2. Lấy một cây thước thẳng với mép thước AB có chiều dài d và một đoạn dây không đàn hồi có chiều dài l sao cho d – l = 2a nhỏ hơn khoảng cách F1F2 (Hình 6a).
Đính một đầu dây vào đầu A của thước, dùng đinh ghim đầu dây còn lại vào điểm F2. Đặt thước sao cho đầu B của thước trùng với điểm F1 và đoạn thẳng BA có thể quay quanh F1. Tựa đầu bút chì M vào đoạn dây, di chuyển điểm M trên tấm bìa và giữ sao cho dây luôn căng, đoạn AM ép sát vào thước, khi đó M sẽ vạch ra trên tấm bìa một đường (H) (xem Hình 6b).
a) Chứng tỏ rằng khi M di động, ta luôn có MF1 – MF2 = 2a.
b) Vẫn đính một đầu dây vào đầu A của thước nhưng đổi chỗ cố định đầu dây còn lại vào F1, đầu B của thước trùng với F2 sao cho đoạn thẳng BA có thể quay quanh F2 và làm tương tự như lần đầu để đầu bút chì M vẽ được một nhánh khác của đường H (Hình 6c). Tính MF2 – MF1.
Lời giải:
a) Ta có:
MF1 + MA = AB = d (1)
MF2 + MA = l (2)
Lấy vế với vế của (1) trừ cho (2) ta được: (MF1 + MA) – (MF2 + MA) = d – l
⇔ MF1 + MA – MF2 – MA = d – l
⇔ MF1 – MF2 = d – l
Mà d – l = 2a.
⇒ MF1 – MF2 = 2a.
Vậy MF1 – MF2 = 2a.
b) Ta có:
MF2 + MA = AB = d (3)
MF1 + MA = l (4)
Lấy vế với vế của (3) trừ cho (4) ta được: (MF2 + MA) – (MF1 + MA) = d – l
⇔ MF2 + MA – MF1 – MA = d – l
⇔ MF2 – MF1 = d – l
Mà d – l = 2a.
⇒ MF2 – MF1 = 2a.
Vậy MF2 – MF1 = 2a.
Lời giải bài tập Toán 10 Bài 4: Ba đường conic trong mặt phẳng toạ độ hay, chi tiết khác:

