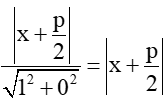Hoạt động khám phá 6 trang 68 Toán lớp 10 Tập 2 Chân trời sáng tạo | Giải Toán 10
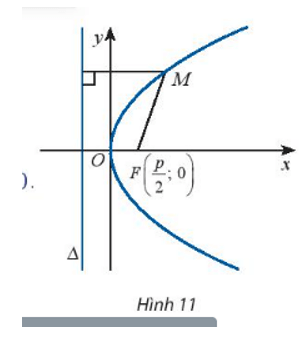
Cho parabol (P) có tiêu điểm F và đường chuẩn ∆. Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên p > 0.
Giải Toán lớp 10 Bài 4: Ba đường conic trong mặt phẳng toạ độ
Hoạt động khám phá 6 trang 68 Toán lớp 10 Tập 2: Cho parabol (P) có tiêu điểm F và đường chuẩn ∆. Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên p > 0.
Chọn hệ trục tọa độ Oxy sao cho và ∆: x + = 0. Xét điểm M(x; y).
a) Tính MF và d(M. ∆).
b) Giải thích phát biểu sau:
M(x; y) ∈ (P) ⇔ 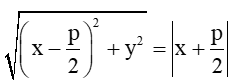
Lời giải:
a) Ta có: ⇒ MF =
Khoảng cách từ điểm M đến đường thẳng ∆ là:
d(M, ∆) =
b) +) Ta có M(x; y) ∈ (P) cần chứng minh 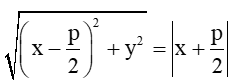
Vì M(x; y) ∈ (P) nên M cách đều F và ∆
⇒ MF = d(M, ∆) hay 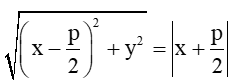
+) Ta có điểm M(x; y) thỏa mãn 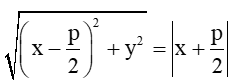
Ta có
⇒ MF = d(M, ∆)
Nghĩa là điểm M thỏa mãn cách đều tiêu điểm F và đường chuẩn ∆. Do đó điểm M thuộc parabol (P) (2)
Từ (1) và (2) suy ra điều phải chứng minh.
Lời giải bài tập Toán 10 Bài 4: Ba đường conic trong mặt phẳng toạ độ hay, chi tiết khác: