Bài 7.17 trang 53 Toán 11 Tập 2 - Kết nối tri thức

---

Giải Toán 11 Bài 25: Hai mặt phẳng vuông góc - Kết nối tri thức

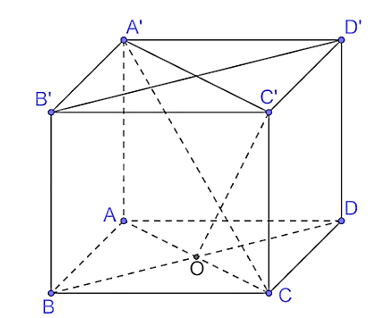
Bài 7.17 trang 53 Toán 11 Tập 2: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a.

a) Tính độ dài đường chéo của hình lập phương.

b) Chứng minh rằng (ACC'A') ⊥ (BDD'B').

c) Gọi O là tâm của hình vuông ABCD. Chứng minh rằng $\widehat{CO{C}^{\text{'}}}$ là một góc phẳng của góc nhị diện [C, BD, C']. Tính (gần đúng) số đo của các góc nhị diện [C, BD, C'], [A, BD,C'].

Lời giải:

a) Vì ABCD.A'B'C'D' là hình lập phương nên có các mặt là hình vuông.

Xét tam giác ABC vuông tại B, có $AC=\sqrt{A{B}^2+B{C}^2}=\sqrt{a^2+a^2}=a\sqrt{2}$.

Vì AA' ⊥ (ABCD) nên AA' ⊥ AC.

Xét tam giác A'AC vuông tại A, có $A^{\text{'}}C=\sqrt{A{A^{\text{'}}}^2+A{C}^2}=\sqrt{a^2+2a^2}=a\sqrt{3}$.

Vậy đường chéo của hình lập phương có độ dài là $a\sqrt{3}$.

b) Vì AA' ⊥ (ABCD) nên AA' ⊥ BD.

Vì ABCD là hình vuông nên AC ⊥ BD mà AA' ⊥ BD, suy ra BD ⊥ (ACC'A').

Vì BD ⊥ (ACC'A') nên (ACC'A') ⊥ (BDD'B').

c) Vì BD ⊥ (ACC'A') nên BD ⊥ C'O mà CO ⊥ BD (do AC ⊥ BD) nên $\widehat{CO{C}^{\text{'}}}$là góc phẳng nhị diện của góc nhị diện [C, BD, C'].

Do ABCD là hình vuông nên O là trung điểm của AC, suy ra $AO=OC=\frac{AC}{2}=\frac{a\sqrt{2}}{2}$.

Xét tam giác C'CO vuông tại C, có $\tan \widehat{C^{\text{'}}OC}=\frac{C{C}^{\text{'}}}{CO}=\frac{a}{\frac{a\sqrt{2}}{2}}=\sqrt{2}$ $\Rightarrow \widehat{C^{\text{'}}OC}\approx 55°$.

Vậy số đo của các góc nhị diện [C, BD, C'] khoảng 55°.

Vì AO ⊥ BD (do AC ⊥ BD), BD ⊥ C'O nên $\widehat{AO{C}^{\text{'}}}$ là góc phẳng nhị diện của góc nhị diện [A, BD,C'].

Vì $\widehat{AO{C}^{\text{'}}}+\widehat{C^{\text{'}}OC}=180°$nên $\widehat{AO{C}^{\text{'}}}=180°-\widehat{C^{\text{'}}OC}\approx 180°-55°=125°$.

Vậy số đo góc nhị diện [A, BD,C'] khoảng 125°.

Lời giải bài tập Toán 11 Bài 25: Hai mặt phẳng vuông góc hay, chi tiết khác:

• HĐ1 trang 44 Toán 11 Tập 2: Cho hai mặt phẳng (P) và (Q). Lấy hai đường thẳng a, a' cùng vuông góc ....

• Câu hỏi trang 44 Toán 11 Tập 2: Góc giữa hai mặt phẳng bằng 0° khi nào, khác 0° khi nào? ....

• Luyện tập 1 trang 45 Toán 11 Tập 2: : Cho hình chóp S.ABCD, đáy ABCD là một hình chữ nhật có tâm O, SO ⊥ (ABCD) ....

• HĐ2 trang 45 Toán 11 Tập 2: Cho mặt phẳng (P) chứa đường thẳng b vuông góc với mặt phẳng (Q) ....

• Luyện tập 2 trang 46 Toán 11 Tập 2: Trong HĐ1 của Bài 23, ta đã nhận ra rằng đường thẳng nối các bản lề của cửa phòng vuông góc ....

• HĐ3 trang 46 Toán 11 Tập 2: Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Kẻ đường thẳng a thuộc (P) ....

• HĐ4 trang 46 Toán 11 Tập 2: Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến a và cùng vuông góc ....

• Luyện tập 3 trang 47 Toán 11 Tập 2: Với giả thiết như ở Ví dụ 3, Cho hình chóp S.ABCD có đáy là hình chữ nhật ....

• HĐ5 trang 47 Toán 11 Tập 2: Một tài liệu hướng dẫn rằng đối với ghế bàn ăn, nên thiết kế lưng ghế tạo ....

• Luyện tập 4 trang 48 Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC), AB = AC = a ....

• Vận dụng 1 trang 48 Toán 11 Tập 2: Trong cửa sổ ở Hình 7.56, cánh và khung cửa là các nửa hình tròn có đường kính 80 ....

• HĐ6 trang 49 Toán 11 Tập 2: Các mặt bên của lăng trụ đứng là các hình gì và các mặt bên đó có vuông góc ....

• HĐ7 trang 49 Toán 11 Tập 2: Các mặt bên của hình lăng trụ đều có phải là các hình chữ nhật có cùng kích thước ....

• HĐ8 trang 49 Toán 11 Tập 2: Trong 6 mặt của hình hộp đứng, có ít nhất bao nhiêu mặt là hình chữ nhật? Vì sao? ....

• HĐ9 trang 50 Toán 11 Tập 2: a) Hình hộp chữ nhật có bao nhiêu mặt là hình chữ nhật? Vì sao? ....

• HĐ10 trang 50 Toán 11 Tập 2: Các mặt của một hình lập phương là các hình gì? Vì sao? ....

• Vận dụng 2 trang 50 Toán 11 Tập 2: Từ một tấm tôn hình chữ nhật, tại 4 góc bác Hùng cắt bỏ đi 4 hình vuông ....

• HĐ11 trang 51 Toán 11 Tập 2: Tháp lớn tại Bảo tàng Louvre ở Paris (H.7.66) (với kết cấu kính và kim loại) ....

• HĐ12 trang 51 Toán 11 Tập 2: Cho hình chóp $S.A_1{A}_2\dots A_n$ . Gọi O là hình chiếu của S trên mặt phẳng ....

• Luyện tập 5 trang 51 Toán 11 Tập 2: Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng ....

• HĐ13 trang 52 Toán 11 Tập 2: : Cho hình chóp đều $S.A_1{A}_2\dots A_n$ . Một mặt phẳng không đi qua S và song song ....

• Câu hỏi trang 52 Toán 11 Tập 2: Hình chóp cụt đều có các cạnh bên bằng nhau hay không? ....

• Bài 7.16 trang 53 Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H là hình chiếu của A trên BC. ....

• Bài 7.18 trang 53 Toán 11 Tập 2: Cho hình hộp chữ nhật ABCD.A'B'C'D' ....

• Bài 7.19 trang 53 Toán 11 Tập 2: Cho hình chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b ....

• Bài 7.20 trang 53 Toán 11 Tập 2: Hai mái nhà trong Hình 7.72 là hai hình chữ nhật. Giả sử AB = 4,8 m ....

• Bài 7.21 trang 53 Toán 11 Tập 2: Độ dốc của mái nhà, mặt sân, con đường thẳng là tang của góc tạo bởi mái nhà ....