HĐ4 trang 84 Toán 11 Tập 2 - Kết nối tri thức

Nhận biết tiếp tuyến của đồ thị hàm số

Giải Toán 11 Bài 31: Định nghĩa và ý nghĩa của đạo hàm - Kết nối tri thức

HĐ4 trang 84 Toán 11 Tập 2: Nhận biết tiếp tuyến của đồ thị hàm số

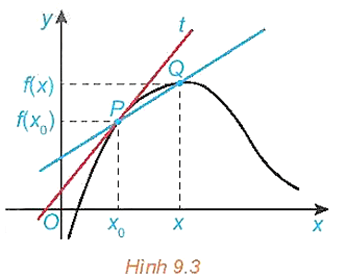
Cho hàm số y = f(x) có đồ thị (C) và P(x₀; f(x₀)) ∈ (C). Xét điểm Q(x; f(x)) thay đổi trên (C) với x ≠ x₀.

a) Đường thẳng đi qua hai điểm P, Q được gọi là một cát tuyến của đồ thị (C) (H.9.3). Tìm hệ số góc k_PQ của cát tuyến PQ.

b) Khi x → x₀ thì vị trí của điểm Q(x; f(x)) trên đồ thị (C) thay đổi như thế nào ?

c) Nếu điểm Q di chuyển trên (C) tới điểm P mà k_PQcó giới hạn hữu hạn k thì có nhận xét gì về vị trí giới hạn của cát tuyến QP?

Lời giải:

a) Ta có: $\overrightarrow{PQ}=\left(x-x_0;f\left(x\right)-f\left(x_0\right)\right)$ . Suy ra ${\overrightarrow{n}}_{PQ}=\left(f\left(x\right)-f\left(x_0\right);x_0-x\right)$ .

Phương trình đường thẳng PQ là

[f(x) – f(x₀)](x – x₀) + (x_0­ – x)[y – f(x₀)] = 0

Hay [f(x) – f(x₀)]x – (x – x₀)y – f(x)x₀ + xf(x₀) = 0

Tức là y = $\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}x+\frac{xf\left(x_0\right)-x_{0}f\left(x\right)}{x-x_0}$ .

Do đó, hệ số góc của cát tuyến PQ là $k_{PQ}=\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$ .

b)

Khi x$\to$x_o thì vị trí của điểm Q(x; f(x)) trên đồ thị (C) sẽ tiến gần đến điểm P(x₀; f(x₀)) và khi x = x₀ hai điểm này sẽ trùng nhau.

c)

Nếu điểm Q di chuyển trên (C) tới điểm P mà k_PQ có giới hạn hữu hạn k thì cát tuyến PQ cũng sẽ tiến gần đến gần vị trí tiếp tuyến của đồ thị (C) tại điểm P. Vì vậy giới hạn của cát tuyến QP sẽ là đường thẳng tiếp tuyến tại điểm P.

Lời giải bài tập Toán 11 Bài 31: Định nghĩa và ý nghĩa của đạo hàm hay, chi tiết khác:

• Mở đầu trang 81 Toán 11 Tập 2: Nếu một quả bóng được thả rơi tự do từ đài quan sát trên sân thượng ....

• HĐ1 trang 81 Toán 11 Tập 2: Một vật di chuyển trên một đường thẳng (H.9.2) ....

• HĐ2 trang 82 Toán 11 Tập 2: Điện lượng Q truyền trong dây dẫn là một hàm số của thời gian t ....

• Luyện tập 1 trang 83 Toán 11 Tập 2: Tính đạo hàm của hàm số y = –x² + 2x + 1 tại điểm x₀ = –1 ....

• HĐ3 trang 83 Toán 11 Tập 2: Tính đạo hàm f'(x0) tại điểm x0 bất kì trong các trường hợp sau ....

• Luyện tập 2 trang 84 Toán 11 Tập 2: a) y = x² + 1 ....

• Luyện tập 3 trang 85 Toán 11 Tập 2: Tìm hệ số góc của tiếp tuyến của parabol y = x² tại điểm ....

• HĐ5 trang 85 Toán 11 Tập 2: Cho hàm số y = x² có đồ thị là đường parabol (P) ....

• Luyện tập 4 trang 85 Toán 11 Tập 2: Viết phương trình tiếp tuyến của parabol (P): y = –2x² ....

• Vận dụng trang 85 Toán 11 Tập 2: Người ta xây dựng một cây cầu vượt giao thông hình parabol nối hai điểm ....

• Bài 9.1 trang 86 Toán 11 Tập 2: Tính (bằng định nghĩa) đạo hàm của các hàm số sau ....

• Bài 9.2 trang 86 Toán 11 Tập 2: Sử dụng định nghĩa, tính đạo hàm của các hàm số sau ....

• Bài 9.3 trang 86 Toán 11 Tập 2: Viết phương trình tiếp tuyến của parabol ....

• Bài 9.4 trang 86 Toán 11 Tập 2: Một vật được phóng theo phương thẳng đứng lên trên từ mặt đất ....

• Bài 9.5 trang 86 Toán 11 Tập 2: Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó ....