Lý thuyết Toán 8 Chân trời sáng tạo Bài 1: Định lí Pythagore

---

Haylamdo biên soạn và sưu tầm tóm tắt lý thuyết Toán 8 Bài 1: Định lí Pythagore sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Lý thuyết Toán 8 Chân trời sáng tạo Bài 1: Định lí Pythagore

A. Lý thuyết

1. Định lí Pythagore

Định lí Pythagore:

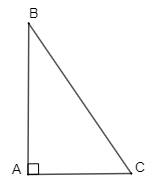
Trong một tam giác vuông, bình phương độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.

GT	∆ABC, $\hat{A}=90°$
KL	BC2 = AB2 + AC2

Ví dụ 1.

a) Cho một hình tam giác vuông có hai cạnh góc vuông là a = 5 cm, b = 6 cm. Tính độ dài cạnh huyền của tam giác vuông đó.

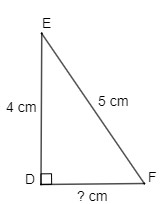
b) Cho tam giác vuông DEF có cạnh huyền EF = 5 cm và cạnh DE = 4 cm. Tính độ dài cạnh DF.

Hướng dẫn giải

a) Gọi c là độ dài cạnh huyền của tam giác vuông đã cho. Áp dụng định lí Pythagore, ta có:

c² = a² + b² = 5² + 6² = 25 + 36 = 61.

Vậy độ dài cạnh huyền của tam giác đó là c = $\sqrt{61}$ cm.

b)

Áp dụng định lí Pythagore vào tam giác vuông DEF có cạnh huyền EF, ta có:

EF² = DE² + DF²

Suy ra DF² = EF² – DE² = 5² – 4² = 25 – 16 = 9 = 3².

Vậy cạnh DF dài 3 cm.

2. Định lí Pythagore đảo

Định lí Pythagore đảo:

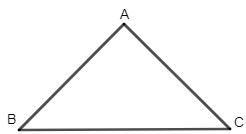
Nếu một tam giác có bình phương độ dài của một cạnh bằng tổng các bình phương độ dài của hai cạnh kia thì tam giác đó là tam giác vuông.

GT	∆ABC, BC2 = AB2 + AC2
KL	$\hat{A}=90°$

Ví dụ 2. Các tam giác sau có phải là tam giác vuông không?

a) Tam giác ABC có AB = 6 m, BC = 8 m, AC = 10 m.

b) Tam giác DEF có DE = 4 dm, DF = 10 dm, EF = 6 dm.

Hướng dẫn giải

a) Ta có: 10² = 6² + 8², suy ra AC² = AB² + BC².

Vậy tam giác ABC vuông tại B.

b) Ta có DF là cạnh dài nhất và 10² ≠ 4² + 6², suy ra DF² ≠ DE² + EF².

Vậy tam giác DEF không phải là tam giác vuông.

3. Vận dụng định lí Pythagore

Ta có thể vận dụng định lí Pythagore để tính nhiều yếu tố khoa học và đời sống như tính độ dài đoạn thẳng, khoảng cách giữa hai điểm, chiều dài, chiều cao của vật, …

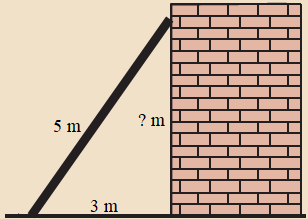
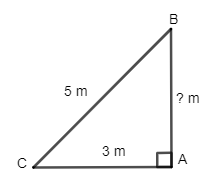
Ví dụ 3. Một cái thang dài 5 m đang dựa vào một bức tường, chân thang cách chân tường 3 m (hình vẽ). Tính chiều cao mà thang có thể vươn tới.

Hướng dẫn giải

Gọi AC là khoảng cách từ chân thang đến chân tường; BC là độ dài của thang và AB là chiều cao thang có thể vươn tới.

Ta được tam giác vuông ABC như hình dưới.

Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:

BC² = AB² + AC²

Suy ra AB² = BC² – AC² = 5² – 3² = 25 – 9 = 16 = 4².

Vậy chiều cao mà thang có thể vươn tới là AB = 4 m.

B. Bài tập tự luyện

Bài 1. Cho tam giác ABC vuông tại A.

a) Tính độ dài cạnh AB nếu biết BC = 20 dm, AC = 12 dm.

b) Tính độ dài cạnh AC nếu biết BC = 8 m, AB = $\sqrt{15}$ m.

c) Tính độ dài cạnh BC nếu biết AB = 12 cm, AC = 9 cm.

Hướng dẫn giải

Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:

BC² = AB² + AC²

a) AB² = BC² – AC² = 20² – 12² = 400 – 144 = 256 = 16².

Vậy cạnh AB dài 16 dm.

b) AC² = BC² – AB² = 8² – ${\left(\sqrt{15}\right)}^2$ = 64 – 15 = 49 = 7².

Vậy cạnh AC dài 7 m.

c) BC² = AB² + AC² = 12² + 9² = 144 + 81 = 225 = 15².

Vậy cạnh BC dài 15 cm.

Bài 2. Chứng minh tam giác ABC vuông trong các trường hợp sau:

a) AB = 10 cm, AC = 8 cm, BC = 6 cm.

b) AB = 8 dm, AC = 15 dm, BC = 17 dm.

Hướng dẫn giải

a) Ta có: 10² = 8² + 6², suy ra AB² = AC² + BC².

Vậy tam giác ABC là tam giác vuông tại C.

b) Ta có: 17² = 8² + 15², suy ra BC² = AB² + AC²

Vậy tam giác ABC là tam giác vuông tại A.

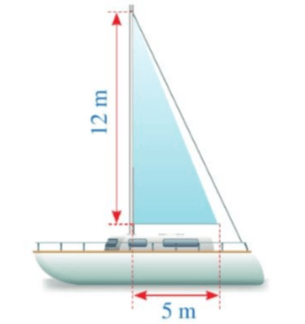
Bài 3. Hình dưới mô tả một cánh buồm có dạng tam giác vuông, được buộc vào cột buồm thẳng đứng, với độ dài hai cạnh góc vuông là 12 m và 5 m (hình vẽ).

a) Tính độ dài cạnh huyền của cánh buồm.

b) Vật liệu dùng để làm cánh buồm là vải. Tính diện tích vải dùng để làm một cánh buồm như vậy.

Hướng dẫn giải

a) Gọi x là độ dài cạnh huyền của cánh buồm.

Áp dụng định lí Pythagore cho tam giác vuông, ta có:

x² = 12² + 5² = 144 + 25 = 169 = 13²

Vậy độ dài cạnh huyền của cánh buồm là 13 m.

b) Diện tích vải dùng để làm cánh buồm đó là: $\frac{5.12}{2}$ = 30 (m²).