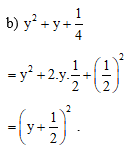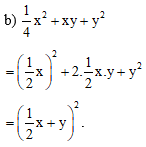Lý thuyết Toán 8 Chân trời sáng tạo Bài 3: Hằng đẳng thức đáng nhớ

---

Haylamdo biên soạn và sưu tầm tóm tắt lý thuyết Toán 8 Bài 3: Hằng đẳng thức đáng nhớ sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Lý thuyết Toán 8 Chân trời sáng tạo Bài 3: Hằng đẳng thức đáng nhớ

A. Lý thuyết

1. Bình phương của một tổng, một hiệu

– Hai biểu thức (đại số) A và B có giá trị bằng nhau với bất kì giá trị nào của các biến thì ta nói hai biểu thức A và B bằng nhau hoặc đồng nhất với nhau.

Ta viết A = B, là một đồng nhất thức hoặc hằng đẳng thức.

– Với hai biểu thức tùy ý A và B, ta có:

Ví dụ 1.Tính:

a) (2x + y)²;

b) (3x² – 2y)².

Hướng dẫn giải.

a) (2x + y)² = (2x)² + 2 . 2x . y + y² = 4x² + 4xy + y²;

b) (3x² – 2y)² = (3x²)² – 2 . 3x² . 2y + (2y)² = 9x⁴ – 12x²y + 4y².

Ví dụ 2. Viết các biểu thức sau thành bình phương của một tổng hoặc một hiệu:

a) x² – 4xy + 4y²;

b) $y^2+y+\frac{1}{4}$

Hướng dẫn giải

a) x² – 4xy + 4y²

= x² – 2 . x . 2y + (2y)²

= (x – 2y)²;

Ví dụ 3. Tính nhanh:

a) 99²;

b) 101².

Hướng dẫn giải

a) 99²

= (100 – 1)²

= 100² – 2 . 100 . 1 + 1²

= 10 000 – 200 + 1

= 9801;

b) 101²

= (100 + 1)²

= 100² + 2 . 100 . 1 + 1²

= 10 000 + 200 + 1

= 10 201.

2. Hiệu của hai bình phương

Với hai biểu thức tùy ý A và B, ta có:

Ví dụ 4.Thực hiện các phép nhân:

a) (x + 3)(x – 3).

b) (2x + y)(2x – y).

c) (x² – 2y)(x² + 2y).

Hướng dẫn giải.

a) (x + 3)(x – 3) = x² – 3² = x² – 9.

b) (2x + y)(2x – y) = (2x)² – y² = 4x² – y².

c) (x² – 2y)(x² + 2y) = (x²)² – (2y)² = x⁴ – 4y².

Ví dụ 5. Tính nhanh:

a) 38 . 42;

b) 80² – 20².

Hướng dẫn giải

a) 38 . 42 = (40 – 2)(40 + 2) = 40² – 2² = 1 600 – 4 = 1 596;

b) 80² – 20² = (80 + 20)(80 – 20) = 100 . 60 = 6 000.

3. Lập phương của một tổng, một hiệu

Với hai biểu thức tùy ý A và B, ta có:

Ví dụ 6.Tính:

b) (x + 3y)³.

a) (x – 5)³.

Hướng dẫn giải.

a) (x – 5)³

= x³ – 3 . x² . 5 + 3 . x . 5² – 5³

= x³ – 15x² + 75x – 125.

b) (x + 3y)³

= x³ + 3 . x² . 3y + 3 . x . (3y)² + (3y)³

= x³ + 9x²y + 27xy² + 27y³.

4. Tổng và hiệu của hai lập phương

Với hai biểu thức tùy ý A và B, ta có:

Ví dụ 7. Viết các đa thức sau dưới dạng tích:

a) x³ + 1;

b) y³ – 216.

Hướng dẫn giải.

a) x³ + 1 = x³ + 1³

= (x + 1)(x² – x . 1 + 1²)

= (x + 1)(x² – x + 1);

b) y³ – 216 = y³ – 6³

= (y – 6)(y² + y . 6 + 6²)

= (y – 6)(y² + 6y + 36).

Ví dụ 8. Tính

a) (2x + 3)(4x² – 6x + 9);

b) (y – 5)(y² + 5y + 25).

Hướng dẫn giải.

a) (2x + 3)(4x² – 6x + 9)

= (2x + 3)[(2x)² – 2x . 3 + 3²]

= (2x)³ + 3³

= 8x³ + 27;

b) (y – 5)(y² + 5y + 25)

= (y – 5)(y² + 5 . y + 5²)

= y³ – 5³

= y³ – 125.

B. Bài tập tự luyện

Bài 1.Viết các biểu thức sau thành đa thức

a) (3x + 7y)²;

b) (x – 5y)²;

c) (x – 3y)(x + 3y);

d) (2a – b)(4a² + 2ab + b²);

e) (a – 2)(a² + 4)(a + 2);

f) (a + 5b)(a² + 5ab + 25b²);

g) (–x + y)³;

h) (–x – xy)³.

Hướng dẫn giải

a) (3x + 7y)²

= (3x)² + 2 . 3x . 7y + (7y)²

= 9x² + 42xy + 49y²;

b) (x – 5y)²

= x² – 2 . x . 5 y + (5y)²

= x² – 10xy + 25y²;

c) (x – 3y)(x + 3y)

= x² – (3y)²

= x² – 9y².

d) (2a – b)(4a² + 2ab + b²)

= (2a – b)[(2a)² + 2a . b + b²]

= (2a – b)³;

e) (a – 2)(a² + 4)(a + 2)

= [(a – 2)(a + 2)](a² + 4)

= (a² – 4)(a² + 4)

= (a²)² – 4²

= a⁴ – 16;

f) (a + 5b)(a² + 5ab + 25b²)

= (a + 5b)[a² + a . 5b + (5b)²]

= (a + 5b)³.

g) (–x + y)³

= (–x)³ + 3.(–x)²y + 3(–x).y² + y³

= –x³ + 3x²y – 3xy² + y³.

h) (–x – xy)³

= (–x)³ – 3.(–x)²xy + 3.(–x).(xy)² – (xy)³

= –x³ – 3x³y – 3x³y² – x³y³.

Bài 2.Viết các biểu thức sau thành bình phương hoặc lập phương của một tổng hay một hiệu:

a) 9x² + 6x + 1;

b) $\frac{1}{4}{x}^2+xy+y^2$

c) x³ – 3x² + 3x – 1;

d) x³ + 9x²y + 27xy² + 27y³.

Hướng dẫn giải

a) 9x² + 6x + 1

= (3x)² + 2 . 3x . 1 + 1²

= (3x + 1)²;

c) x³ – 3x² + 3x – 1

= (x – 1)³;

d) x³ + 9x²y + 27xy² + 27y³

= x³ + 3.x².3y + 3.x.(3y)² + (3y)³

= (x + 3y)³.

Bài 3.Tính nhanh:

a) 98²;

b) 45 . 55;

c) 67² – 33².

Hướng dẫn giải

a) 98²

= (100 – 2)²

= 100² – 2 . 100 . 2 + 2²

= 10 000 – 400 + 4

= 9 604;

b) 45 . 55

= (50 – 5)(50 + 5)

= 50² – 5²

= 2 500 – 25

= 2 475;

c) 67² – 33²

= (67 – 33)(67 + 33)

= 34 . 100

= 3 400.

Bài 4.Cho x + y = 3, xy = 10. Tính:

a) A = x³ + y³;

b) B = (x – y)².

Hướng dẫn giải

a) A = x³ + y³

= (x + y)(x² – xy + y²)

= (x + y)(x² + 2xy + y² – 3xy)

= (x + y)[(x + y)² – 3xy]

Thay x + y = 3, xy = 10 vào biểu thức A ta có

A = 3 . (3² – 3 . 10) = 3 . (9 – 30) = 3 . (–21) = –63.

b) B = (x – y)²

= x² – 2xy + y²

= x² + 2xy + y² – 4xy

= (x + y)² – 4xy

Thay x + y = 3, xy = 10 vào biểu thức B ta có

B = 3² – 4 . 10 = 9 – 40 = –31.

Bài 5.Cho hình lập phương có cạnh bằng 3 cm. Thể tích hình lập phương sẽ tăng bao nhiêu nếu các cạnh đều tăng a cm?

Hướng dẫn giải

Thể tích hình lập phương là

V = 3 . 3 . 3 = 27 (cm³)

Khi các cạnh đều tăng thêm a cm thì độ dài các cạnh của hình lập phương là3 + a (cm)

Thể tích hình lập phương mới là

V = (3 + a)(3 + a)(3 + a)

= (3 + a)³

= 3³ + 3 . 3² . a + 3 . 3 . a² + a³

= a³ + 9a² + 27a + 27 (cm³)

Thể tích hình lập phương sẽ tăng thêm là

a³ + 9a² + 27a + 27 – 27 = a³ + 9a² + 27a (cm³)

Vậy thể tích hình lập phương sẽ tăng thêm a³ + 9a² + 27a cm³.