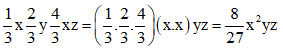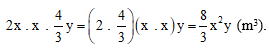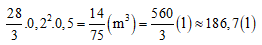Lý thuyết Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến

---

Haylamdo biên soạn và sưu tầm tóm tắt lý thuyết Toán 8 Bài 1: Đơn thức và đa thức nhiều biến sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Lý thuyết Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến

A. Lý thuyết

1. Đơn thức và đa thức

– Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.

– Đa thức là một tổng của những đơn thức. Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.

Chú ý:

• Mỗi đơn thức cũng được coi là một đa thức (chỉ chứa một hạng tử).

• Số 0 được gọi đơn thức không, cũng gọi là đa thức không.

Ví dụ 1.Cho các biểu thức sau:

$\frac{2\text{x}}{y};12y;\sqrt{10};x^2+2\text{x}+y;\frac{2}{3}xy+y^2;5{\text{x}}^{2}yz$.

Trong số các biểu thức trên, hãy chỉ ra:

a) Các đơn thức;

b) Các đa thức và số hạng tử của chúng.

Hướng dẫn giải

a) Các đơn thức là: $12y;\sqrt{10};5{\text{x}}^{2}yz.$

b) Các đa thức gồm:

+ Các đơn thức $12y;\sqrt{10};5{\text{x}}^{2}yz.$đều có một hạng tử.

+ Đa thức x² + 2x + y có ba hạng tử và $\frac{2}{3}xy+y^2$có hai hạng tử.

Ví dụ 2.Tính giá trị của các đơn thức, đa thức sau tại x = 1, y = –2.

a) 5xy.

b) $\frac{1}{2}{x}^{2}y+y^2+x$.

Hướng dẫn giải

a) Thay x = 1, y = –2 vào đơn thức 5xy ta được 5 . 1 . (–2) = –10.

b) Thay x = 1, y = –2 vào đa thức $\frac{1}{2}{x}^{2}y+y^2+x$ta được

$\frac{1}{2}{.1}^2.\left(-2\right)+{\left(-2\right)}^2+1=-1+4+1=4.$

2. Đơn thức thu gọn

Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến chỉ xuất hiện một lần dưới dạng nâng lên lũy thừa với số mũ nguyên dương.

Thừa số là một số nói trên được gọi là hệ số, tích của các thừa số còn lại phần biến của đơn thức thu gọn.

Chú ý:

• Tổng số mũ của tất cả các biến có trong đơn thức (có hệ số khác 0) gọi là bậc của đơn thức đó.

• Ta coi một số khác 0 là đơn thức thu gọn, có hệ số bằng chính số đó và có bậc bằng 0.

• Đơn thức không (số 0) không có bậc.

• Khi viết đơn thức thu gọn ta thường viết hệ số trước, phần biến sau và các biến được viết theo thứ tự bảng chữ cái.

Ví dụ 3.Đơn thức nào sau đây là đơn thức thu gọn? Chỉ ra hệ số và bậc của mỗi đơn thức đó? Hãy thu gọn các đơn thức còn lại.

$-2\text{x}yz;\sqrt{10}{x}^{2}y{z}^3;3{\text{x}}^{2}yz.7yz;\frac{3}{4}$

Hướng dẫn giải

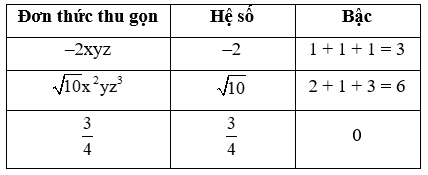
Các đơn thức thu gọn là

–2xyz, có hệ số là – 2, bậc bằng 1 + 1 + 1 = 3;

$\sqrt{10}{x}^{2}y{z}^3$, có hệ số là $\sqrt{10}$, bậc bằng 2 + 1 + 3 = 6;

$\frac{3}{4}$, có hệ số là $\frac{3}{4}$, bậc bằng 0

3x²yz . 7yz không phải là đơn thức thu gọn vì trong tích 3x²yz . 7yz có hai số là 3 và 7, các biến y, z xuất hiện hai lần

Thu gọn đơn thức:

3x²yz . 7yz = (3 . 7)x² (y . y)(z . z) = 21x²y²z².

Các đơn thức thu gọn là: $–2xyz;\sqrt{10}{x}^{2}y{z}^3;\frac{3}{4}$.

Đơn thức 3x²yz . 7yz không phải là đơn thức thu gọn vì trong tích 3x²yz . 7yz có hai số là 3 và 7; các biến y, z xuất hiện hai lần.

Thu gọn đơn thức:

3x²yz . 7yz = (3 . 7)x² (y . y)(z . z) = 21x²y²z².

Chú ý:

• Để thu gọn một đơn thức, ta nhóm các thừa số là các số rồi tính tích của chúng, nhóm các thừa số cùng một biến rồi viết tích của chúng thành lũy thừa của biến đó.

• Từ nay, khi nói đến đơn thức, nếu không nói gì thêm, ta hiểu đó là đơn thức thu gọn.

3. Cộng, trừ đơn thức đồng dạng

– Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.

– Để cộng, trừ (hay tìm tổng, hiệu) hai đơn thức đồng dạng, ta cộng, trừ hệ số của chúng và giữ nguyên phần biến.

Ví dụ 4.Mỗi cặp đơn thức sau có đồng dạng không? Nếu có, hãy tìm tổng và hiệu của chúng.

a) 2xy² và 2x²y.

b) 3xy và – xy.

Hướng dẫn giải

a) 2xy² và 2x²y không phải là hai đơn thức đồng dạng vì phần biến xy² và x²y là khác nhau.

b) 3xy và – xy là hai đơn thức đồng dạng vì có hệ số khác 0 và cùng phần biến là xy.

Ta có

3xy + (– xy) = (3 – 1)xy = 2xy.

3xy – (– xy) = (3 + 1)xy = 4xy.

4. Đa thức thu gọn

Đa thức thu gọn là đa thức không chứa hai hạng tử nào đồng dạng.

Chú ý:

• Biến đổi một đa thức thành đa thức thu gọn gọi là thu gọn đa thức đó.

• Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng đó với nhau.

• Bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức gọi là bậc của đa thức đó.

Ví dụ 5.Thu gọn và tìm bậc của mỗi đa thức sau:

a) A = 2xy² + 3x²y + xy – xy² + x³.

b) B = x + y + 3xz – yz + 15y – x²z + 6yz.

Hướng dẫn giải

a) Ta có

A = 2xy² + 3x²y + xy – xy² + x³

= (2xy² – xy²) + 3x²y + xy + x³

= xy² + 3x²y + xy + x³

Các hạng tử của A lần lượt có bậc là 3; 3; 2; 3.

Do đó bậc của A bằng 3.

b) Ta có

B = x + y + 3xz – yz + 15y – x²z + 6yz

= x + (y + 15y) + 3xz – (yz – 6yz) – x²z

= x + 16y + 3xz + 5yz – x²z

Các hạng tử của B lần lượt có bậc là 1; 1; 2; 2; 3.

Do đó bậc của B bằng 3.

B. Bài tập tự luyện

Bài 1.Chỉ ra các đơn thức, đa thức trong các biểu thức sau:

$1+\frac{x}{y};2-x;3\text{x}yz;5\sqrt{x};x^{2}y;\frac{1}{3}+x^2+y.$

Hướng dẫn giải

Các đơn thức là: 3xyz; x²y.

Các đa thức gồm:

+ Các đơn thức 3xyz; x²y;

+ Đa thức $\frac{1}{3}+x^2+y$ và 2 – x.

Bài 2.Thu gọn các đơn thức sau, chỉ ra phần biến, hệ số của mỗi đơn thức đó.

$\frac{1}{3}x\frac{2}{3}y\frac{4}{3}x\text{z;}–5a^{3}b3cb.$

Hướng dẫn giải

•Ta có

Đơn thức trên có hệ số là , bậc bằng 2 + 1 + 1 = 4;

•Ta có – 5a³b3cb = (–5 . 3)a³(b . b)c = – 15a³b²c

Đơn thức trên có hệ số là –15, bậc bằng 3 + 2 + 1 = 6.

Bài 3.Thu gọn và tìm bậc của mỗi đa thức:

a) A = 2x⁵y + 7xy² – x⁵ + x⁵y – 10.

b) B = x²y² – 3xy² + 2x²y² + 5x²y.

Hướng dẫn giải

a) A = 2x⁵y + 7xy² – x⁵ + x⁵y – 10

= (2x⁵y + x⁵y) + 7xy² – x⁵ – 10

= 3x⁵y + 7xy² – x⁵ – 10

Các hạng tử của A lần lượt có bậc là 6; 3; 5; 0

Do đó bậc của A bằng 6.

b) B = x²y² – 3xy² + 2x²y² + 5x²y

= (x²y² + 2x²y²) – 3xy² + 5x²y

= 3x²y² – 3xy² + 5x²y

Các hạng tử của B lần lượt có bậc là 4; 3; 3

Do đó bậc của A bằng 4.

Bài 4.Tính giá trị của biểu thức A = x – y + z + y³ + x²y – z⁵ tại x = 5, y = 2, z = –1.

Hướng dẫn giải

Thay x = 5, y = 2, z = – 1 vào đa thức A = x – y + z + y³ + x²y – z⁵ ta được

A = 5 – 2 + (–1) + 2³ + 5² . 2 – (–1)⁵

= 5 – 2 – 1 + 8 + 25 . 2 + 1

= 61

Vậy A = 61.

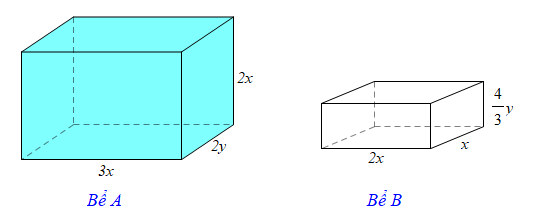
Bài 5. Có hai bể hình hộp chữ nhật A (đầy nước) và B (bể rỗng) có các kích thước (đơn vị: mét) như hình vẽ.

a) Viết biểu thức biểu thị phần nước còn lại ở bể A sau khi đổ nước từ bể A sang bể B (coi phần nước bị đổ ra ngoài khi đổ từ bể A sang bể B không đáng kể).

b) Khi x = 0,2 (m) và y = 0,5 (m) thì trong bể A còn lại khoảng bao nhiêu lít nước (làm tròn kết quả đến hàng phần mười)?

Hướng dẫn giải

a) Thể tích bể A là:

3x . 2y . 2x = (3 . 2 . 2)(x . x)y = 12x²y (m³).

Thể tích bể B là:

Phần nước còn lại ở bể A sau khi đổ nước từ bể A sang bể B là:

$12{\text{x}}^{2}y-\frac{8}{3}{\text{x}}^{2}y=\frac{28}{3}{\text{x}}^{2}y$ (m³).

b) Thay x = 0,2 (m) và y = 0,5 (m) vào biểu thức $\frac{28}{3}{\text{x}}^{2}y$ta được:

Vậy trong bể A còn lại khoảng 186,7 lít nước.