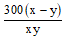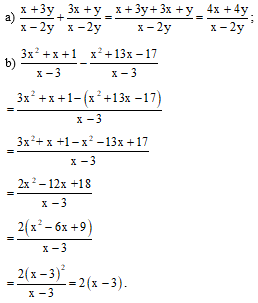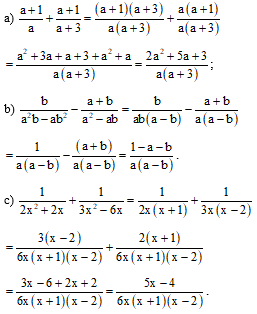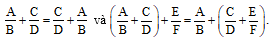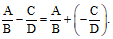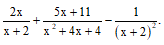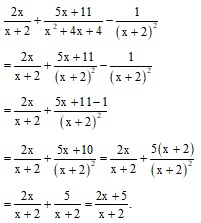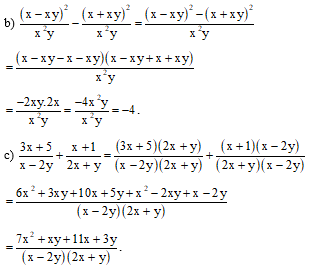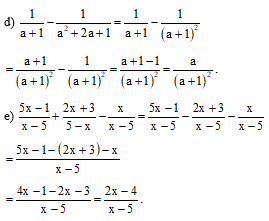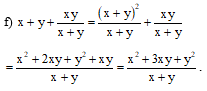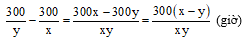Lý thuyết Toán 8 Chân trời sáng tạo Bài 6: Cộng, trừ phân thức

---

Haylamdo biên soạn và sưu tầm tóm tắt lý thuyết Toán 8 Bài 6: Cộng, trừ phân thức sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Lý thuyết Toán 8 Chân trời sáng tạo Bài 6: Cộng, trừ phân thức

A. Lý thuyết

1. Cộng, trừ hai phân thức cùng mẫu

Muốn cộng (hoặc trừ) hai phân thức có cùng mẫu thức, ta cộng (hoặc trừ) các tử thức với nhau và giữ nguyên mẫu thức.

$\frac{A}{B}+\frac{C}{B}=\frac{A+C}{B};\frac{A}{B}-\frac{C}{B}=\frac{A-C}{B}.$

Chú ý: Phép cộng phân thức có các tính chất giao hoán, kết hợp tương tự như đối với phân số.

Ví dụ 1. Thực hiện các phép tính cộng, trừ phân thức sau:

a) $\frac{x+3y}{x-2y}+\frac{3\text{x}+y}{x-2y}$;

b) $\frac{3{\text{x}}^2+x+1}{x-3}-\frac{{\text{x}}^2+13x-19}{x-3}$.

Hướng dẫn giải.

2. Cộng, trừ hai phân thức khác mẫu

Nhận xét:

• Quy đồng mẫu thức hai phân thức là biến đổi hai phân thức đã cho thành hai phân thức mới có cùng mẫu thức và lần lượt bằng hai phân thức đã cho.

•Mẫu thức của hai phân thức mới đó gọi là mẫu thức chung của hai phân thức đã cho.

Cộng, trừ hai phân thức khác mẫu

Muốn cộng, trừ hai phân thức khác mẫu thức, ta thực hiện các bước:

+ Quy đồng mẫu thức:

+ Cộng, trừ các phân thức có cùng mẫu vừa tìm được.

Chú ý: Cho hai phân thức $\frac{A}{B}$ và $\frac{C}{D}$ .

• Ta có $\frac{A}{B}=\frac{A.D}{B.D}$ và $\frac{C}{D}=\frac{C.B}{D.B}$.

• Nếu D là một nhân tử của B (B = D . P với P là một đa thức) thì lấy mẫu thức chung là B. Khi đó, ta quy đồng mẫu thức:

$\frac{C}{D}=\frac{C.\text{P}}{D.\text{P}}=\frac{C.\text{P}}{B}$ (giữ nguyên phân thức $\frac{A}{B}$).

(Tương tự cho trường hợp B là một nhân tử của D).

• Nếu B và D có nhân tử chung là E (B = E . M, D = E . N với M và N là những đa thức) thì lấy mẫu thức chung là E . M . N. Khi đó, ta quy đồng mẫu thức:

$\frac{A}{B}=\frac{A.\text{N}}{B.\text{N}}=\frac{A.N}{E.M.N}$ và $\frac{C}{D}=\frac{C.\text{M}}{D.\text{M}}=\frac{C.\text{M}}{\text{E}.\text{N . M}}=\frac{C.\text{M}}{\text{E}.\text{M . N}}$

Ví dụ 2. Thực hiện các phép cộng, trừ phân thức sau:

a) $\frac{a+1}{a}+\frac{a+1}{a+3}$;

b) $\frac{b}{a^{2}b-a{b}^2}-\frac{a+b}{a^2-ab}$.

c) $\frac{1}{2x^2+2x}+\frac{1}{3x^2-6x}$.

Hướng dẫn giải.

Chú ý:

• Phép cộng các phân thức cũng có tính chất giao hoán, kết hợp:

Nhờ tính chất kết hợp, trong một dãy phép cộng nhiều phân thức, ta không cần đặt dấu ngoặc.

•Hai phân thức đối nhau khi tổng của chúng bằng 0.

Phân thức đối của $\frac{A}{B}$ kí hiệu là $-\frac{A}{B}$. Tương tự như với phân số, ta có tính chất:

$-\frac{A}{B}=\frac{-A}{B}=\frac{A}{-B}.$

• Phép trừ phân thức có thể chuyển thành phép cộng với phân thức đối:

Ví dụ 4: Thực hiện phép tính

Hướng dẫn giải.

B. Bài tập tự luyện

Bài 1.Thực hiện các phép cộng, trừ phân thức sau:

a) $\frac{2\text{x}+1}{x+y}+\frac{2y+1}{y+x}$;

b) $\frac{{\left(x-xy\right)}^2}{x^{2}y}-\frac{{\left(x+xy\right)}^2}{x^{2}y}$.

c) $\frac{3\text{x}+5}{x-2y}+\frac{x+1}{2\text{x}+y}$;

d) $\frac{1}{a+1}-\frac{1}{a^2+2\text{a}+1}$.

e) $\frac{5\text{x}-1}{x-5}+\frac{2\text{x}+3}{5-x}-\frac{x}{x-5}$;

f) $\text{x}+y+\frac{xy}{x+y}$.

Hướng dẫn giải

a) $\frac{2\text{x}+1}{x+y}+\frac{2y+1}{y+x}=\frac{2\text{x}+1}{x+y}+\frac{2y+1}{x+y}=\frac{2\text{x}+1+2y+1}{x+y}=\frac{2\text{x}+2y+2}{x+y}$.

Bài 2.Hai ô tô cùng đi từ thành phố A đến thành phố B cách nhau 300 km, biết vận tốc ô tô thứ nhất là x (km/h), vận tốc ô tô thứ nhất là y (km/h) (x > y). Nếu xuất phát cùng lúc thì ô tô nào đến trước và đến trước bao nhiêu giờ?

Hướng dẫn giải

Thời gian ô tô thứ nhất đi từ A đến B là $\frac{300}{x}$ (giờ)

Thời gian ô tô thứ hai đi từ A đến B là $\frac{300}{y}$ (giờ)

Vì x > y nên $\frac{300}{x}<\frac{300}{y}$

Suy ra ô tô thứ nhất sẽ đến B trước ô tô thứ hai.

Thời gian ô tô thứ nhất đến trước ô tô thứ hai là:

Vậy ô tô thứ nhất đến trước ô tô thứ hai và đến trước giờ.