Lý thuyết Toán 8 Chân trời sáng tạo Bài 3: Hình thang – Hình thang cân

---

Haylamdo biên soạn và sưu tầm tóm tắt lý thuyết Toán 8 Bài 3: Hình thang – Hình thang cân sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 8 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 8.

Lý thuyết Toán 8 Chân trời sáng tạo Bài 3: Hình thang – Hình thang cân

A. Lý thuyết

1. Hình thang – Hình thang cân

Định nghĩa:

– Hình thang là tứ giác có hai cạnh đối song song.

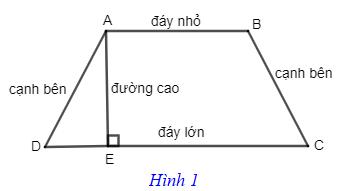
Hình 1là hình thang ABCD với AB // CD. Ta có:

+ Các đoạn thẳng AB, CD gọi là các cạnh đáy (hoặc đáy).

Nếu AB < CD thì AB gọi là đáy nhỏ, CD gọi là đáy lớn.

+ Các đoạn thẳng AD, BC gọi là các cạnh bên.

+ AE là đường vuông góc kẻ từ E đến đường thẳng CD, đoạn thẳng AE gọi là đường cao của hình thang ABCD.

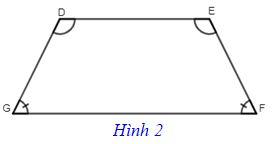
– Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

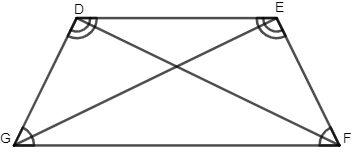
Hình 2 là hình thang cân DEFG với hai đáy là DE và FG có ; .

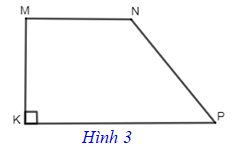
–Hình thang có một góc vuông được gọi là hình thang vuông.

Hình 3 là hình thang vuông MNPK với hai đáy là MN và KP có $\hat{K}=90°$ .

Ví dụ 1. Tìm các góc chưa biết của hình thang ABCD có hai đáy là AB và CD trong các trường hợp sau:

a) $\hat{C}=\hat{D}=60°$;

b) $\hat{A}=90°$và $\hat{B}=50°$.

Hướng dẫn giải

ABCD là hình thang có hai đáy là AB và CD nên AB // CD.

a) Vì $\hat{C}=\hat{D}=60°$nên hình thang ABCD là hình thang cân.

Áp dụng định lí tổng các góc của một tứ giác, ta có: $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$

Do đó: $\hat{A}+\hat{B}=360°-\left(\hat{C}+\hat{D}\right)={360}^{\circ }-(60°+60°)=360°-120°=240°$

Suy ra $\hat{A}=\hat{B}=\frac{240°}{2}=120°$.

b) $\hat{A}=90°$ nên hình thang ABCD là hình thang vuông, suy ra $\hat{A}=\hat{D}=90°$

Áp dụng định lí tổng các góc của một tứ giác, ta có:

$\hat{C}={360}^{\circ }-\left(\hat{A}+\hat{B}+\hat{D}\right)$

Do đó $\hat{C}=360°-\left(90°+50°+90°\right)=360°-230°=130°$

2. Tính chất của hình thang cân

Tính chất của hình thang cân:

Trong hình thang cân:

– Hai cạnh bên bằng nhau.

– Hai đường chéo bằng nhau.

Chú ý:Nếu một hình thang là hình thang cân thì nó có hai cạnh bên bằng nhau, nhưng một hình thang có hai cạnh bên bằng nhau thì chưa chắc là hình thang cân.

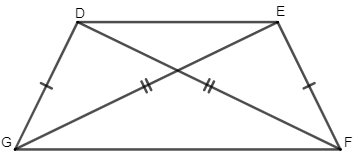
Ví dụ 2. Cho hình thang DEFG, trong đó $\hat{D}=\hat{E}$ và $\hat{F}=\hat{G}$. Tìm các đoạn thẳng bằng nhau trong hình thang DEFG.

Hướng dẫn giải

Vì $\hat{D}=\hat{E}$ và $\hat{F}=\hat{G}$ nên hình thang DEFG là hình thang cân.

Trong hình thang cân thì:

– Hai cạnh bên bằng nhau nên DG = EF;

– Hai đường chéo bằng nhau nên DF = EG.

3. Dấu hiệu nhận biết hình thang cân

– Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

– Hình thang có hai đường chéo bằng nhau là hình thang cân.

Ví dụ 3. Chứng minh mỗi hình thang dưới đây là hình thang cân.

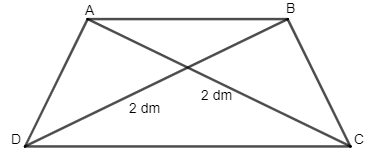
a) Hình thang ABCD có AC = BD = 2 dm.

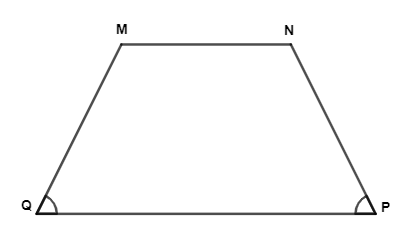
b) Hình thang MNPQ có $\widehat{MQP}=\widehat{NPQ}$.

Hướng dẫn giải

a) Hình thang ABCD có AC = BD = 2 dm, mà AC và BD là hai đường chéo của hình thang

Vì vậy hình thang ABCD là hình thang cân.

b) Hình thang MNPQ có $\widehat{MQP}=\widehat{NPQ}$mà $\widehat{MQP}$ và $\widehat{NPQ}$ là hai góc kề đáy QP của hình thang MNPQ.

Vì vậy hình thang MNPQ là hình thang cân.

B. Bài tập tự luyện

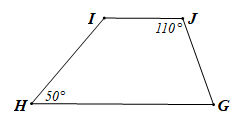
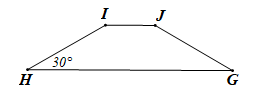
Bài 1. Tính số đo các góc chưa biết của hình thang IJGH (IJ // GH) trong các trường hợp sau:

a) $\hat{H}=50°$ , $\hat{J}=110°$ .

b) IJGH là hình thang cân và $\hat{H}=30°$ .

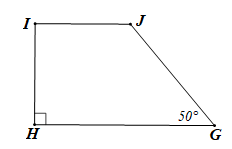
c) $\hat{H}=90°$ , $\hat{G}=50°$ .

Hướng dẫn giải

a)

Do IJ // GH nên ta có:

$\hat{I}+\hat{H}=180°$, suy ra $\hat{I}=180°-\hat{H}=180°-50°=130°$

$\hat{J}+\hat{G}=180°$, suy ra $\hat{G}=180°-\hat{J}=180°-110°=70°$

Vậy hình thang IJGH có: $\hat{I}=130°$; $\hat{G}=70°$.

b)

Hình thang cân IJGH (IJ // GH) có $\hat{I}=\hat{J}$ và $\hat{G}=\hat{H}=30°$ (tính chất hình thang cân).

Áp dụng định lí tổng các góc của một tứ giác, ta có:

$\hat{I}+\hat{J}+\hat{G}+\hat{H}=360°$

Suy ra $2\hat{I}=360°-2\hat{H}=360°-2.30°=300°$

Do đó $\hat{I}=\hat{J}=150°$ .

Vậy hình thang cân IJGH có: $\hat{G}=30°$; $\hat{I}=\hat{J}=150°$.

c)

$\hat{H}=90°$ nên hình thang IJGH là hình thang vuông, suy ra $\hat{H}=\hat{I}=90°$

Áp dụng định lí tổng các góc của một tứ giác, ta có:

$\hat{J}=360°-\left(\hat{I}+\hat{G}+\hat{H}\right)=360°-\left(90°+50°+90°\right)=360°-230°=130°$

Vậy hình thang vuông IJGH có: $\hat{I}=90°$ , $\hat{J}=130°$ .

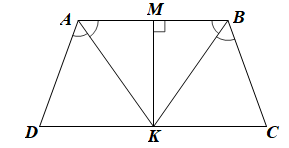
Bài 2. Cho hình thang cân ABCD (AB // CD). Hai tia phân giác của A và B cắt nhau tại điểm K nằm trên cạnh đáy DC. Từ K kẻ đoạn thẳng KM vuông góc với AB tại M.

a) Chứng minh ∆ABK là tam giác cân.

b) Chứng minh AM = BM.

Hướng dẫn giải

a) Do AK là tia phân giác của $\hat{A}$ nên $\widehat{DAK}=\widehat{KAB}=\frac{\widehat{DAB}}{2}$.

BK là tia phân giác của $\hat{B}$ nên $\widehat{CBK}=\widehat{KBA}=\frac{\widehat{CBA}}{2}$.

Mà ABCD là hình thang cân nên $\widehat{DAB}=\widehat{CBA}$ (tính chất hình thang cân).

Do đó $\widehat{KAB}=\widehat{KBA}$, suy ra ∆ABK là tam giác cân tại K.

b) Vì ∆ABK là tam giác cân nên KM là đường cao và cũng là đường trung tuyến ứng với cạnh đáy AB.

Do vậy M là trung điểm của AB nên AM = BM.

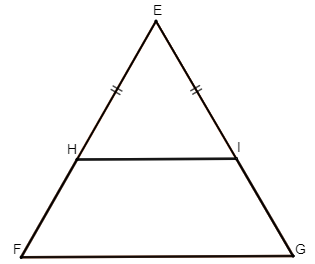
Bài 3. Cho tam giác cân EFG có EF = EG. Trên các cạnh EF và EG, lần lượt lấy các điểm H và I sao cho EH = EI.

a) Chứng minh HIGF là hình thang.

b) Chứng minh HIGF là hình thang cân.

Hướng dẫn giải

a) Ta có EH = EI nên ∆EHI là tam giác cân tại E.

Suy ra $\widehat{EHI}=\widehat{EIH}=\frac{180°-\hat{E}}{2}$ (1)

Lại có EF = EG nên ∆EFG là tam giác cân tại E.

Suy ra $\widehat{EFG}=\widehat{EGF}=\frac{180°-\hat{E}}{2}$ (2)

Từ (1) và (2) suy ra $\widehat{EHI}=\widehat{EFG}$.

Mà $\widehat{EHI}$ và $\widehat{EFG}$ ở vị trí đồng vị nên HI // FG (dấu hiệu nhận biết).

Suy ra tứ giác HIGF là hình thang.

b) Vì ∆EFG là tam giác cân nên $\hat{F}=\hat{G}$.

Suy ra hình thang HIGF là hình thang cân.

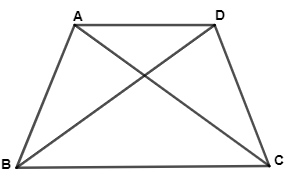
Bài 4. Cho hình thang ABCD (AD // BC) có AC = BD.

a) Hình thang ABCD là hình thang gì? Vì sao?

b) Chứng minh $\widehat{ADB}=\widehat{DAC}$ .

Hướng dẫn giải

a) Vì hai đường chéo của hình thang ABCD là AC và BD bằng nhau nên hình thang ABCD là hình thang cân.

b) Theo tính chất hình thang cân, ta có: AB = DC

Xét ∆ABD và ∆DCA có:

AD là cạnh chung;

AB = DC;

BD = AC.

Suy ra ∆ABD = ∆DCA (c.c.c)

Do đó $\widehat{ADB}=\widehat{DAC}$ (hai cạnh tương ứng).