Luyện tập 2 trang 87 Toán 8 Tập 2 | Kết nối tri thức Giải Toán 8

Giải Toán 8 Bài 34: Ba trường hợp đồng dạng của hai tam giác - Kết nối tri thức

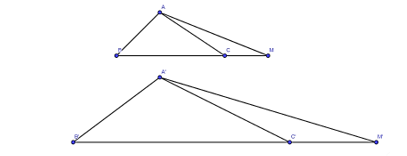
Luyện tập 2 trang 87 Toán 8 Tập 2: Cho ΔA'B'C' ∽ ΔABC. Trên tia đối của các tia CB, C'B' lần lượt lấy các điểm M, M' sao cho $\frac{M C}{M B} = \frac{M' C'}{M' B'}$ . Chứng minh rằng ΔA'B'M' ∽ ΔABM.

Lời giải:

Luyện tập 2 trang 87 Toán 8 Tập 2 | Kết nối tri thức Giải Toán

Có $\frac{M C}{M B} = \frac{M' C'}{M' B'}$ . Suy ra $\frac{M B - B C}{M B} = \frac{M' B' - B' C'}{M' B'}$

Suy ra $1 - \frac{B C}{M B} = 1 - \frac{B' C'}{M' B'}$ . Do đó, $\frac{B C}{M B} = \frac{B' C'}{M' B'}$ , suy ra $\frac{B' C'}{B C} = \frac{M' B'}{M B}$ . (1)

Vì ΔA′B′C′ ∽ ΔABC. Suy ra $\hat{B} = \hat{B'}$ và $\frac{A' B'}{A B} = \frac{B' C'}{B C}$ . (2)

Từ (1) và (2) suy ra $\frac{M' B'}{M B} = \frac{A' B'}{A B}$ .

Xét tam giác ABM và tam giác A'B'M' có:

$\frac{M' B'}{M B} = \frac{A' B'}{A B}$ và $\hat{B} = \hat{B'}$ (chứng minh trên).

Do đó ΔABM ∽ ΔA′B′M′ (c.g.c).

Lời giải bài tập Toán 8 Bài 34: Ba trường hợp đồng dạng của hai tam giác hay, chi tiết khác:

Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯