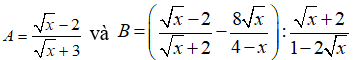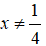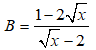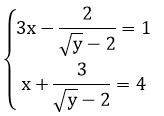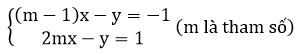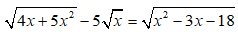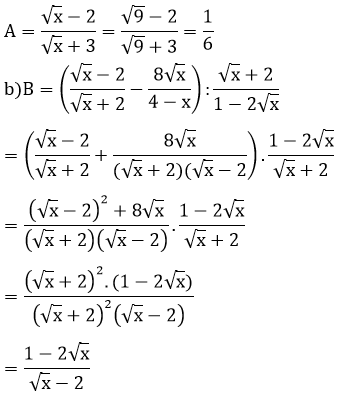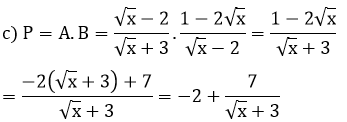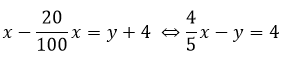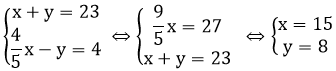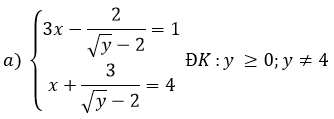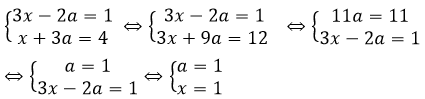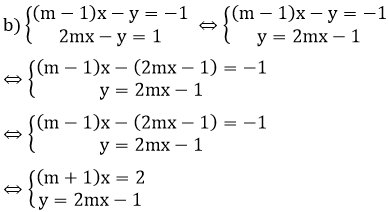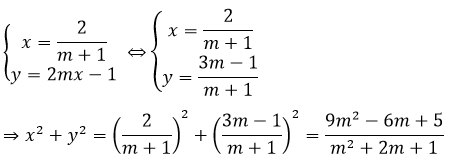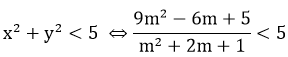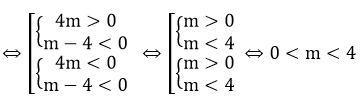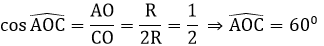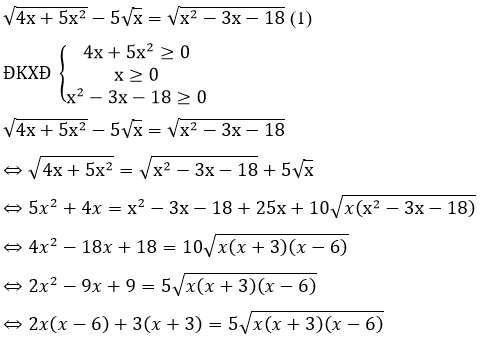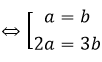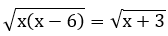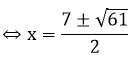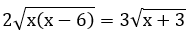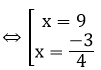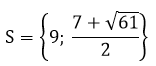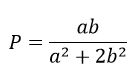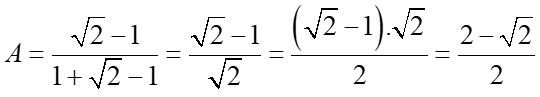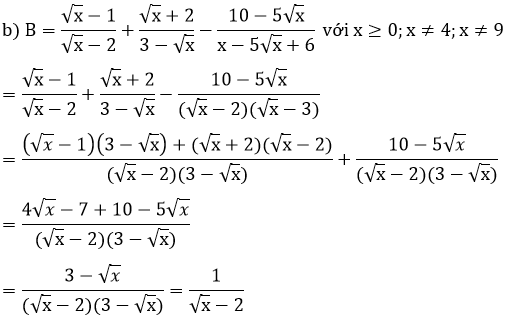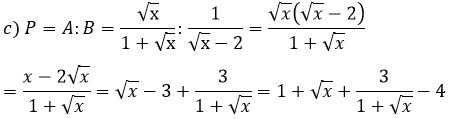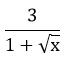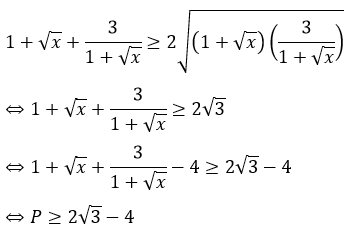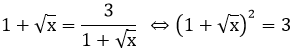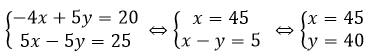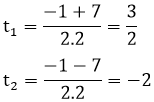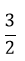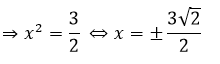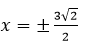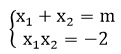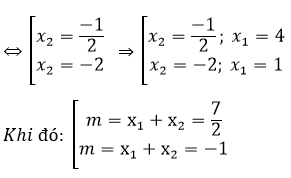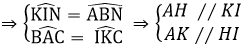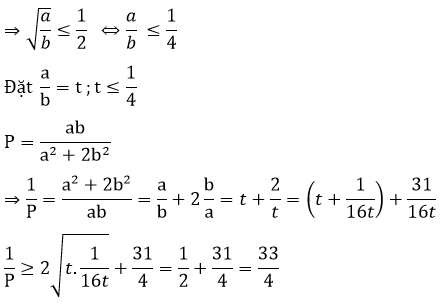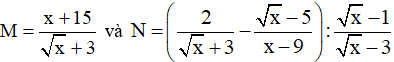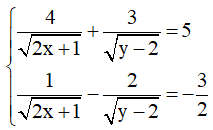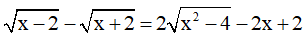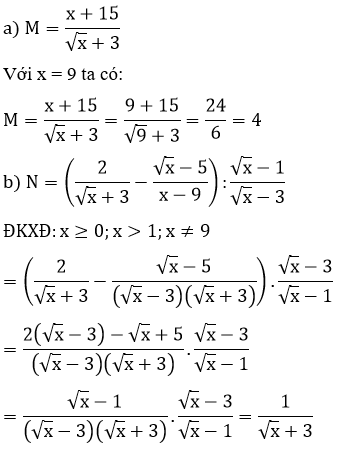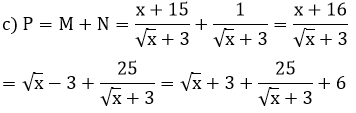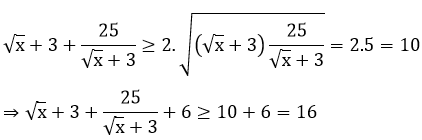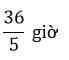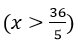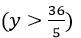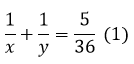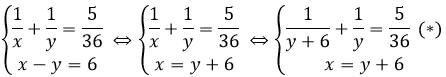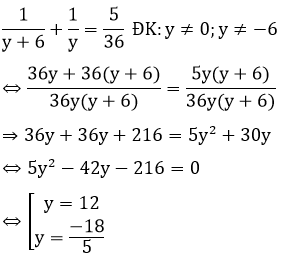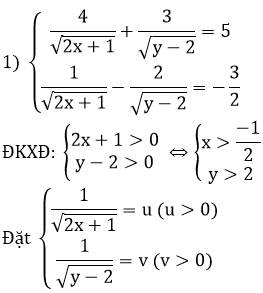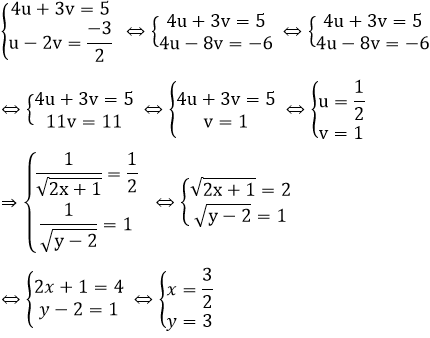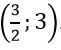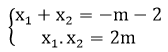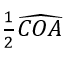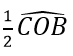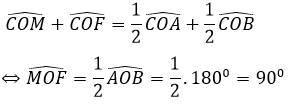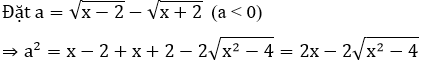Bộ đề thi vào lớp 10 môn Toán Tp. Hà Nội năm 2023 có đáp án

---

Bộ đề thi vào lớp 10 môn Toán Tp. Hà Nội năm 2023 có đáp án

Haylamdo biên soạn và sưu tầm Bộ đề thi vào lớp 10 môn Toán Tp. Hà Nội năm 2023 có đáp án được các Thầy/Cô giáo nhiều năm kinh nghiệm biên soạn và tổng hợp chọn lọc từ đề thi môn Toán vào lớp 10 của các trường THPT trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong kì thi tuyển sinh vào lớp 10 môn Toán.

Sở Giáo dục và Đào tạo .....

Trường THPT ....

Kì thi tuyển sinh vào lớp 10

Năm học 2023

Môn: Toán

Thời gian làm bài: 120 phút

(Đề thi số 1)

Bài 1: (2 điểm) Cho biểu thức:

Với x ≥ 0, x ≠ 4,

a. Tính giá trị của A khi x = 9

b. Chứng minh

c. Tìm giá trị lớn nhất của biểu thức P = A.B

Bài 2: (2 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:

Một mảnh đất hình chữ nhật có chu vi bằng 46m. Nếu tăng chiều rộng thêm 4m và giảm chiều dài đi 20% chiều dài ban đầu thì mảnh đất đó trở thành hình vuông. Tính diện tích của mảnh vườn hình chữ nhật đó.

Bài 3: (2 điểm)

a) Giải hệ phương trình

b) Cho hệ phương trình:

Tìm m để hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x² + y² < 5.

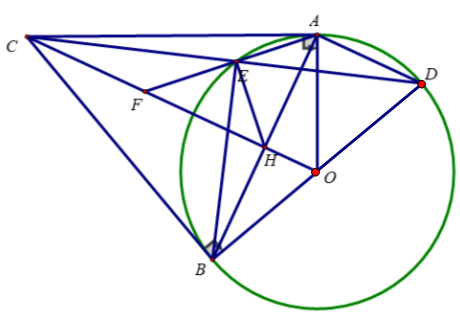
Bài 4: (3,5 điểm) Cho điểm C nằm ngoài đường tròn (O), kẻ hai tiếp tuyến CA, CB với đường tròn (O) (A, B là tiếp điểm).

a) Chứng minh 4 điểm C, A, O, B cùng thuộc một đường tròn

b) Vẽ dây AD // CO. CD cắt (O) tại E. Gọi giao điểm AE với CO là F. Chứng minh ECF = CAF và CF² = FE.FA

c) AB cắt CO tại H. Chứng minh ∠HEB = ∠CEF

d) Khi OC = 2R. Tính FO theo R.

Bài 5: (0,5 điểm) Giải phương trình sau:

Đáp án và Hướng dẫn giải

Bài 1:

a) Khi x =9 ta có:

Biểu thức P đạt GTLN khi và chỉ khi:

đạt GTLN ⇔ √x + 3 đạt GTNN

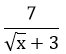
⇔ √x = 0 ⇔ x = 0

Khi đó GTLN của P là:

Vậy GTLN của P là 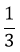đạt được khi x = 0

Bài 2:

Gọi chiều dài của hình chữ nhật là x (m) (0 < x < 23)

Gọi chiều rộng của hình chữ nhật là y (m) (0 < y < x < 23)

Chu vi hình chữ nhật là 46 m nên ta có phương trình

2(x + y) = 46 ⇔ x + y = 23

Nếu tăng chiều rộng 4m và giảm chiều dài đi 20% thì mảnh đất đó trở thành hình vuông nên ta có phương trình

Ta có hệ phương trình:

Vậy chiều dài của hình chữ nhật là 15m

Chiều rộng của hình chữ nhật là 8m

Bài 3:

Đặt 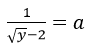(a ≠ 0), hệ phương trình trở thành:

Với a = 1, ta có:

⇔ √y - 2 = 1 ⇔ √y = 3 ⇔ y = 9

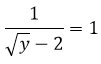
Vậy hệ phương trình có nghiệm (x; y) = (1; 9)

Hệ phương trình có nghiệm duy nhất khi và chỉ khi m + 1 ≠ 0 ⇔ m ≠ -1

Khi đó:

Theo bài ra:

⇔ 9m² - 6m + 5 < 5m² + 10m + 5

⇔ 4m² - 16m < 0

⇔ 4m(m - 4) < 0

Đối chiếu điều kiện, m ≠ -1 thỏa mãn

Vậy với 0 < m < 4 thì thỏa mãn yêu cầu đề bài.

Bài 4:

a) Xét tứ giác CAOB có:

∠CAO = 90^o (AC là tiếp tuyến của (O))

∠CBO = 90^o (BC là tiếp tuyến của (O))

=> ∠CAO + ∠CBO = 180^o

=> Tứ giác BCAO là tứ giác nội tiếp

b) Xét đường tròn (O) có:

∠CAF = ∠ADE (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn 1 cung)

Lại có: ∠ECF = ∠ADE (CO // AD; hai góc so le trong)

=> ∠CAF = ∠ECF

Xét ΔCFA và ΔEFC có:

∠CAF = ∠ECF

∠CFA là góc chung

=> ΔCFA ∼ ΔEFC

=> CF² = FE.FA

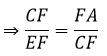
c) Ta có:

∠CAF = ∠EBA (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn 1 cung)

Lại có: ∠CAF = ∠ECF (cmt)

=> ∠EBA = ∠ECF

Xét tứ giác CEBH có:

∠EBA = ∠ECF

=> 2 đỉnh B và C cùng nhìn EH dưới 2 góc bằng nhau

=> Tứ giác CEBH là tứ giác nội tiếp

=> ∠BEH = ∠HCB ( 2 góc nội tiếp cùng chắn cung HB)

Mà ∠HCB = ∠HCA (CO là tia phân giác của góc ACB)

=> ∠BEH = ∠HCA (1)

Mặt khác: ΔCFA ∼ ΔEFC => ∠HCA = ∠CEF (2 góc tương ứng) (2)

Từ (1) và (2) : ∠BEH = ∠CEF

d) Xét tam giác ACO vuông tại A có:

AC² + AO² = CO² => AC² = 4R² - R² = 3R²

=> CB² = CA² = 3R²

Ta có: AB ⊥ CO (Tính chất 2 tiếp tuyến cắt nhau)

CO // AD (gt)

=> AB ⊥ AD => BD là đường kính của đường tròn (O)

Xét tam giác BCD vuông tại B có:

BC² + BD² = CD² => CD² = 3R² + 4R² = 7R²

=> CD = R√7

Xét ΔCEA và ΔCDA có:

Xét tam giác CAO vuông tại A có:

=> ∠BOA = 2∠AOC = 120^o => ∠AOD = 60^o (kề bù với góc (BOA )

Tam giác AOD cân tại O có ∠AOD = 60^o nên tam giác AOD đều

=> AD = AO = R

Ta có: OC // AD

Bài 5:

Đặt 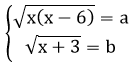(a,b ≥ 0),phương trình trở thành:

2a² + 3b² = 5ab

⇔ 2a² -2ab + 3b² - 3ab = 0

⇔ (a - b)(2a - 3b) = 0

Với a = b, ta có:

⇔ x² - 6x = x + 3

⇔ x² - 7x - 3 = 0

Với 2a = 3b, ta có:

⇔ 4x² - 24x = 9x + 27

⇔ 4x² - 33x - 27 = 0

Đối chiếu với ĐKXĐ thì phương trình có tập nghiệm là

Sở Giáo dục và Đào tạo .....

Trường THPT ....

Kì thi tuyển sinh vào lớp 10

Năm học 2023

Môn: Toán

Thời gian làm bài: 120 phút

(Đề thi số 2)

Bài 1: (2 điểm) Cho biểu thức:

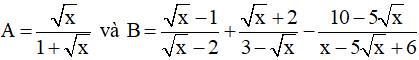
với x ≥ 0, x ≠ 9, x ≠ 4

a) Tính giá trị biểu thức A khi x = 3 - 2√2

b) Rút gọn biểu thức B

c) Tìm giá trị nhỏ nhất của biểu thức P = A : B

Bài 2: (2 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình

Theo kế hoạch, một tổ công nhân phải làm một số sản phẩm trong một thời gian nhất định. Nếu mỗi ngày họ làm tăng thêm 5 sản phẩm so với dự định thì sẽ hoàn thành kế hoạch trước thời hạn 4 ngày. Nếu mỗi ngày họ làm ít hơn 5 sản phẩm so với dự định thì sẽ hoàn thành kế hoạch châm hơn thời hạn 5 ngày. Tính thời gian và số sản phẩm phải làm theo kế hoạch.

Bài 3: (2 điểm)

1) Giải phương trình 2x⁴ + x² - 6 = 0

2) Cho parabol (P): y = x² và đường thẳng (d): y = mx + 2

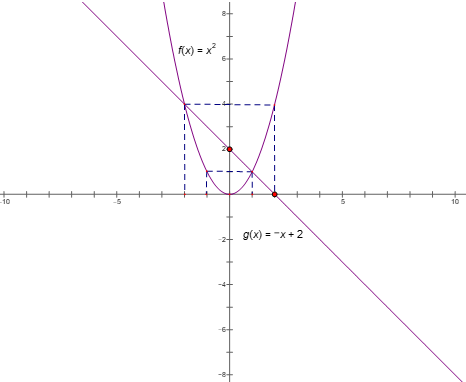
a) Với m = -1 : vẽ parabol (P) và đường thẳng (d) trên cùng một hệ trục tọa độ. Tìm tọa độ các giao điểm của parabol (P) và đường thẳng (d).

b) Tìm các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x₁, x₂ sao cho x₁ - 2x₂ = 5

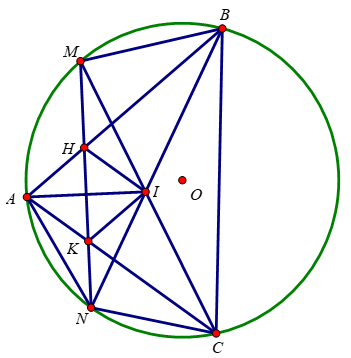
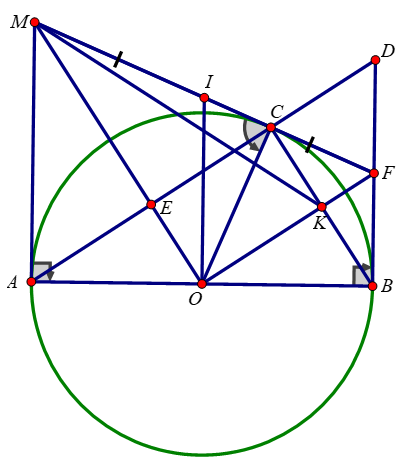
Bài 4: (3,5 điểm) Cho đường tròn tâm (O) với dây AB cố định không phải đường kính. Gọi C là điểm thuộc cung lớn AB sao cho tam giác ABC nhọn. M; N lần lượt là điểm chính giữa của cung nhỏ AB; AC. Gọi I là giao điểm của BN và CM. Dây MN cắt AB và AC lần lượt tại H và K.

a) Chứng minh tứ giác BMHI nội tiếp

b) Chứng minh MK.MN = MI.MC

c) Chứng minh tứ giác AKI cân tại K và tứ giác AHIK là hình thoi.

Bài 5: (0,5 điểm) Cho a, b là 2 số thực dương thỏa mãn điều kiện ab + 4 ≤ 2b. Tìm giá trị lớn nhất của biểu thức:

Đáp án và Hướng dẫn giải

Bài 1:

a) Ta có x = 3 - 2√2 = 2 - 2√2.1 + 1 = (√2 - 1)²

⇒ √x = √(√2 - 1)² = |√2 - 1| = √2 - 1 (vì √2 > 1)

Thay √x = √2 - 1 vào biểu thức A ta được:

Áp dụng Bất đẳng thức Cosi cho 2 số dương 1 + √x và

Dấu bằng xảy ra khi:

⇔ 1 + √x = √3 (do 1 + √x > 0)

⇔ √x = √3 - 1 ⇔ x = 4 - 2√3

Vậy GTNN của P là 2√3 - 4 đạt được khi x = 4 - 2√3

Bài 2:

Gọi số sản phẩm cần làm theo dự định trong một ngày là x (sản phẩm/ ngày) ( x > 5)

Thời gian dự định làm là y (ngày) (y > 4)

=> Số sản phẩm cần làm là xy ( sản phẩm)

Nếu mỗi ngày họ làm tăng thêm 5 sản phẩm so với dự định thì sẽ hoàn thành kế hoạch trước thời hạn 4 ngày nên ta có phương trình:

(x + 5)(y - 4) = xy ⇔ -4x + 5y = 20 (1)

Nếu mỗi ngày họ làm ít hơn 5 sản phẩm so với dự định thì sẽ hoàn thành kế hoạch châm hơn thời hạn 5 ngày nên ta có phương trình:

(x - 5)(y + 5) = xy ⇔ 5x - 5y = 25 (2)

Từ (1) và (2) ta có hệ phương trình:

Khi đó số sản phẩm cần làm là: x.y = 45.40 = 1800 (sản phẩm)

Vậy số sản phẩm cần làm là 1800 sản phẩm

Số ngày dự định làm là 40 ngày.

Bài 3:

1) 2x⁴ + x² - 6 = 0

Đặt x² = t ( t ≥ 0), phương trình trở thành:

2t² + t - 6 = 0

Δ = 1-4.2.(-6) = 49

=> Phương trình có 2 nghiệm phân biệt

Do t ≥ 0 nên t =

Vậy phương trình đã cho có nghiệm

2) a) Với m = -1, (d): y = - x + 2

(P): y = x²

Bảng giá trị:

x	-2	-1	0	1	2
y = x2	4	1	0	1	4

Đồ thị (P): y = x² là 1 đường parabol nằm phía trên trục hoành, nhận trục Oy làm trục đối xứng và nhận điểm O (0;0) làm đỉnh

y = - x + 2

Bảng giá trị:

x	0	2
y = -x + 2	2	0

Phương trình hoành độ giao điểm của (P) và (d) là:

x² = -x + 2 ⇔ x² + x - 2 = 0

=> Phương trình có 2 nghiệm x = 1; x = - 2

Khi đó tọa độ giao điểm của (P) và (d) là (1; 1) và (-2; 4)

b) Phương trình hoành độ giao điểm của (P) và (d) là:

x² = mx + 2 ⇔ x² - mx - 2 = 0

Δ = m² - 4.(-2) = m² + 8 > 0 ∀m

=> Phương trình luôn có 2 nghiệm phân biệt với mọi m

Theo hệ thức Vi-et ta có:

Theo bài ra: x₁ - 2x₂ = 5 ⇔ x₁ = 2x₂ + 5

=> (2x₂ + 5) x₂ = -2 ⇔ 2x₂² + 5x₂ + 2 = 0

Vậy có 2 giá trị của m thỏa mãn điều kiện đề bài là m = -1 ;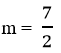

Bài 4:

a) Xét tứ giác HMBI có:

∠HMI = ∠HBI (2 góc nội tiếp chắn 2 cung bằng nhau )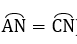

Mà 2 góc này cùng nhìn cạnh HI

=> Tứ giác BMHI nội tiếp

b) Xét ΔMNI và ΔMKC có:

∠KMC là góc chung

∠MNI = ∠KCM (2 góc nội tiếp chắn 2 cung bằng nhau )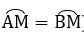

=> ΔMNI ∼ ΔMCK => 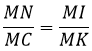=> MN.MK = MC.MI

c) Xét tứ giác NKIC có:

∠KNI = ∠KCI (2 góc nội tiếp chắn 2 cung bằng nhau )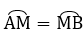

Mà 2 góc này cùng nhìn cạnh KI

=> Tứ giác NKIC là tứ giác nội tiếp

=> ∠NKI + ∠NCI = 180^o (1)

Xét đường tròn (O) có:

=> ∠ANK + ∠NAK = ∠ACM + ∠NCA = ∠NCI (2)

Xét tam giác AKN có: ∠ANK + ∠NAK + ∠NKA = 180^o (3)

Từ (1), (2), (3) => ∠NKI = ∠NKA

Xét tam giác IKN và tam giác AKN có:

∠NKI = ∠NKA

KN là cạnh chung

∠KNI = ∠KNA (2 góc nội tiếp chắn 2 cung bằng nhau)

=> ΔIKN = ΔAKN

=> IK=AK =>ΔAKI cân tại K

Tứ giác NKIC là tứ giác nội tiếp

Mặt khác ∠KCN = ∠ABN (2 góc nội tiếp cùng chắn cung AN của (O))

∠BAC = ∠BNC (2 góc nội tiếp cùng chắc cung BC của (O))

=> Tứ giác AHIK là hình bình hành

Mà IK = AK

=> Tứ giác AHIK là hình thoi.

Bài 5:

2b ≥ ab + 4 ≥ 4√ab ( Theo BDT Cosi)

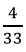
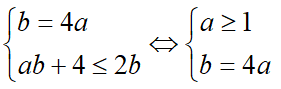
Vậy GTLN của P là khi .

Sở Giáo dục và Đào tạo .....

Trường THPT ....

Kì thi tuyển sinh vào lớp 10

Năm học 2023

Môn: Toán

Thời gian làm bài: 120 phút

(Đề thi số 3)

Bài 1: (2 điểm) Cho biểu thức

(ĐKXĐ: x ≥ 0; x ≠ 1; x ≠ 9 )

a) Tính giá trị của biểu thức M khi x = 9

b) Rút gọn biểu thức N

c) Tìm giá trị nhỏ nhất của biểu thức

Bài 2: (2 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình

Hai người cùng làm chung một công việc trong 7 giờ 12 phút thì xong công việc. Nếu mỗi người làm một mình thì người thứ nhất hoàn thành công việc chậm hơn người thứ hai là 6 giờ. Hỏi nếu làm một mình thì mỗi người phải làm trong bao lâu để hoàn thành công việc.

Bài 3: (2 điểm)

1) Giải hệ phương trình

2) Cho phương trình x² + (m + 2)x + 2m = 0 (*)

a) Chứng minh phương trình (*) luôn có hai nghiệm x₁, x₂ với mọi m

b) Tìm biểu thức liên hệ giữa x₁, x₂ không phụ thuộc vào m.

Bài 4: (3,5 điểm) Cho đường tròn (O; R), đường kính AB. Kẻ tiếp tuyến Ax với đường tròn tại A. Lấy điểm M thuộc tia Ax, kẻ tiếp tuyến MC với đường tròn (O) tại C (C khác A). Tiếp tuyến của đường tròn tại B cắt AC tại D và cắt MC tại F. Nối OM cắt AC tại E.

1) Chứng minh tứ giác OBDE nội tiếp

2) Chứng minh AC. AD = 4R²

3) Chứng minh AB là tiếp tuyến của đường tròn ngoại tiếp ΔMOF

Bài 5: (0,5 điểm) Giải phương trình:

Đáp án và Hướng dẫn giải

Bài 1:

Áp dụng Bất đẳng thức Cosi cho 2 số không âm √x + 3 và 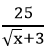ta được:

Dấu bằng xảy ra khi:

√x + 3 = 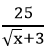⇔ (√x + 3)² = 25 ⇔ √x + 3 = 5 (do √x + 3 > 0)

⇔ √x = 2 ⇔ x = 4

Vậy GTNN của P = 16, đạt được khi x = 4

Bài 2:

Đổi 7 giờ 12 phút =

Gọi thời gian người thứ nhất làm một mình xong công việc là x (giờ)

Thời gian người thứ hai làm một mình xong công việc là y (giờ)

=> Trong 1 giờ, người thứ nhất làm được 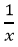công việc

Trong 1 giờ, người thứ nhất làm được 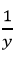công việc

Cả 2 người làm chung thì làm xong trong 7 giờ 12 phút nên ta có phương trình:

Người thứ nhất làm một mình hoàn thành công việc chậm hơn người thứ hai là 6 giờ nên ta có phương trình:

x - y = 6 (2)

Từ (1) và (2) ta có hệ phương trình

Giải phương trình (*):

Đối chiếu với ĐK thì y = 12 => x = y + 6 = 18

Vậy người thứ nhất làm 1 mình thì hoàn thành công việc trong 18 giờ

Người thứ hai làm 1 mình thì hoàn thành công việc trong 12 giờ.

Bài 3:

Khi đó hệ phương trình trở thành:

Vậy hệ phương trình đã cho có nghiệm duy nhất (x; y) =

2)x² + (m + 2)x + 2m = 0 (*)

a)Δ = (m + 2)² - 4.2m = m² + 4m + 4 - 8m = (m - 2)² ≥ 0 ∀m

=> phương trình (*) luôn có hai nghiệm x₁, x₂ với mọi m

b) Theo hệ thức Vi- ét, ta có:

=> 2(x₁ + x₂ ) + x₁.x₂ = -2(m + 2) + 2m = -4

Vậy 2(x₁ + x₂ ) + x₁.x₂ = -4 là hệ thức liên hệ giữa 2 nghiệm x₁, x₂ không phụ thuộc vào m

Bài 4:

a) M là giao điểm của 2 tiếp tuyến MC và MA

=> MO là đường trung trực của đoạn thẳng AC =>MO ⊥ AC

Xét tứ giác OBDE có:

∠OED = 90^o (MO ⊥ AC)

∠OBD = 90^o (BD là tiếp tuyến của (O))

=> ∠OED + ∠OBD = 180^o

=> Tứ giác OBDE là tứ giác nội tiếp

b) Xét tam giác ABD vuông tại D có BC là đường cao

Theo hệ thức lượng trong tam giác vuông: AC.AD = AB² = (2R)² = 4R²

Vậy AC.AD = 4R²

c) 2 tiếp tuyến MC và Ma cắt nhau tại M

=> OM là tia phân giác của ∠COA => ∠COM =

2 tiếp tuyến CF và FB cắt nhau tại F

=> OF là tia phân giác của ∠COB => ∠COF =

Khi đó:

Tam giác MOF vuông tại O

=> Tâm đường tròn ngoại tiếp tam giác MOF là trung điểm I của MF

Tam giác MIO cân tại I => ∠IOM = ∠IMO

Mặt khác ta có: ∠AMO = ∠IMO (do MO là tia phân giác ∠AMI )

=> ∠AMO = ∠IOM (1)

Tam giác MAO vuông tại A => ∠AMO + ∠AOM = 90^o(2)

Từ (1) và (2) => ∠IOM + ∠AOM =90^o ⇔ ∠AOI = 90^o hay AO ⊥ OI

=> AB là tiếp tuyến của đường tròn ngoại tiếp tam giác MOF

Bài 5:

ĐKXĐ: x ≥ 2

Khi đó, phương trình đã cho trở thành: a = - a² + 2

⇔ a² + a - 2 = 0

⇔ a = 1; a = -2

Do a < 0 nên a = - 2

Với a = -2, ta có:

Vậy phương trình có nghiệm x = 2