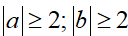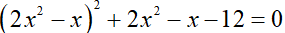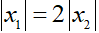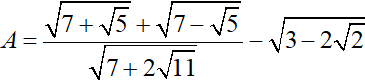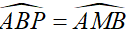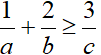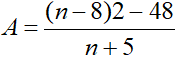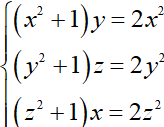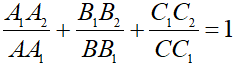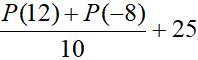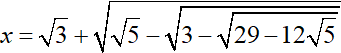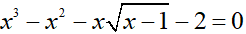Bộ đề thi vào lớp 10 chuyên Toán năm 2023 có đáp án

---

Bộ đề thi vào lớp 10 chuyên Toán năm 2023 có đáp án

Tải xuống

Haylamdo biên soạn và sưu tầm Bộ đề thi vào lớp 10 chuyên Toán năm 2023 có đáp án được các Thầy/Cô giáo nhiều năm kinh nghiệm biên soạn và tổng hợp chọn lọc từ đề thi môn Toán vào lớp 10 của các trường THPT trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong kì thi tuyển sinh vào lớp 10 môn Toán.

Sở Giáo dục và Đào tạo .....

Trường THPT ....

Kì thi tuyển sinh vào lớp 10

Năm học 2023

Môn: Toán (khối chuyên)

Thời gian làm bài: 120 phút

(Đề thi số 1)

Câu 1 (4 điểm):

a) Giải hệ phương trình: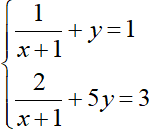

b) Giải phương trình:

Câu 2 (3 điểm):

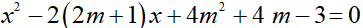
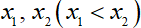
Cho phương trình: (x là ẩn số ). Tìm m để phương trình có hai nghiệm phân biệt thỏa mãn

Câu 3 (2 điểm):

Thu gọn biểu thức:

Câu 4 (4 điểm): Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Gọi P là điểm chính giữa của cung nhỏ AC. Hai đường thẳng AP và BC cắt nhau tại M. Chứng minh rằng:

a)

b) MA.MP=BA.BM

Câu 5 (3 điểm):

a) Cho phương trình 2x²+mx+2n+8=0 ( x là ẩn số và m, n là các số nguyên).Giả sử phương trình có các nghiệm đều là số nguyên. Chứng minh rằng m²+n² là hợp số.

b) Cho hai số dương a,b thỏa a¹⁰⁰+b¹⁰⁰=a¹⁰¹+b¹⁰¹=a¹⁰²+b¹⁰² . Tính a²⁰¹⁰+b²⁰¹⁰ .

Câu 6 (2 điểm): Cho tam giác OAB vuông cân tại O với OA=OB =2a. Gọi (O) là đường tròn tâm O bán kính a. Tìm điểm M thuộc (O) sao cho MA+2MB đạt giá trị nhỏ nhất

Câu 7 (2 điểm): Cho a,b là các số dương thỏa 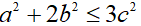. Chứng minh:

Sở Giáo dục và Đào tạo .....

Trường THPT ....

Kì thi tuyển sinh vào lớp 10

Năm học 2023

Môn: Toán (khối chuyên)

Thời gian làm bài: 120 phút

(Đề thi số 2)

Câu 1 (3 điểm):

a) Tìm các số nguyên dương n để

b) Tìm các số nguyên dương x, y thỏa mãn đẳng thức x²+y(y²+y-3x)=0

Câu 2 (2 điểm):

Giải hệ phương trình ( x,y,z là ẩn)

Câu 3 (3 điểm): Cho tam giác ABC có ba góc nhọn nội tiếp (O). Gọi BD và CE là hai đường cao của tam giác ABC.

a) Chứng minh AD.AC=AE.AB

b) Tia AO cắt BC tại A₁ và cắt cung nhỏ BC tại A₂. Tia BO cắt AC tại B₁ và cắt cung nhỏ AC tại B₂. Tia CO cắt BA tại C₁ và cắt cung nhỏ AB tại C₂. Chứng minh:

c) Từ A vẽ tia Ax vuông góc với DE. Cho cạnh BC cố định, đỉnh A di động trên cung lớn BC sao cho tam giác ABC có ba góc nhọn. Chứng minh tia Ax luôn đi qua một điểm cố định.

Câu 4 (1 điểm):

Cho đa thức P(x)=x⁴+ax³+bx²+cx+d (a,b,c,d là các hằng số)). Biết rằng P(1) = 10, P(2) = 20, P(3) = 30. Tính giá trị của biểu thức

Câu 5 (1 điểm):

Chứng minh rằng: Nếu ba điểm A, B, C không có điểm nào nằm bên ngoài đường tròn (O) sao cho tam giác ABC có ba góc nhọn thì chu vi của đường tròn ngoại tiếp tam giác ABC không lớn hơn chu vi (O).

Sở Giáo dục và Đào tạo .....

Trường THPT ....

Kì thi tuyển sinh vào lớp 10

Năm học 2023

Môn: Toán (khối chuyên)

Thời gian làm bài: 120 phút

(Đề thi số 3)

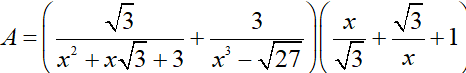
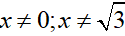
Câu 1 (2 điểm): Cho biểu thức: (với )

a) Rút gọn biểu thức A.

b) Tính giá trị của biểu thức A khi

Câu 2 (3 điểm):

a) Giải phương trình:

b) Giải hệ phương trình:

Câu 3 (1 điểm): Tìm các số tự nhiên n để A=n²⁰¹⁸+n²⁰⁰⁸+1 là số nguyên tố.

Câu 4 (3 điểm): Cho đường tròn (O; R), đường kính AB, M là một điểm tùy ý thuộc đường tròn (M khác A và B). Qua A và B lần lượt kẻ các đường thẳng d và d’ là tiếp tuyến với đường tròn. Tiếp tuyến tại M của đường tròn cắt d và d’ lần lượt tại C và D. Đường thẳng BM cắt d tại E.

a) Chứng minh CM = CA = CE.

b) Chứng minh AD⊥OE.

c) Tính độ dài đoạn AM theo R, nếu AE = BD.

Câu 5 (1 điểm): Cho a,b thoả mãn . Chứng minh rằng:

Tải xuống