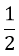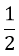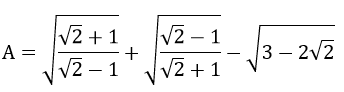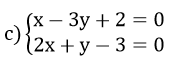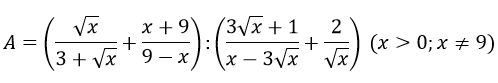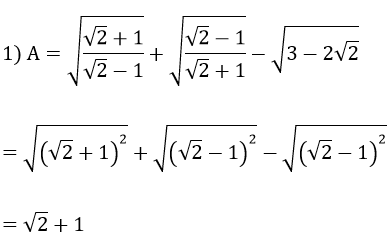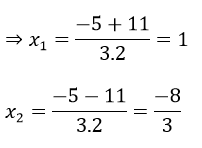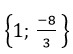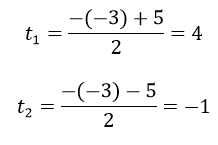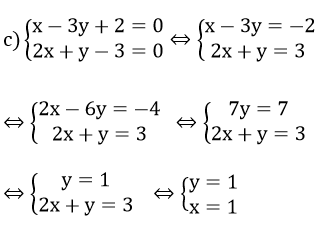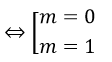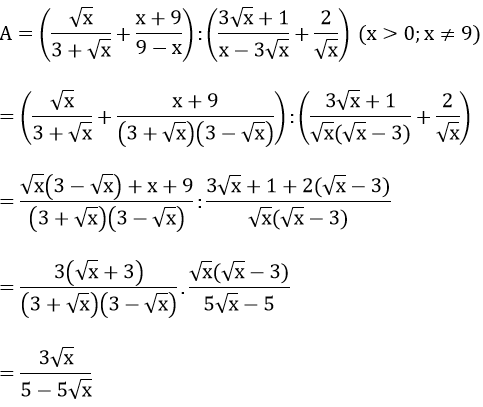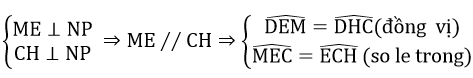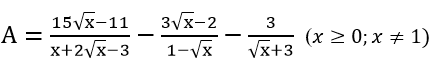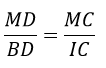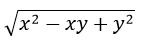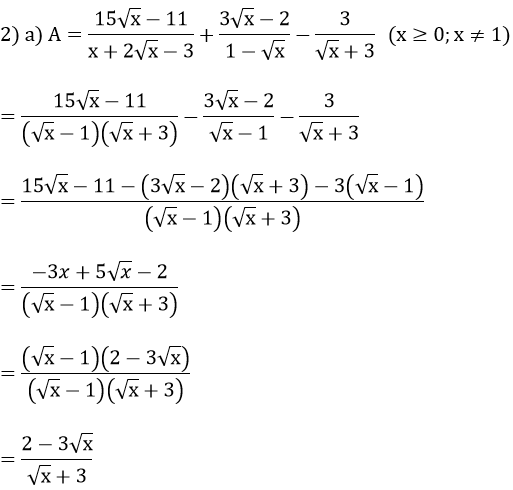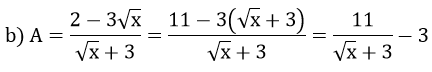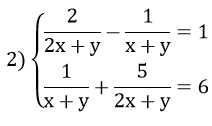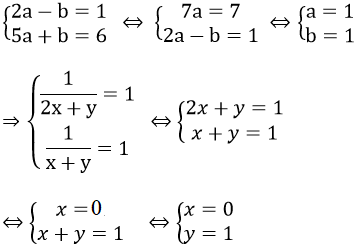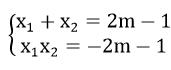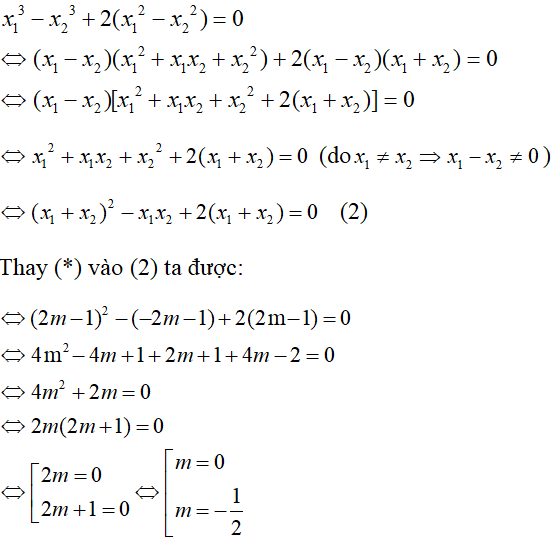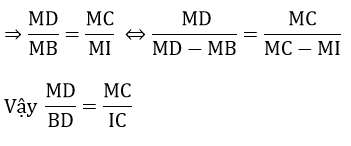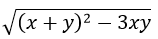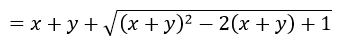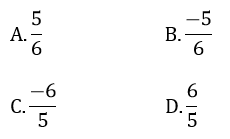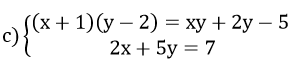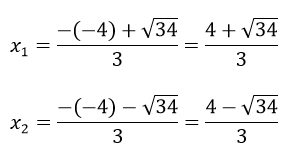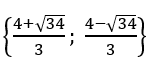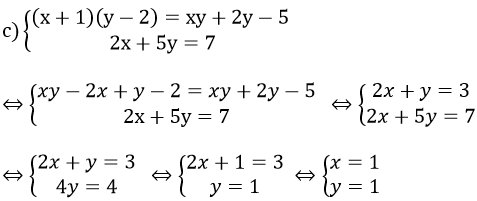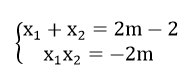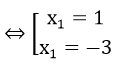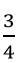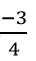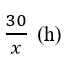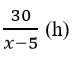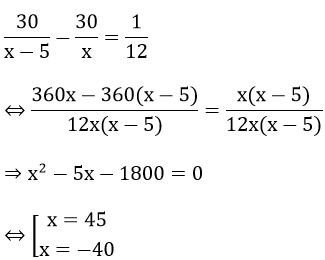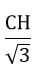Bộ đề thi vào lớp 10 môn Toán năm 2023 có đáp án (Trắc nghiệm - Tự luận)

---

Bộ đề thi vào lớp 10 môn Toán năm 2023 có đáp án (Trắc nghiệm - Tự luận)

Haylamdo biên soạn và sưu tầm Bộ đề thi vào lớp 10 môn Toán năm 2023 có đáp án (Trắc nghiệm - Tự luận) được các Thầy/Cô giáo nhiều năm kinh nghiệm biên soạn và tổng hợp chọn lọc từ đề thi môn Toán vào lớp 10 của các trường THPT trên cả nước sẽ giúp học sinh có kế hoạch ôn luyện từ đó đạt điểm cao trong kì thi tuyển sinh vào lớp 10 môn Toán.

Sở Giáo dục và Đào tạo .....

Trường THPT ....

Kì thi tuyển sinh vào lớp 10

Năm học 2023

Môn: Toán

Thời gian làm bài: 120 phút

(Đề thi số 1)

Phần I. Trắc nghiệm (2 điểm)

Câu 1: Điều kiện xác định của biểu thức 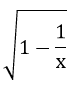là:

A.x ≠ 0    B.x ≥ 1    C.x ≥ 1 hoặc x < 0    D.0 < x ≤ 1

Câu 2: Đường thẳng 2x + 3y = 5 đi qua điểm nào trong các điểm sau đây

A. ( 1; -1)    B. ( 2; -3)    C. ( -1; 1)     D. (- 2; 3)

Câu 3: Cho phương trình x – 2y = 2 (1). Phương trình nào trong các phương trình sau đây kết hợp với (1) để được phương trình vô số nghiệm

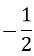
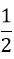
A.x + y = -1    B. x - y = -1

C.2x - 3y = 3   D.2x - 4y = -4

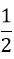
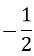
Câu 4: Tọa độ giao điểm của (P) y = x² và đường thẳng (d) y = + 3

A. (2; 2)   B. ( 2; 2) và (0; 0)

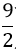
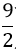
C.(-3; )    D.(2; 2) và (-3; )

Câu 5: Giá trị của k để phương trình x² + 3x + 2k = 0 có 2 nghiệm trái dấu là:

A. k > 0   B. k < 0   C. k > 2    D. k < 2

Câu 6: Cho tam giác ABC vuông tại A có AB : AC = 3 : 4 và đường cao AH bằng 9 cm. Khi đó độ dài đoạn thẳng HC bằng:

A. 12 cm    B. 9 cm     C. 6 cm    D. 15 cm

Câu 7: Cho hai đường tròn (O; 3cm) và (O; 4cm) có OO' = 5 cm. Vị trí tương đối của 2 đường tròn là:

A. Hai đường tròn tiếp xúc ngoài với nhau

B. Hai đường tròn tiếp xúc trong với nhau

C. Hai đường tròn không giao nhau

D. Hai đường tròn cắt nhau

Câu 8: Thể tích hình cầu thay đổi như thế nào nếu bán kính hình cầu tăng gấp 2 lần

A. Tăng gấp 16 lần     B. Tăng gấp 8 lần

C. Tăng gấp 4 lần     D. Tăng gấp 2 lần

Phần II. Tự luận

Bài 1: (2 điểm)

1) Thu gọn biểu thức

2) giải phương trình và hệ phương trình sau:

a) 3x² + 5x - 8 = 0

b) (x² + 5)² = 3(x² + 5) + 4

Bài 2: (1,5 điểm) Trong mặt phẳng tọa độ Oxy cho Parabol (P) : y = x² và đường thẳng (d) :

y = 2mx – 2m + 1

a) Với m = -1 , hãy vẽ 2 đồ thị hàm số trên cùng một hệ trục tọa độ

b) Tìm m để (d) và (P) cắt nhau tại 2 điểm phân biệt : A (x₁; y₁ );B(x₂; y₂) sao cho tổng các tung độ của hai giao điểm bằng 2 .

Bài 3: (1 điểm) Rút gọn biểu thức sau:

Tìm x để A < 0

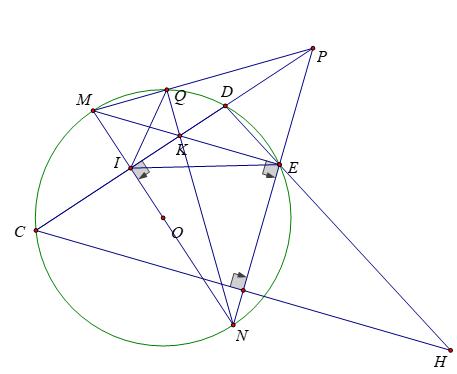
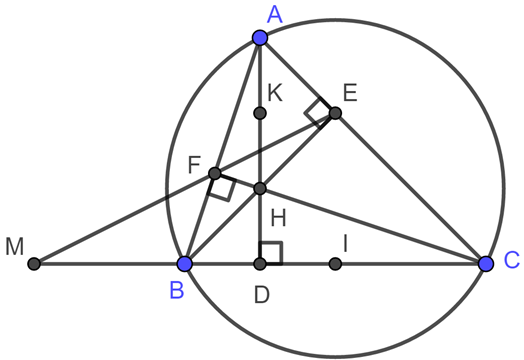
Bài 4: (3,5 điểm) Cho đường tròn (O) có dây cung CD cố định. Gọi M là điểm nằm chính giữa cung nhỏ CD. Đường kính MN của đường tròn (O) cắt dây CD tại I. Lấy điểm E bất kỳ trên cung lớn CD, (E khác C,D,N); ME cắt CD tại K. Các đường thẳng NE và CD cắt nhau tại P.

a) Chứng minh rằng :Tứ giác IKEN nội tiếp

b) Chứng minh: EI.MN = NK.ME

c) NK cắt MP tại Q. Chứng minh: IK là phân giác của góc EIQ

d) Từ C vẽ đường thẳng vuông góc với EN cắt đường thẳng DE tại H. Chứng minh khi E di động trên cung lớn CD (E khác C, D, N) thì H luôn chạy trên một đường cố định.

Phần I. Trắc nghiệm

1.C	2.D	3.A	4.D
5.B	6.A	7.D	8.B

Phần II. Tự luận

Bài 1:

2) a) 3x² + 5x - 8 = 0

Δ = 5² - 4.3.(-8) = 121 => √Δ = 11

Vậy phương trình đã cho có tập nghiệm là S =

b) (x² + 3)² = 3(x² + 3) + 4

Đặt x² + 3 = t (t ≥ 3), phương trình đã cho trở thành

t² - 3t - 4 = 0

Δ = 3² - 4.(-4) = 25> 0

Phương trình có 2 nghiệm phân biệt :

Do t ≥ 3 nên t = 4

Với t = 4, ta có: x² + 3 = 4 ⇔ x² = 1 ⇔ x = ±1

Vậy phương trình đã cho có 2 nghiệm x = ± 1

Bài 2:

Trong mặt phẳng tọa độ Oxy cho Parabol (P) : y = x² và đường thẳng (d) :

y = 2mx – 2m + 1

a) Với m = 1; (d): y = 2x – 1

Bảng giá trị

x	0	1
y = 2x – 1	-1	1

(P) : y = x²

Bảng giá trị

x	-2	-1	0	1	2
y = x2	4	1	0	1	4

Đồ thị hàm số y = x² là đường parabol nằm phía trên trục hoành, nhận Oy làm trục đối xứng và nhận điểm O(0; 0) là đỉnh và điểm thấp nhất

b) cho Parabol (P) : y = x2 và đường thẳng (d) :

y = 2mx – 2m + 1

Phương trình hoành độ giao điểm của (P) và (d) là:

x² = 2mx - 2m + 1

⇔ x² - 2mx + 2m - 1 = 0

Δ' = m² - (2m - 1)=(m - 1)²

(d) và (P) cắt nhau tại 2 điểm phân biệt khi và chỉ khi phương trình hoành độ giao điểm có 2 nghiệm phân biệt

⇔ Δ' > 0 ⇔ (m - 1)² > 0 ⇔ m ≠ 1

Khi đó (d) cắt (P) tại 2 điểm A(x₁, 2mx₁ – 2m + 1) ; B ( x₂, 2mx₂ – 2m + 1)

Theo định lí Vi-et ta có: x₁ + x₂ = 2m

Từ giả thiết đề bài, tổng các tung độ giao điểm bằng 2 nên ta có:

2mx₁ – 2m + 1 + 2mx₂ – 2m + 1 = 2

⇔ 2m (x₁ + x₂) – 4m + 2 = 2

⇔ 4m² - 4m = 0 ⇔ 4m(m - 1) = 0

Đối chiếu với điều kiện m ≠ 1, thì m = 0 thỏa mãn.

Bài 3:

A > 0 ⇔ 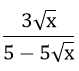> 0 ⇔ 5 - 5√x > 0 ⇔ √x < 1 ⇔ x < 1

Vậy A > 0 khi 0 < x < 1

Bài 4:

a) Do M là điểm chính giữa cung CD nên OM ⊥ CD

=> ∠KIN = 90^o

Xét tứ giác IKEN có:

∠KIN = 90^o

∠KEN = 90^o (góc nội tiếp chắn nửa đường tròn)

=> ∠KIN + ∠KEN = 180^o

=> Tứ giác IKEN là tứ giác nội tiếp

b) Xét ΔMEI và ΔMNK có:

∠NME là góc chung

∠IEM = ∠MNK ( 2 góc nội tiếp cùng chắn cung IK)

=> ΔMEI ∼ ΔMNK (g.g)

=>EI.MN = NK.ME

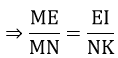
c) Xét tam giác MNP có:

ME ⊥ NP; PI ⊥ MN

ME giao PI tại K

=> K là trực tâm của tam giác MNP

=> ∠NQP = 90^o

Xét tứ giác NIQP có:

∠NQP = 90^o

∠NIP = 90^o

=> 2 đỉnh Q, I cùng nhìn cạnh NP dưới 1 góc bằng nhau

=> tứ giác NIQP là tứ giác nội tiếp

=> ∠QIP = ∠QNP (2 góc nội tiếp cùng chắn cung PQ)(1)

Mặt khác IKEN là tứ giác nội tiếp

=> ∠KIE = ∠KNE (2 góc nội tiếp cùng chắn cung KE)(2)

Từ (1) và (2)

=> ∠QIP = ∠KIE

=> IE là tia phân giác của ∠QIE

d) Ta có:

Mà ∠DEM = ∠MEC (2 góc nội tiếp chắn 2 cung bằng nhau)

=> ∠EHC = ∠ECH => ΔEHC cân tại E

=> EN là đường trung trực của CH

Xét đường tròn (O) có: Đường kính OM vuông góc với dây CD tại I

=> NI là đường trung trực của CD => NC = ND

EN là đường trung trực của CH => NC = NH

=> N là tâm đường tròn ngoại tiếp tam giác DCH

=> H ∈ (N, NC)

Mà N, C cố định => H thuộc đường tròn cố định

Sở Giáo dục và Đào tạo .....

Trường THPT ....

Kì thi tuyển sinh vào lớp 10

Năm học 2023

Môn: Toán

Thời gian làm bài: 120 phút

(Đề thi số 2)

Phần I. Trắc nghiệm (2 điểm)

Câu 1: Trong các hàm số sau, hàm số nào là hàm số bậc nhất

A. y = 1 -    B. y = - 2x

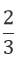
C. y = x² + 1     D. y = √x + 1

Câu 2: Hệ phương trình 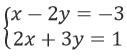có nghiệm là:

A. ( 1 ; 2)     B. ( 3; 3)    C. ( -1; 1)     D. (-3; 0)

Câu 3: Cho hàm số y = - x². Kết luận nào sau đây là đúng:

A. y = 0 là giá trị lớn nhất của hàm số

B. y = 0 là giá trị nhỏ nhất của hàm số

C. Không xác định được giá trị lớn nhất của hàm số trên

D. Xác định được giá trị nhỏ nhất của hàm số trên

Câu 4: Cho phương trình bậc hai x² – 2( 2m +1)x + 2m = 0. Hệ số b' của phương trình là:

A. m + 1    B. m    C. 2m +1     D. – (2m +1)

Câu 5: Phương trình x² + 2x + a – 2 = 0 vô nghiệm khi:

A. a > 3   B. a < 3     C. a ≥ 3     D. a ≤ 3

Câu 6: Đường tròn là hình:

A. Không có trục đối xứng    B. Có một trục đối xứng

C. Có hai trục đối xứng    D. Có vô số trục đối xứng

Câu 7: Tam giác ABC vuông tại A, có AB = 18 cm, AC = 24 cm. Bán kính đường tròn ngoại tiếp tam giác đó bằng

A. 30 cm    B. 20 cm     C. 15 cm   D. 10 cm

Câu 8: Một hình trụ có chiều cao bằng 8 cm và bán kính đáy bằng 4 cm thì diện tích toàn phần bằng:

A.336πcm²   B.96πcm²   C.168πcm²    D.48πcm²

Phần II. Tự luận

Bài 1: (1,5 điểm)

1) Thực hiện phép tính: 4√24 - 3√54 + 5√6 - √150

2) Cho biểu thức

a) Rút gọn A

b) Tìm x nguyên để A nguyên

Bài 2: (1,5 điểm)

1) Cho hàm số: y = - 2x + 3 có đồ thị (d₁) và hàm số y = x – 1 có đồ thị (d₂). Xác định hệ số a và b biết đường thẳng (d₃) y = ax + b song song với (d₂) và cắt (d₁) tại điểm nằm trên trục tung.

2) giải hệ phương trình sau:

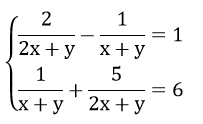
Bài 3: (1 điểm) Cho phương trình ( m là tham số)

x² - (2m - 1)x - 2m - 1 = 0 (1)

a) Chứng tỏ phương trình (1) luôn có 2 nghiệm phân biệt với mọi m

b) Tìm m để phương trình (1) có hai nghiệm x₁, x₂ thỏa mãn

x₁³ - x₂³ + 2(x₁² - x₂² ) = 0

Bài 4: (3,5 điểm) Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O) có các đường cao AD, BE, CF, trực tâm H. Gọi I, K lần lượt là các trung điểm của các đoạn BC và AH

a) Chứng minh tứ giác BFEC và BFHD nội tiếp

b) Chứng minh DH. DA = DB. DC

c) Chứng minh 5 điểm E, K, F, D, I thuộc một đường tròn

d) Đường thẳng EF cắt BC tại M. Chứng minh

Bài 5: (0,5 điểm) Cho x, y thỏa mãn 0 < x < 1; 0 < y < 1 và 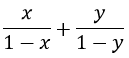= 1

Tìm giá trị của biểu thức

P = x + y +

Phần I. Trắc nghiệm

1.B	2.C	3.A	4.D
5.A	6.D	7.C	8.B

Phần II. Tự luận

Bài 1:

1) 4√24 - 3√54 + 5√6 - √150

= 4√4.6 - 3.√9.6 + 5√6 - √25.6

= 8√6 - 9√6 + 5√6 - 5√6

= -√6

A nguyên ⇔ 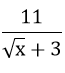nguyên ⇔ √x + 3 là ước của 11

⇔ √x + 3 ∈ {±1 ; ±11}

Ta có bảng sau:

√x + 3	-11	-1	1	11
√x	-14	-4	-2	8
x	X	X	X	64

Vậy x = 64 thì A nhận giá trị nguyên.

Bài 2:

1): y = - 2x + 3 có đồ thị (d₁); hàm số y = x – 1 có đồ thị (d₂).

Đường thẳng (d₃) y = ax + b song song với (d₂) nên a =1

(d₃) : y = x + b

Đường thẳng (d₁) y = - 2x + 3 cắt trục tung tại điểm (0; 3)

(d₃) cắt (d₁) tại điểm nằm trên trục tung nên (d₃) đi qua điểm (0; 3)

=> 3 = 0 + b => b = 3

Vậy phương trình đường thẳng (d₃) là y = x + 3

ĐKXĐ: x + y ≠ 0; 2x + y ≠ 0

Đặt 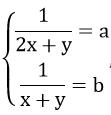, hệ phương trình trở thành:

Vậy hệ phương trình đã cho có nghiệm (x, y) = (0; 1)

Bài 3:

x² - (2m - 1)x - 2m - 1 = 0 (1)

a) Δ = (2m - 1)² - 4(-2m - 1)

= 4m² - 4m + 1 + 8m + 4 = 4m² + 4m + 1 + 4

= (2m + 1)² + 4 > 0 ∀m

Vậy phương trình luôn có 2 nghiệm phân biệt với mọi m

b) Gọi x₁, x₂ là 2 nghiệm của phương trình (1)

Theo định lí Vi-ét ta có:

Vậy với m = 0 hoặc 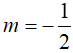thì pt (1) có hai nghiệm thỏa mãn yêu cầu của đề bài

Bài 4:

a) Xét tứ giác BFEC có:

∠BFC = 90^o (CF là đường cao)

∠BEC = 90^o (BE là đường cao)

=> 2 đỉnh E và F cùng nhìn cạnh BC dưới 2 góc bằng nhau

=> Tứ giác BFEC là tứ giác nội tiếp

Xét tứ giác BFHD có:

∠BFH = 90^o (CF là đường cao)

∠BDH = 90^o (AD là đường cao)

=> ∠BFH + ∠BDH = 180^o

=> Tứ giác BFHD là tứ giác nội tiếp

b) Xét ΔDHC và ΔDBA có:

∠HDC = ∠BDA = 90^o

∠DHC = ∠DBA ( cùng bù với góc ∠FHD )

=> ΔDHC ∼ ΔDBA (g.g)

=> DH.DA = DC.DB

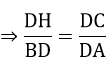
c) Ta có: ∠KDI = 90^o (AD là đường cao)

=> D thuộc đường tròn đường kính KI (1)

Tam giác AFH vuông tại F có FK là trung tuyến nên KF = KH

Do đó ΔKFH cân tại K => ∠KFH = ∠KHF

Mà ∠KHF = ∠CHD (đối đỉnh) => ∠KFH = ∠CHD

Tương tự ΔICF cân tại C (do IF = IC) => ∠IFC = ∠ICF

Từ đó: ∠KFI = ∠KFH + ∠IFC = ∠CHD + ∠ICF = 90^o (ΔDHC vuông tại D)

=> F thuộc đường tròn đường kính KI (2)

Chứng minh tương tự ∠KEI = 90^o nên E thuộc đường tròn đường kính KI (3)

Từ (1), (2), (3): 5 điểm K, F, D, I, E thuộc đường tròn đường kính KI

d) Xét ΔMFB và ΔMCE có:

=> ΔMFB ∼ ΔMCE

=> MF.ME = MB.MC

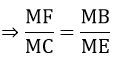
Chứng minh tương tự: ME. MF = MD. MI

Từ đó: MB.MC = MD. MI

Bài 5:

Từ giả thiết 0 < x < 1; 0 < y < 1, ta có:

Thay 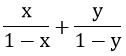= 1 => 2x + 2y - 1 = 3xy vào biểu thức P

P = x + y +

= x + y + = x + y + 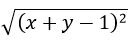|x + y - 1|

= x + y + 1 - (x + y) (do x + y < 1)

= 1.

Sở Giáo dục và Đào tạo .....

Trường THPT ....

Kì thi tuyển sinh vào lớp 10

Năm học 2023

Môn: Toán

Thời gian làm bài: 120 phút

(Đề thi số 3)

Phần I. Trắc nghiệm (2 điểm)

Câu 1: Trong các đường thẳng sau đây, đường thẳng nào đi qua điểm A (1; 3):

A. x – y = 3     B. 2x + y =5

C. 2x – y = 3    D. x + y = 5

Câu 2: Điều kiện xác định của biểu thức 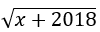là:

A. x = -2018     B. x ≠ -2018

C. x ≥ -2018     D. x ≤ -2018

Câu 3: Tìm m để 2 đường thẳng sau cắt nhau tại 1 điểm y = (2m – 1)x + 7 và y = 3x – 5

A. m = 2     B. m ≠ 2    C. m ≥ 2    D. m ≤ 2

Câu 4: Tìm giá trị của a để đồ thị hàm số y = ax² đi qua điểm (1; - 4)

A. a = - 2     B. a = 2     C. a = 4    D. a = - 4

Câu 5: Biết phương trình x² + bx – 2b = 0 có một nghiệm x = -3. Tìm nghiệm còn lại của phương trình:

Câu 6: Trong các nhận xét sau, nhận xét đúng là:

A. Hai cung bằng nhau thì có số đo bằng nhau

B. Hai cung có số đo bằng nhau thì bằng nhau

C. Cả a, b đều đúng

D. Cả a và b đều sai

Câu 7: Tính diện tích hình quạt có bán kính 6cm, độ dài cung là 5π cm

A. 10π cm²     B. 20π cm²    C.30π cm²    D. 15Bπ cm²

Câu 8: Tính diện tích toàn phần của hình nón có bán kính đáy 5 cm và độ dài đường sinh là 7 cm:

A. 35π cm²   B. 45π cm²    C. 52π cm²   D. 60π cm²

Phần II. Tự luận

Bài 1: (1,5 điểm) Giải các phương trình và hệ phương trình:

a) √5x - 2√5 = 0

b)3x² - 8x - 6 = 0

Bài 2: (2 điểm)

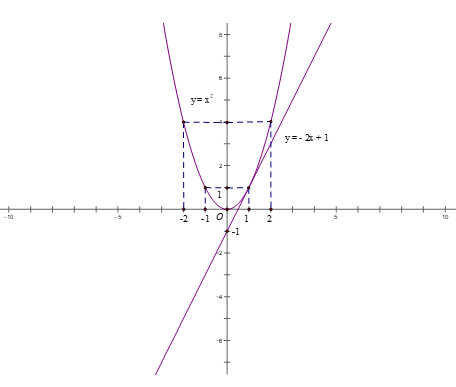
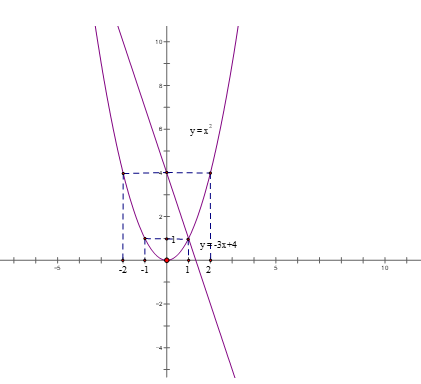
1) Cho 2 hàm số (P): y = 2x² và (d): y = -3x + 4

a) Vẽ 2 đồ thị trên cùng một mặt phẳng tọa độ Oxy

b) Tìm tọa độ giao điểm của 2 đồ thị trên bằng phép tính.

2) Cho phương trình x² – 2(m – 1)x – 2m = 0.

Chứng minh rằng phương trình luôn có 2 nghiệm phân biệt với mọi m. Gọi 2 nghiệm của phương trình là x1; x2, tìm tất cả giá trị của m sao cho x₁² + x₁ - x₂ = 5 - 2m

Bài 3: (1 điểm) Hai xe máy cùng xuất phát một lúc từ địa điểm A đến địa điểm B cách nhau 30 km. Xe thứ nhất chạy nhanh hơn xe thứ hai 5km/h nên đến B sớm hơn 5 phút. Tính vận tốc mỗi xe

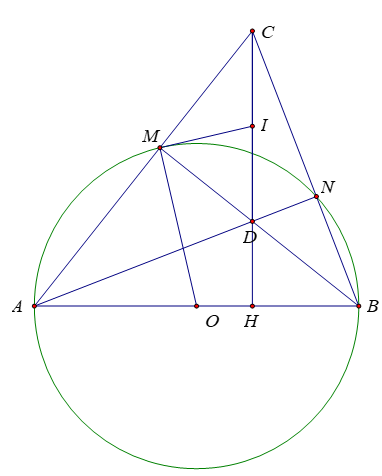
Bài 4: (3,5 điểm) Trên đường tròn (O; R) đường kính AB lấy 2 điểm M, N theo thứ tự A, M, N, B ( hai điểm M, N khác 2 điểm A và B). Các đường thẳng AM và BN cắt nhau tại C, AN và BM cắt nhau tại D

a) Chứng minh tứ giác MCND nội tiếp. Xác định tâm I đường tròn ngoại tiếp tứ giác

b) Gọi H là giao điểm của CD và AB. Chứng minh rằng:

BN.BC = BH.BAv

c) Tính ∠IMO

d) Cho biết ∠BAM = 45^o; ∠BAN = 30^o. Tính theo R diện tích của tam giác ABC

Phần I. Trắc nghiệm

1.B	2.C	3.B	4.A
5.D	6.A	7.C	8.D

Phần II. Tự luận

Bài 1:

a) √5x - 2√5 = 0

⇔ √5x = 2√5

⇔ x = 2

Vậy phương trình có nghiệm x = 2.

b)3x² - 8x - 6 = 0

Δ' = (-4)² - 3.(-6) = 34 > 0

Phương trình có 2 nghiệm phân biệt

Vậy phương trình có tập nghiệm là S =

Vậy hệ phương trình đã cho có nghiệm (x; y) = (1; 1)

Bài 2:

1) Cho 2 hàm số (P): y = x² và (d): y = -3x + 4

Xét hàm số: y = 2x²

Bảng giá trị

x	-2	-1	0	1	2
y = 2x2	4	1	0	1	4

Đồ thị hàm số (P): y = x² là đường parabol nằm phía trên trục hoành, nhận trục Oy là trục đối xứng và nhận đỉnh O (0;0) làm điểm thấp nhất

Xét hàm số y = -3x + 4

Bảng giá trị

x	0	1
y = -3x + 4	4	1

b) phương trình hoành độ giao điểm của (P) và (d) là

x² = - 3x + 4 ⇔ x² + 3x - 4 = 0

=> phương trình có nghiệm x = 1 và x = - 4 ( do phương trình có dạng a + b + c =0)

Với x = 1 thì y = 1

Với x = - 4 thì y = 16

Vậy tọa độ giao điểm của (P) và (d) là (1; 1 ) và (-4; 16)

2) x² – 2(m – 1)x – 2m = 0.

Δ'= (m-1)² - (-2m) = m² + 1 > 0 ∀m

Vậy phương trình luôn có 2 nghiệm phân biệt với mọi m

Theo định lí Vi- ét ta có:

⇔ x₁² + x₁ - x₂ = 3 - (2m - 2)

⇔ x₁² + x₁ - x₂ = 3 - x₁ - x₂

⇔ x₁² + 2x₁ - 3 = 0

Với x₁ = 1 thay vào phương trình ban đầu tìm được m =

Với x₁ = -3 thay vào phương trình ban đầu, tìm đc m =

Vậy với m = 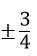thì phương trình có 2 nghiệm thỏa mãn yêu cầu đề bài.

Bài 3:

Gọi vận tốc xe thứ nhất là x ( km/h) (x > 5)

Vận tốc xe thứ hai là x – 5 (km/h)

Thời gian đi của xe thứ nhất là:

Thời gian đi của xe thứ hai là

Do xe thứ nhất đến B sớm hơn xe thứ hai 5' = 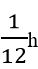nên ta có phương trình

Vậy vận tốc của xe thứ nhất là 45 km/h

Vận tốc xe thứ hai là 40 km/h

Bài 4:

a) Ta có:

∠AMB = 90^o (góc nội tiếp chắn nửa đường tròn)

=> ∠DMC = 90^o

∠ANB = 90^o (góc nội tiếp chắn nửa đường tròn)

=> ∠DNC = 90^o

Xét tứ giác MCND có:

∠DMC + ∠DNC = 90^o + 90^o = 180^o

=> Tứ giác MCDN là tứ giác nội tiếp

Do ∠DMC = 90^o nên DC là đường kính đường tròn ngoại tiếp tứ giác MCDN

Do đó tâm I của đường tròn ngoại tiếp tứ giác là trung điểm I của DC

b) Xét tam giác CAB có:

AN ⊥ BC

BM ⊥ AC

AN giao với BM tại H

=> H là trực tâm của tam giác CAB

=> CH ⊥ BA

Xét ΔCHB và ΔBNA có:

∠CBA là góc chung

∠CHB = ∠ANB = 90^o

=>ΔCHB ∼ ΔANB

=> BN.BC = BA.BH

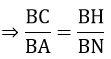
c) Xét tam giác HDB vuông tại H có:

∠BDH + ∠DBH = 90^o (1)

Xét tam giác IDM cân tại I (ID = IM )

=> ∠IMD = ∠IDM

Mà ∠IDM = ∠BDH (đối đỉnh)

=> ∠IMD = ∠BDH (2)

Mặt khác tam giác OBM cân tại O ( OB = OM)

=> ∠OMB = ∠DBH (3)

Từ (1); (2) và (3)

=> ∠IMD + ∠OMB = ∠BDH + ∠DBH = 90^o

=> ∠IMO = 90^o

d) Xét tam giác BAN vuông tại N có:

∠NAB = 30^o => ∠NBA = 60^o

Xét tam giác CHB vuông tại H có ∠NBA = 60^o

=> BH = CH.cot60^o =

Lại có: Tam giác CHA vuông tại H có ∠CAH = 45^o

=> Tam giác CHA vuông cân tại H => CH = HA

Ta có:

AB = HA + HB = CH +

= 2R => CH = R√3(√3-1)

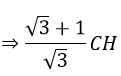
Diện tích tam giác ABC là:

S_ABC = CH.AB = .R√3(√3-1).2R = R².√3(√3-1) (dvdt)