Người ta muốn chế tạo một chiếc hộp hình chữ nhật có thể tích 800 cm^3

Người ta muốn chế tạo một chiếc hộp hình chữ nhật có thể tích 800 cm với yêu cầu dùng ít vật liệu nhất.

Giải SBT Toán 12 Chân trời sáng tạo Bài tập cuối chương 1

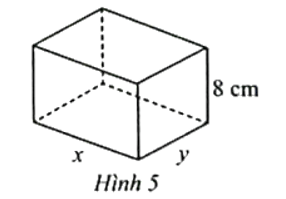
Bài 8 trang 37 SBT Toán 12 Tập 1: Người ta muốn chế tạo một chiếc hộp hình chữ nhật có thể tích 800 cm³ với yêu cầu dùng ít vật liệu nhất.

Chiều cao hộp là 8 cm, các kích thước khác là x (cm), y (cm) với x > 0 và y > 0.

a) Chứng tỏ rằng y = $\frac{100}{x}$ .

b) Tìm diện tích toàn phần S(x) của chiếc hộp theo x.

c) Khảo sát hàm số S(x) trên khoảng (0; +∞).

d) Tìm kích thước của hộp để tiết kiệm vật liệu nhất. (Làm tròn kết quả đến hàng đơn vị của mi-li-mét).

Lời giải:

a) Ta có: V = 800 = 8xy ⇒ y = $\frac{800}{8 x} = \frac{100}{x}$ .

b) Diện tích toàn phần của chiếc hộp là:

S(x) = 2(x + y).8 + 2xy = 16 $(x + \frac{100}{x})$ + 2x. $\frac{100}{x}$ = 16x + $\frac{1600}{x}$ + 200.

c) S(x) = 16x + $\frac{1600}{x}$ + 200, với x > 0.

S'(x) = 16 – $\frac{1600}{x^{2}}$

S'(x) = 0 ⇔ x² = 100 ⇔ x = 10.

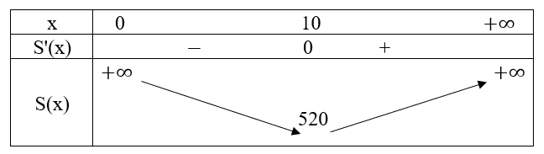
Bảng biến thiên:

Người ta muốn chế tạo một chiếc hộp hình chữ nhật có thể tích 800 cm^3

Hàm số đồng biến trên (10; +∞), hàm số nghịch biến trên khoảng (0; 10).

d) Khi x = 10 thì hàm số S(x) đạt giá trị nhỏ nhất và S(10) = 520.

Lúc này, y = $\frac{100}{x} = \frac{100}{10}$ = 10, nghĩa là khi làm đáy hộp là hình vuông có cạnh bằng 10 cm thì sẽ tiết kiệm vật liệu nhất.

Lời giải SBT Toán 12 Bài tập cuối chương 1 hay khác: