Cho hàm số y = (x^2 +mx + 1)/(x+m). Hàm số đạt cực đại tại x = 2 khi

Giải sách bài tập Toán 12 Bài tập cuối chương 1 - Kết nối tri thức

Bài 1.55 trang 34 SBT Toán 12 Tập 1: Cho hàm số $y = \frac{x^{2} + m x + 1}{x + m}$ . Hàm số đạt cực đại tại x = 2 khi

A. m = −1.

B. m = −3.

C. m ∈ {−3; −1}.

D. m ∈∅.

Lời giải:

Đáp án đúng là: A

Tập xác định: D = ℝ\{−m}.

Ta có: y' = $\frac{(x + m + 1) (x + m - 1)}{{(x + m)}^{2}}$

y' = 0 ⇔ $\frac{(x + m + 1) (x + m - 1)}{{(x + m)}^{2}}$ = 0 ⇔ x = −m – 1

hoặc x = 1 – m.

Nhận thấy, với mọi m luôn có −m – 1 < 1 – m.

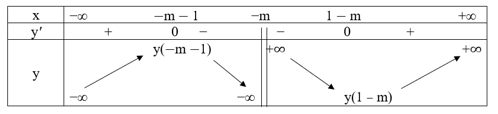
Ta có bảng biến thiên như sau:

Cho hàm số y = (x^2 +mx + 1)/(x+m). Hàm số đạt cực đại tại x = 2 khi

Để hàm số đạt cực đại tại x = 2 thì −m – 1 = 2 hay m = −1.

Vậy m = −1.

Lời giải Sách bài tập Toán lớp 12 Bài tập cuối chương 1 hay khác: